
湖北省2009届高三数学月考模拟分类汇编――集合与常用逻辑用语
1、(2009湖北八校第一次月考)与集合 相等的集合是( )
相等的集合是( )
A.  B.
B.
 C.
C.  D.
D.
C
2、(2009湖北八校第一次月考)设 ,
, .若
.若 是
是 的必要而不充分条件,则实数
的必要而不充分条件,则实数 的取值范围是( )
的取值范围是( )
A. B.
B. C.
C. ∪
∪ D.
D. ∪
∪
A
3、(2009黄冈市期末)已知集合M={0,1,2},N={x|x=
A.{0 } B.{0,1} C.{1,2} D.{0,2}
D
4、(2009蕲春一中第四次阶段考)全集 ,集合
,集合 ,
, 则
则 w.w.w.k.s.5.u.c.o.m
w.w.w.k.s.5.u.c.o.m
A、 B、
B、 C、
C、 D、
D、
B
5、(2009黄冈五所重点高中12月)已知集合M=  ,集合
,集合 为自然对数的底数),则
为自然对数的底数),则 =
=
A. B.
B. C.
C. D.
D.
C
6、(2009荆州中学期末)已知命题 :不等式
:不等式 的解集为R;命题
的解集为R;命题 :
: 为减函数. 则
为减函数. 则 是
是 成立的( )
成立的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
B
7、(2009随州曾都一中第一次月考)设 ,则下列关系正确的是
,则下列关系正确的是
A. B.
B. C.
C. D.
D.
D
8、(2009随州曾都一中第一次月考)集合 ,
, ,则“
,则“ ”是“
”是“ ”的
”的
A.充分非必要条件 B.必要非充分条件
C.充分必要条件 D.既非充分也非必要条件
B
9、(2009武汉市教科院第一次调考)
已知集合 = ( )
= ( )
A. B.
B. C.
C. D.
D.
A
10、(2009武汉市教科院第一次调考) “p或q是假命题”是“非p为真命题”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D 既不充分又不必要条件
既不充分又不必要条件
A
11、(2009武昌区1月调考)若 ,则“
,则“ ”是“
”是“ ”的 ( )
”的 ( )
A.充分而不必要条件 B.必要而不充分条件
C.充分必要条件 D.既不充分也不必要条件
D
12、(2009浠水一中模拟)
设集合 的集合C的个数是
的集合C的个数是
A.0 B.
C
13、(2009宜昌一中12月月考)已知命题p:不等式|x|+|x-1|>m的解集为R,命题q:f(x)=-(5 是减函数,则p是q的
是减函数,则p是q的
A.充分非必要条件 B.必要非充分条件
C.充要条件 D.既不充分也不必要条件
A
14、(2009随州曾都一中第一次月考)
已知集合
(1)当m=3时,求 ;
;
(2)若 求实数m的值.
求实数m的值.
解: ,(1)当
,(1)当
则  =
=

 =
= 6分
6分
(2)
 12分
12分
15、(2009荆州中学期末)设全集 ,集合
,集合 ,
, ,求
,求 .
.
解:当 时,原不等式变形为
时,原不等式变形为 ,解得
,解得

当 时,原不等式变形为
时,原不等式变形为 ,解得
,解得

当 时,原不等式变形为
时,原不等式变形为 ,解得
,解得

综上, ……………………………………………4分
……………………………………………4分
由 得
得 ;
;
当 时,
时, ;
; 时,
时,
∴ 在
在 单减,在
单减,在 单增。….8分
单增。….8分
∴ ,即
,即
∴ ……………………………………..12分
……………………………………..12分
 w.w.w.k.s.5.u.c.o.m
w.w.w.k.s.5.u.c.o.m
湖北省2009届高三数学月考模拟分类汇编――函数
一、选择题
1、(2009湖北八校第一次月考)设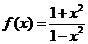 ,则
,则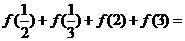 ( )
( )
A.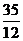 B.
B.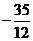 C.
C. 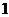 D.
D.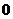
D
2、(2009黄冈市期末)设函数f(x)(x∈R)为奇函数,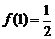 ,f(x+2)=f(x)+f(2),则f(5)=( )
,f(x+2)=f(x)+f(2),则f(5)=( )
A.0 B.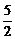 D.5
D.5
C
3、(2009黄冈五所重点高中12月)在函数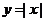 (
(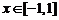 )的图象上有一点
)的图象上有一点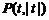 ,此函数与 x轴、直线x=-1
,此函数与 x轴、直线x=-1
及 x=t围成图形(如图阴影部分)的面积为S,则S与t的函数关系图可表示为

B
5、(2009荆州中学期末)已知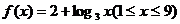 ,则函数
,则函数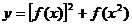 的最大值为( )
的最大值为( )
A.6 B.13 C.22 D.33
B
6、(2009随州曾都一中第一次月考)7.已知定义在R上的函数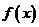 满足
满足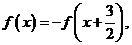 且
且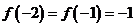 ,
, 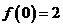 ,则
,则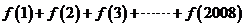 等于
等于
A.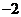 B.
B.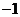 C.
C.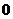 D.
D.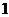
B
7、(2009随州曾都一中第一次月考)8.已知函数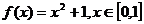 的反函数为
的反函数为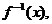 则函数
则函数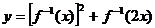 的值域是
的值域是
A.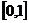 B.
B.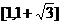 C.
C. D.
D.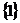
D
二、填空题
1、(2009黄冈市期末)定义在R上的函数f(x)满足:①偶函数;②对任意的x1,x2,都有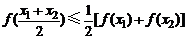 .请写出这样的一个函数f(x)________________.
.请写出这样的一个函数f(x)________________.
答案不唯一,如y=ax2+b(a>0)
2、(2009浠水一中模拟)13.已知函数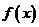 在R上可导,函数
在R上可导,函数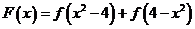 ,则
,则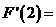 __ 0
__ 0
3、(2009浠水一中模拟)14.若函数在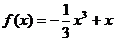 在
在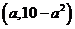 上有最大值,则实数
上有最大值,则实数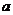 的取值范围为_
的取值范围为_ 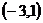
4、(2009浠水一中模拟)15.对于函数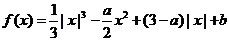 ,
,
(1)若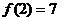 ,则
,则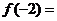 .
.
(2)若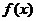 有六个不同的单调区间,则
有六个不同的单调区间,则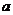 的取值范围为 .
的取值范围为 .
(1)7 (2)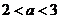
5、(2009咸宁市期末)设函数f(x)的图象关于点(1,2)对称,且存在反函数f―1(x),f(4)=0,则f―1(4)= 。
-2
三、解答题
1、(2009湖北八校第一次月考)已知函数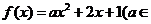 R).
R).
⑴若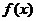 的图象与
的图象与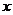 轴恰有一个公共点,求
轴恰有一个公共点,求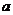 的值;
的值;
⑵若方程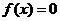 至少有一正根,求
至少有一正根,求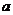 的范围.
的范围.
解:⑴若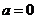 ,则
,则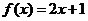 ,
,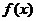 的图象与
的图象与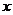 轴的交点为
轴的交点为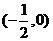 ,满足题意.
,满足题意.
若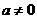 ,则依题意得:
,则依题意得: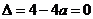 ,即
,即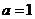 .
.
故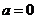 或
或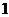 .
.
⑵显然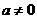 .
.
若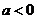 ,则由
,则由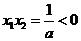 可知,方程
可知,方程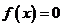 有一正一负两根,此时满足题意.
有一正一负两根,此时满足题意.
若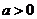 ,则
,则
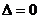 时,
时,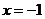 ,不满足题意.
,不满足题意.
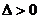 时,方程有两负根,也不满足题意.
时,方程有两负根,也不满足题意.
故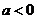 .
.
2、(2009黄冈市期末)已知函数f(x)=ax3+3x2-x+1在R上是减函数,求实数a的取值范围.
解:f′(x)=3ax2+6x-1,其判别式△=36+12a. (4分)
当a<-3时,有△<0,∴f′(x)<0,f(x)在R上是减函数; (6分)
当a=-3时,有△=0,此时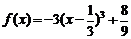 ,由于y=-x3是R上的减函数,所以f(x)在R上是减函数; (8分)
,由于y=-x3是R上的减函数,所以f(x)在R上是减函数; (8分)
当a>-3且a≠0时,有△>0,在R上存在区间A,使得当x∈A时,有f′(x)>0,此时f(x)在R上不是减函数.
当a=0时f(x)=3x2-x+1,不是R上的减函数, (10分)
综上所述,所求a的取值范围是(-∞,-3]. (12分)
3、(2009黄冈五所重点高中12月)已知函数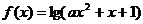
(Ⅰ)若函数的定义域为R,求a的取值范围.
(Ⅱ)若函数的值域为R,求a的取值范围.
解:令 设
设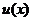 的值域为M.
的值域为M.
(Ⅰ)当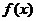 的定义域为R,有
的定义域为R,有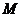
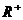 .
.
故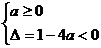
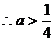 …………………………6分
…………………………6分
(Ⅱ)当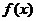 的值域为R,有
的值域为R,有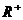
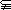
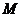
故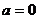 或
或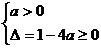
∴ 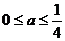 ………………………………………………12分
………………………………………………12分
4、(2009荆州中学期末)已知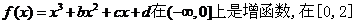 上是减函数,且
上是减函数,且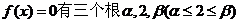

(1)求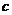 的值,并求出
的值,并求出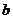 和
和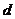 的取值范围;
的取值范围;
(2)求证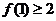 ;
;
(3)求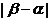 的取值范围,并写出当
的取值范围,并写出当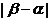 取最小值时的
取最小值时的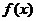 的解析式.
的解析式.
解:(1)
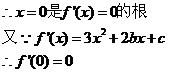
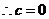
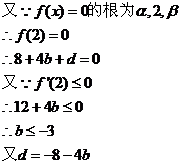
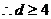 ………………………………………………………………………..4分
………………………………………………………………………..4分
(2)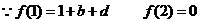
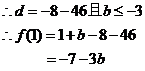
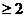 …………………………………………………………………8分
…………………………………………………………………8分
(3)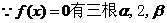
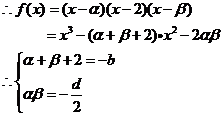
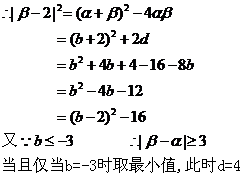
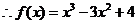 ……………………………………………………….14分
……………………………………………………….14分
5、(2009随州曾都一中第一次月考)已知二次函数 为偶函数,函数
为偶函数,函数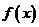 的图象与直线y=x相切.
的图象与直线y=x相切.
(1)求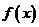 的解析式
的解析式
(2)若函数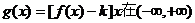 上是单调减函数,那么:
上是单调减函数,那么:
①求k的取值范围;
②是否存在区间[m,n](m<n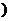 ,使得
,使得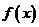 在区间[m,n]上的值域恰好为[km,kn]?若存在,请求出区间[m,n];若不存在,请说明理由.
在区间[m,n]上的值域恰好为[km,kn]?若存在,请求出区间[m,n];若不存在,请说明理由.
(1)∵f(x+1)为偶函数,∴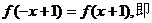
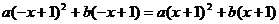 恒成立,即(2a+b)x=0恒成立,
恒成立,即(2a+b)x=0恒成立,
∴2a+b=0,∴b=-2a,∴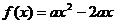
∵函数f(x)的图象与直线y=x相切,∴二次方程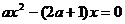 有两相等实数根,
有两相等实数根,
∴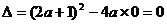 ,
,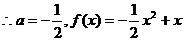 (5分)
(5分)
(2)①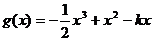 ,
,
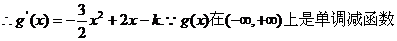
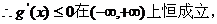
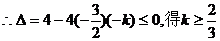
故k的取值范围为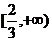 (8分)
(8分)
②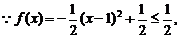
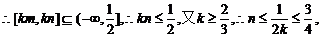
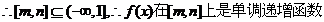
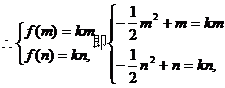 即
即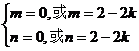
∵m<n,故当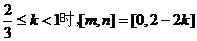 ;
;
当k>1时,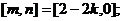
当k=1时,[m,n]不存在.(14分)
6、(2009武汉市教科院第一次调考)已知函数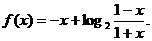
(1)求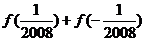 的值;
的值;
(2)当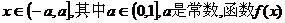 是否存在最小值?若存在,求出
是否存在最小值?若存在,求出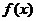 的最小值;若不存在,请说明理由。
的最小值;若不存在,请说明理由。
解:(1)由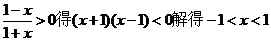
函数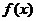 的定义域为(-1,1)
的定义域为(-1,1)
又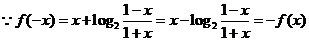
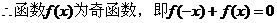
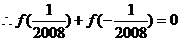 …………………………………(6分)
…………………………………(6分)
(2)任取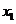 、
、
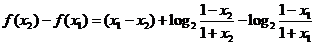
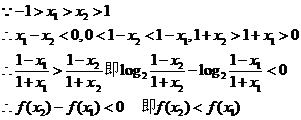
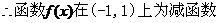
又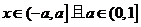
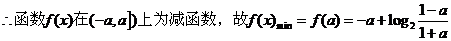 ……(13分)
……(13分)
7、(2009宜昌一中12月月考)已知二次函数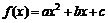 。
。
(1)若对任意x1,x2∈R,且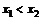 ,都有
,都有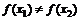 ,求证:关于x的方程
,求证:关于x的方程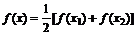 有两个不相等的实数根且必有一个根属于(
有两个不相等的实数根且必有一个根属于(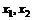 );
);
(2)若关于x的方程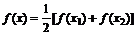 在(
在(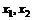 )的根为m,且
)的根为m,且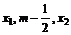 成等差数列,设函数f (x)的图象的对称轴方程为
成等差数列,设函数f (x)的图象的对称轴方程为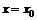 ,求证:
,求证: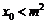 。
。
证明:(1)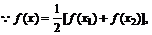
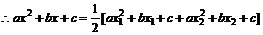 ,
,
整理得: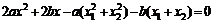 ,
2分
,
2分
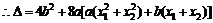
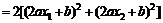
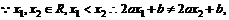 4分
4分
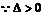 ,故方程有两个不相等的实数根。
6分
,故方程有两个不相等的实数根。
6分
令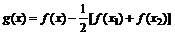 ,
7分
,
7分
则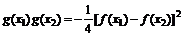 ,
,
又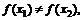 则
则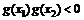 ,
,
故方程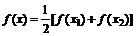 有一个根属于(x1,x2)
9分
有一个根属于(x1,x2)
9分
(2)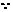 方程
方程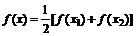 在
在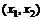 根为m,
根为m,
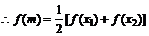 ,
,
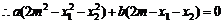 ,
10分
,
10分
∵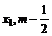 、x2成等差数列,则
、x2成等差数列,则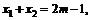 12分
12分
∴b=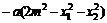 ,
,
故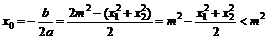 。
14分
。
14分
 w.w.w.k.s.5.u.c.o.m
w.w.w.k.s.5.u.c.o.m
湖北省2009届高三数学月考模拟分类汇编――不等式
一、选择题
1、(2009湖北八校第一次月考)若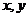 满足约束条件
满足约束条件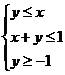 ,则目标函数
,则目标函数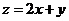 的最大值是 ( )
的最大值是 ( )
A.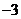 B.
B.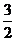 C.
C.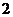 D.
D.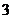
D
2、(2009黄冈市期末)10、若不等式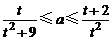 在t∈(0,2]上恒成立,则a的取值范围是( )
在t∈(0,2]上恒成立,则a的取值范围是( )

B
3、(2009黄冈五所重点高中12月)
设全集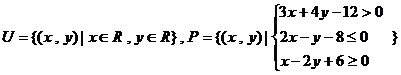 ,
,
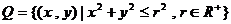 ,若
,若
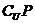 恒成立,则实数
恒成立,则实数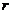 最大值是
最大值是
A. 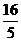 B.
B. 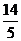 C.
C. 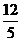 D.
D.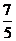
C
4、(2009黄冈五所重点高中12月)已知不等式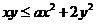 ,若对任意
,若对任意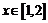 及
及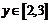 ,该不等式恒成立,则实数
,该不等式恒成立,则实数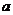 的范围是
的范围是
A.
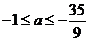
 B.
B.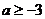 C.
C.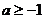 D.
D.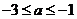
C
5、(2009随州曾都一中第一次月考)已知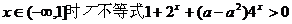 恒成立,则
恒成立,则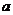 的取值范围是
的取值范围是
A.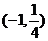 B.
B.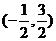 C.
C.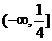 D.
D.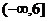
B
6、(2009武汉市教科院第一次调考)双曲线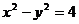 的两近渐近线和直线x=2围成一个三角形区域(含边界),则该区域可表示为 ( )
的两近渐近线和直线x=2围成一个三角形区域(含边界),则该区域可表示为 ( )
A.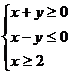 B.
B.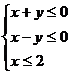 C.
C.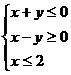 D.
D.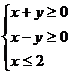
D
7、(2009武昌区1月调考)已知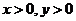 ,且
,且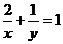 ,若
,若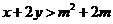 恒成立,
恒成立,
则实数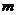 的取值范围是( )
的取值范围是( )
A.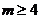 或
或 B.
B.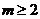 或
或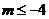 C.
C.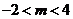 D.
D.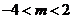
D
8、(2009浠水一中模拟)不等式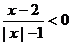 的解集为
的解集为
A.{x|1<x<2}
B.{x|x<2且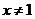 }
}
C.{x|-1<x<2且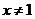 }
D. {x|x<-1或1<x<2}
}
D. {x|x<-1或1<x<2}
D
二、填空题
1、(2009湖北八校第一次月考)已知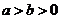 ,则
,则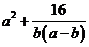 的最小值是
的最小值是
16
2、(2009黄冈市期末)11、已知不等式组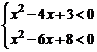 的解集是不等式2x2-9x+a<0的解集的子集,则实数a的取值范围是_________.
的解集是不等式2x2-9x+a<0的解集的子集,则实数a的取值范围是_________.
(-∞,9]
3、(2009武汉市教科院第一次调考)(文科)不等式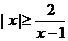 的解集为
。
的解集为
。
(理科)对于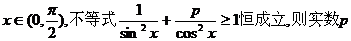 的取值范围是
的取值范围是

答案:(文)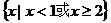 (理)
(理)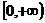
4、(2009咸宁市期末)若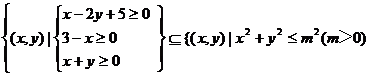 ,则实数m满足条件
,则实数m满足条件
。
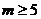
三、解答题
1、(2009黄冈五所重点高中12月)已知f(x)=-3x2+a(6-a)x+b.
(1)解关于a的不等式f(1)>0;
(2)当不等式f(x)>0的解集为(-1,3)时,求实数a、b的值.
解:(1)由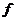 (1)>0得-3+a(6-a)+b>0
(1)>0得-3+a(6-a)+b>0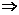 a2-6a+3-b<0,∴(a-3)2<6+b.
a2-6a+3-b<0,∴(a-3)2<6+b.
当b≤-6时,不等式的解集为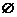 ;
;
当b>-6时,不等式的解集为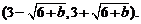 (6分)
(6分)
(2)由f(x)>0得3x2-a(6-a)x-b<0,因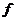 (x)>0的解集为(-1,3),即不等式3x2-a(6-a)x-b<0的解集为(-1,3),故x=-1、x=3是方程3x2-a(6-a)x-b=0的两实根,由韦达定理,得
(x)>0的解集为(-1,3),即不等式3x2-a(6-a)x-b<0的解集为(-1,3),故x=-1、x=3是方程3x2-a(6-a)x-b=0的两实根,由韦达定理,得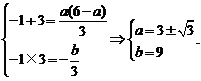 (12分)
(12分)
湖北省2009届高三数学月考模拟分类汇编――平面向量
一、选择题
1、(2009湖北八校第一次月考)若四边形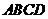 满足:
满足: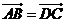 ,且
,且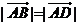 ,则四边形ABCD的形状是( )
,则四边形ABCD的形状是( )
A.矩形 B.正方形 C. 等腰梯形 D.菱形
D
2、(2009黄冈五所重点高中12月)已知O、A、B、C是不共线的四点,若存在一组正实数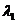 ,
,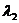 ,
,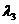 ,使
,使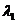
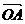 +
+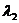
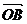 +
+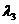
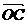 =
= 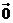 ,则三个角∠AOB,∠BOC,∠COA
,则三个角∠AOB,∠BOC,∠COA
A.都是锐角 B.至多有两个钝角 C.恰有两个钝角 D.至少有两个钝角。
D
3、(2009荆州中学期末)已知向量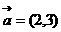 ,
,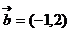 ,若
,若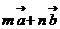 与
与 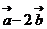 共线,则
共线,则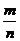 等于( )
等于( )
A.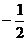 ; B.
; B.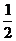 ; C.
; C.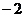 ; D.
; D.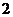 ;
;
A
4、(2009武昌区1月调考)已知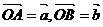 ,www.1010jiajiao.comC为线段AB上距A较近的一个三等分点,D为线段CB上距C 较近的一个三等分点,则用
,www.1010jiajiao.comC为线段AB上距A较近的一个三等分点,D为线段CB上距C 较近的一个三等分点,则用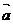 、
、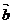 表示
表示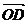 的表达式为(
)
的表达式为(
)
A.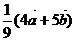 B
B
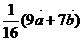 C.
C.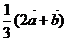 D.
D.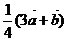
A
5、(2009宜昌一中12月月考)若向量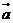 =
=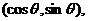
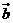 =(1,-1),则|2
=(1,-1),则|2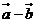 |的取值范围是( )
|的取值范围是( )
(A)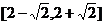 (B)
(B)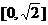 (C)
(C)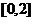 (D)[1,3]
(D)[1,3]
A
二、填空题
1、(2009黄冈五所重点高中12月)如图,半圆的直径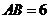 ,
, 为圆心,
为圆心, 为半圆
为半圆
 上不同于
上不同于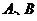 的任意一点,若
的任意一点,若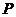 为半径
为半径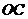 上的动
上的动
点,则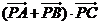 的最小值是__________.
的最小值是__________.
-18
2、(2009武汉市教科院第一次调考)(文科)已知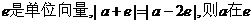 方向上的投影为 。
方向上的投影为 。
(理科)平面上的向量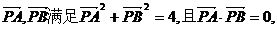 若向量
若向量
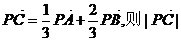 的最大值为 。
的最大值为 。
(文)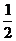 (理)
(理)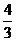
3、(2009咸宁市期末)给出下列命题
① 非零向量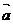 、
、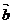 满足|
满足|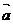 |=|
|=|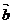 |=|
|=|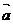 -
-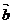 |,则
|,则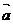 与
与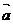 +
+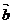 的夹角为30°;
的夹角为30°;
② 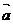 ?
?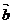 >0是
>0是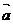 、
、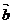 的夹角为锐角的充要条件;
的夹角为锐角的充要条件;
③ 将函数y=|x-1|的图象按向量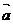 =(-1,0)平移,得到的图像对应的函数为y=|x|;
=(-1,0)平移,得到的图像对应的函数为y=|x|;
④若(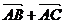 )?(
)?(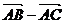 )=0,则△ABC为等腰三角形
)=0,则△ABC为等腰三角形
以上命题正确的是 。(注:把你认为正确的命题的序号都填上)
①③④
三、解答题
1、(2009湖北八校第一次月考)将圆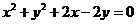 按向量
按向量
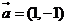 平移得到圆
平移得到圆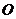 .直线
.直线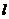 与圆
与圆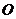 相交于
相交于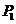 、
、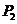 两点,若在圆O上存在点
两点,若在圆O上存在点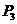 ,使
,使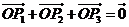 ,且
,且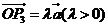 ,求直线
,求直线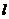 的方程.
的方程.
解:由题意可知圆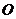 的方程为
的方程为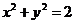 ,于是
,于是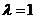 .
.
设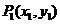 ,
,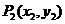 ,则由
,则由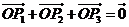 得,
得,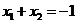 ,
,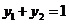 .
.
所以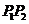 的中点坐标为
的中点坐标为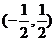 .
.
又由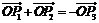 ,且
,且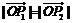 ,可知直线
,可知直线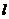 与直线
与直线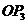 垂直,即直线
垂直,即直线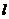 的斜率为
的斜率为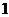 .
.
故直线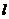 的方程为
的方程为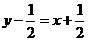 ,即
,即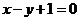 .
.
2、(2009荆州中学期末)设向量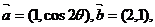
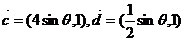 ,其中
,其中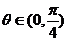 .
.
(1)求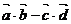 的取值范围;
的取值范围;
(2)若函数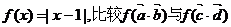 的大小.
的大小.
解:(1)∵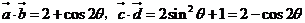 ,
,
∴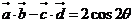 ,
,
∵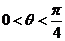 ,∴
,∴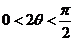 ,∴
,∴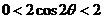 ,
,
∴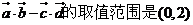 。………………………………….6分
。………………………………….6分
(2)∵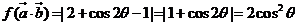 ,
,
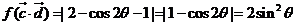 ,
,
∴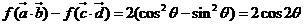 ,
,
∵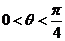 ,∴
,∴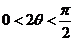 ,∴
,∴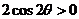 ,∴
,∴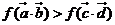 …….12分
…….12分
3、(2009武汉市教科院第一次调考)设函数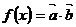 ,其中向量
,其中向量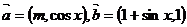 ,
, ,且
,且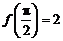 .
.
(Ⅰ)求实数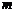 的值;
的值;
(Ⅱ)求函数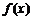 的最小值。
的最小值。
解:(Ⅰ)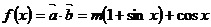 . ……………………………………2分
. ……………………………………2分
由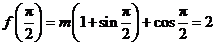 ,得
,得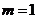 .
………………………………5分
.
………………………………5分
(Ⅱ)由(Ⅰ)得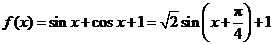 . ………………8分
. ………………8分
 当
当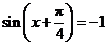 时,
时,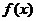 的最小值为
的最小值为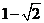 .
……………………………12分
.
……………………………12分
 .w.w.k.s.5.u.c.o.m
.w.w.k.s.5.u.c.o.m
湖北省2009届高三数学月考模拟分类汇编――三角函数
一、选择题
1、(2009湖北八校第一次月考)若函数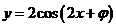 是奇函数,且在
是奇函数,且在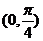 上是增函数,则实数
上是增函数,则实数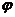 可能是( )
可能是( )
A. B.
B.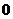 C.
C.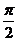 D.
D.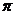
A
2、(2009蕲春一中第四次阶段考)函数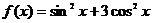 的最小正周期是
的最小正周期是
A、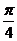 B、
B、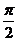 C、
C、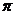 D、
D、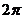
C
3、(2009黄冈市期末)把函数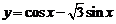 的图象沿向量a=(-m,m)(m>0)的方向平移后,所得的图象关于y轴对称,则m的最小值是( )
的图象沿向量a=(-m,m)(m>0)的方向平移后,所得的图象关于y轴对称,则m的最小值是( )

C
4、(2009黄冈五所重点高中12月)在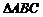 中,角
中,角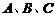 的对边分别是
的对边分别是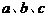 ,且
,且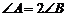 ,则
,则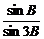 等于
等于
A.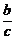 B.
B.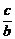 C.
C.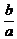 D.
D.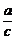
A
5、(2009黄冈五所重点高中12月)设函数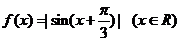 ,则
,则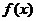
A.在区间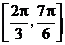 上是增函数 B.在区间
上是增函数 B.在区间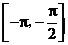 上是减函数
上是减函数
C.在区间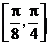 上是增函数 D.在区间
上是增函数 D.在区间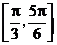 上是减函数
上是减函数
A
6、(2009荆州中学期末)若函数f(x)=asinx-bcosx在x=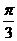 处有最小值-2,则常数a、b的值是( )
处有最小值-2,则常数a、b的值是( )
A.a=-1,b= B.a=1,b=- C.a=,b=-1 D.a=-,b=1 5.
D
7、(2009武汉市教科院第一次调考)
已知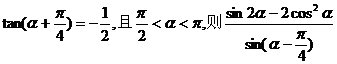 等于 ( )
等于 ( )
A.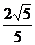 B.
B.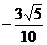 C.
C.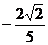 D.
D.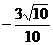
C
8、(2009武昌区1月调考)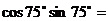 ( )
( )
A.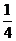 B.
B.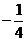 C.
C.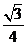 D.
D.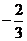
A
9、(2009宜昌一中12月月考)在锐角三角形ABC中设x = (1+sinA) (1+sinB) , y = (1+cosA) (1+cosB) ,则x 、y大小关系为( )
A.x≤y B.x < y C.x≥y D.x > y
D
二、填空题
1、(2009黄冈市期末)△ABC中,边AB为最大边,且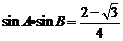 ,则cosA?cos
B的最大值是______.
,则cosA?cos
B的最大值是______.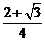
2、(2009蕲春一中第四次阶段考)若tan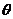 =2,则2sin2
=2,则2sin2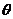 -3
-3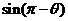
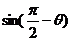 =
=
-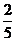
三、解答题
1、(2009湖北八校第一次月考)已知函数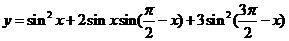 .
.
⑴若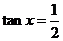 ,求
,求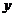 的值;
的值;
⑵若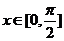 ,求
,求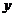 的值域.
的值域.
解: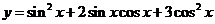
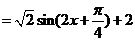
⑴ 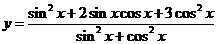
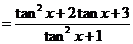
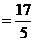 .
.
⑵ 函数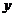
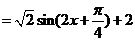 在
在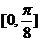 上单调递增,在
上单调递增,在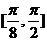 上单调递减.
上单调递减.
所以,当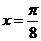 时,
时,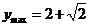 ;当
;当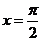 时,
时,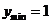 .
.
故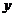 的值域为
的值域为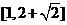 .
.
2、(2009黄冈市期末)已知,θ∈[0,2π),sinθ、cosθ分别是方程x2-kx+k+1=0的两实根,求θ的值.
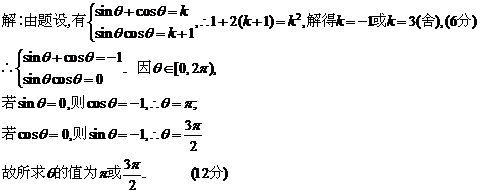
3、(2009黄冈五所重点高中12月)已知在锐角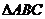 中,角
中,角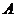 、
、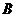 、
、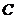 的对边分别为
的对边分别为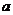 、
、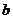 、
、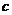 ,且
,且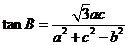 ,
,
(I)求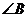 ;
;
(II)求函数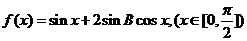 的最小值及单调递减区间.
的最小值及单调递减区间.
解(1)由题意得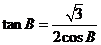 , ………2分 ; 从而
, ………2分 ; 从而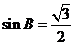 , ………4分
, ………4分
又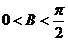 ,所以
,所以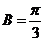 ………………………………………6分
………………………………………6分
(2)由(1)得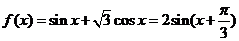 ………………………8分
………………………8分
因为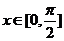 ,所以
,所以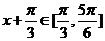 ,所以当
,所以当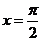 时,
时,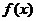 取得最小值为1…10分
取得最小值为1…10分
且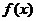 的单调递减区间为
的单调递减区间为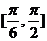 ………………………………12分
………………………………12分
4、(2009武汉市教科院第一次调考)已知向量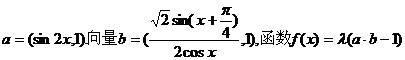
(1)(文科)若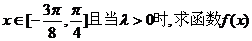 的单调递减区间;
的单调递减区间;
(2)(理科)若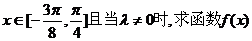 的单调递减区间;
的单调递减区间;
(3)当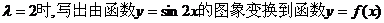 的图象的变换过程。
的图象的变换过程。
解:(1)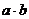
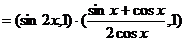
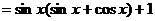

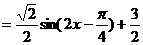
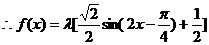 …………(4分)
…………(4分)
(1)(文科)在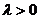 时,
时,
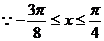
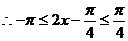
在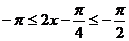 时,
时,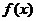 为减函数
为减函数
从而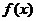 的单调递减区间为
的单调递减区间为 ;…………(文8分)
;…………(文8分)
(2)(理科)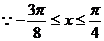
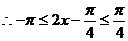
当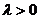 时,由
时,由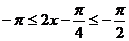 得单调递减区间为
得单调递减区间为
同理,当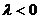 时,函数的单调递减区间为
时,函数的单调递减区间为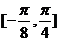 …………(理8分)
…………(理8分)
(3)当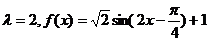 ,变换过程如下:
,变换过程如下:
1°将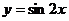 的图象向右平移
的图象向右平移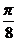 个单位可得函数
个单位可得函数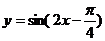 的图象。
的图象。
2°将所得函数图象上每个点的纵坐标扩大为原来的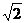 倍,而横坐标保持不变,可得函数
倍,而横坐标保持不变,可得函数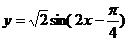 的图象。
的图象。
3°再将所得图象向上平移一个单位,可得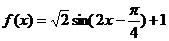 的图象……(12分)
的图象……(12分)
5、(2009宜昌一中12月月考)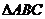 中,角
中,角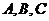 所对的边分别为
所对的边分别为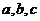 且
且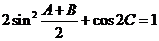
(1)求角的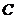 大小;
大小;
(2)若向量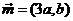 ,向量
,向量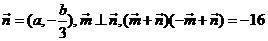 ,求
,求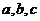 的值。
的值。
解:(1)∵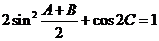
∴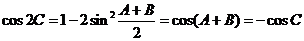 ,…………………(2分)
,…………………(2分)
∴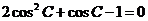 ,∴
,∴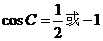
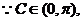 ∴
∴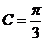 …(4分)
…(4分)
(2)∵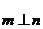 ∴
∴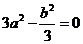 ,即
,即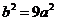
又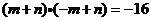 ,∴
,∴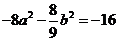 ,即
,即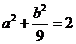 ②………6分
②………6分
由①②可得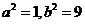 ,∴
,∴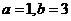 ……………………………(8分)
……………………………(8分)
又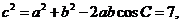 ∴
∴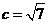 ,
,
 w.w.w
w.w.w
湖北省2009届高三数学月考模拟分类汇编―应用题
一、选择、填空题
1、(2009蕲春一中第四次阶段考)某实验室需购某种化工原料106千克,现在市场上该原料有两种包装,一种是每袋35千克,价格为140元;另一种是每袋24千克,价格为120元. 在满足需要的条件下,最少要花费
元.
500
2、(2009随州曾都一中第一次月考)某商场在中秋节促销期间规定,商场内所有商品按标价的80%出售;同时,当顾客在该商场内消费满一定金额后,按如下方案获得相应金额的奖券:
消费金额(元)的范围
[200,400)
[400,500)
[500,700)
[700,900 )
…
获得奖券的金额(元)
30
60
100
130
…
根据上述促销方法,顾客在该商场购物可以获得双重优惠,例如,购买标价为400元的商品,则消费金额为320元,获得的优惠额为:400×0.2+30=110(元).若顾客购买一件标价为1000元的商品,则所能得到的优惠额为
A.130元 B.330元 C.360元 D.800元
B
二、解答题
1、(2009湖北八校第一次月考)某地正处于地震带上,预计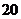 年后该地将发生地震.当地决定重新选址建设新城区,同时对旧城区进行拆除.已知旧城区的住房总面积为
年后该地将发生地震.当地决定重新选址建设新城区,同时对旧城区进行拆除.已知旧城区的住房总面积为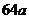
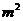 ,每年拆除的数量相同;新城区计划用十年建成,第一年建设住房面积
,每年拆除的数量相同;新城区计划用十年建成,第一年建设住房面积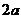
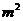 ,开始几年每年以
,开始几年每年以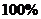 的增长率建设新住房,然后从第五年开始,每年都比上一年减少
的增长率建设新住房,然后从第五年开始,每年都比上一年减少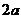
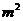

⑴ 若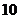 年后该地新、旧城区的住房总面积正好比目前翻一番,则每年旧城区拆除的住房面积是多少
年后该地新、旧城区的住房总面积正好比目前翻一番,则每年旧城区拆除的住房面积是多少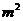 ?
?
⑵ 设第
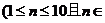 N)年新城区的住房总面积为
N)年新城区的住房总面积为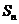
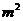 ,求
,求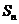 .
.
解:⑴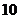 年后新城区的住房总面积为
年后新城区的住房总面积为
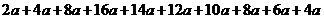
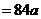 .
.
设每年旧城区拆除的数量是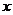 ,则
,则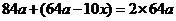 ,
,
解得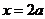 ,即每年旧城区拆除的住房面积是
,即每年旧城区拆除的住房面积是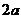
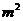 .
.
⑵设第 年新城区的住房建设面积为
年新城区的住房建设面积为 ,则
,则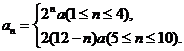 所以
所以
当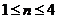 时,
时,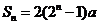 ;
;
当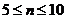 时,
时,
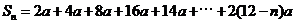
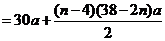
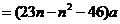 .
.
故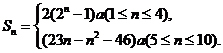
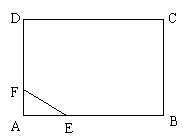 2、(2009黄冈五所重点高中12月)“
2、(2009黄冈五所重点高中12月)“ ”汶川大地震是华人心中永远的痛!
”汶川大地震是华人心中永远的痛!
在灾后重建中拟在矩形区域ABCD内建
一矩形的汶川人民纪念广场(如图),另
外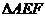 内部有一废墟作为文物保护区
内部有一废墟作为文物保护区
不能占用。经测量AB=100m,BC=80m,
AE=30m,AF=20m,如何设计才能使广场
面积最大?
解:建立如图所示的直角坐标系,则E(30,0),F(0,20)。
∴线段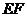 的方程是
的方程是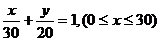 ………3分
………3分
设矩形PQCR的面积为s,则s=|PQ|?|PR|=(100-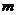 )(80-
)(80- ).…………6分
).…………6分
又∵ 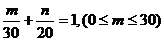 ,∴
,∴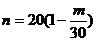 ,
,
∴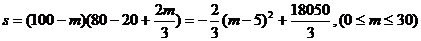 。……10分
。……10分
∴当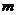 =5m时,s有最大值,此时
=5m时,s有最大值,此时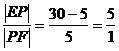 .
.
故当矩形广场的两边在BC、CD上,一个顶点在线段EF上,
且这个顶点分EF成5:1时,广场的面积最大。 …………12分
3、(2009随州曾都一中第一次月考)某市旅游部门开发一种旅游纪念品,每件产品的成本是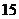 元,销售价是
元,销售价是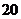 元,月平均销售
元,月平均销售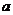 件.通过改进工艺,产品的成本不变,质量和技术含金量提高,市场分析的结果表明,如果产品的销售价提高的百分率为
件.通过改进工艺,产品的成本不变,质量和技术含金量提高,市场分析的结果表明,如果产品的销售价提高的百分率为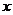
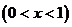 ,那么月平均销售量减少的百分率为
,那么月平均销售量减少的百分率为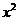 .记改进工艺后,旅游部门销售该纪念品的月平均利润是
.记改进工艺后,旅游部门销售该纪念品的月平均利润是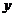 (元).
(元).
(1)写出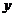 与
与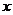 的函数关系式;
的函数关系式;
(2)改进工艺后,确定该纪念品的销售价,使旅游部门销售该纪念品的月平均利润最大.
解(1)改进工艺后,每件产品的销售价为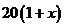 ,月平均销售量为
,月平均销售量为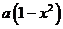 件,则月平均利润
件,则月平均利润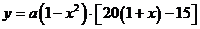 (元),∴
(元),∴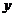 与
与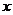 的函数关系式为
的函数关系式为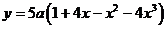
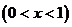 6分
6分
(2)由 得
得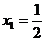 ,
,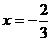 (舍)
(舍)
当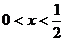 时
时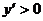 ;
;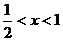 时
时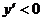 ,∴函数
,∴函数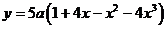
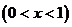 在
在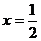 取得最大值.故改进工艺后,产品的销售价为
取得最大值.故改进工艺后,产品的销售价为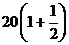
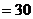 元时,旅游部门销售该纪念品的月平均利润最大.
12分
元时,旅游部门销售该纪念品的月平均利润最大.
12分
4、、(2009浠水一中模拟)统计表明,某种型号的汽车在匀速行驶中每小时的耗油量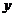 (升)关于行驶速度
(升)关于行驶速度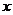 (千米/小时)的函数解析式可以表示为:
(千米/小时)的函数解析式可以表示为:
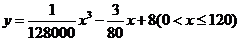 .已知甲、乙两地相距100千米
.已知甲、乙两地相距100千米
(Ⅰ)当汽车以40千米/小时的速度匀速行驶时,从甲地到乙地要耗油多少升?
(II)当汽车以多大的速度匀速行驶时,从甲地到乙地耗油最少?最少为多少升?
解:I)当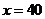 时,汽车从甲地到乙地行驶了
时,汽车从甲地到乙地行驶了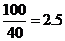 小时,
小时,
要耗没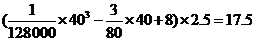 (升)。
(升)。
答:当汽车以40千米/小时的速度匀速行驶时,从甲地到乙地耗油17.5升。
(II)当速度为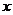 千米/小时时,汽车从甲地到乙地行驶了
千米/小时时,汽车从甲地到乙地行驶了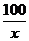 小时,设耗油量为
小时,设耗油量为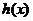 升,
升,
依题意得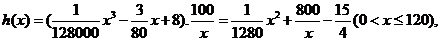
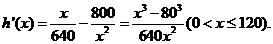
令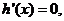 得
得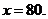 当
当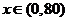 时,
时,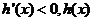 是减函数;
是减函数;
当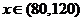 时,
时,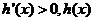 是增函数。
是增函数。 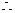 当
当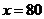 时,
时,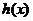 取到极小值
取到极小值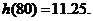 因为
因为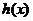 在
在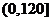 上只有一个极值,所以它是最小值。
上只有一个极值,所以它是最小值。
答汽车以80千米/小时的速度匀速行驶时,从甲地到乙地耗油最少,最少为11.25升。
5、(2009湖北补习学校联考)武汉东湖风景区有50辆自行车供游客租赁使用,管理这些自行车
的费用是每日115元。根据经验,若每辆自行车的日租金不超过6元,则自行车可以全部
租出;若超出6元,则每超过1元,租不出的自行车就增加3辆。为了便于结算,每辆自
行车的日租金x(元)只取整数,并且要求出租自行车一日的总收入必须高于这一日的管
理费用,用y(元)表示出租自行车的日净收入(即一日中出租自行车的总收入减去管理
费用后的所得)。
(1)求函数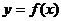 的解析式及其定义域;
的解析式及其定义域;
(2)试问当每辆自行车的日租金定为多少元时,才能使一日的净收入最多?
解:(1)当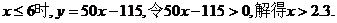
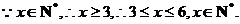 ………………2分
………………2分
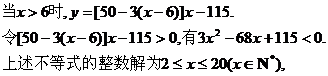
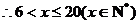 ,..............................................5分
,..............................................5分
故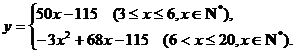 ................6分
................6分
定义域为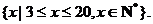 .................................7分
.................................7分
(2)对于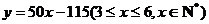 ,
,
显然当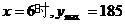 (元), ..................................9分
(元), ..................................9分
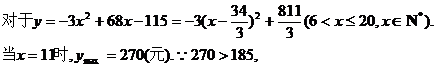
∴当每辆自行车的日租金定在11元时,才能使一日的净收入最多。..........12分
 w.w.w.k.s.5.u.c.o.m
w.w.w.k.s.5.u.c.o.m
湖北省2009届高三数学月考模拟分类汇编――数列
一、选择题
1、(2009湖北八校第一次月考)已知数列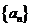 的前
的前 项的和
项的和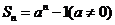 ,则
,则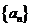 ( )
( )
A.一定是等差数列 B.一定是等比数列
C.或者是等差数列,或者是等比数列 D.既不可能是等差数列也不可能是等比数列
C
2、(2009湖北八校第一次月考) 数列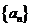 中,
中,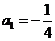 ,
,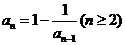 ,则
,则 ( )
( )
A. B.
B.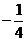 C.
C.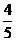 D.
D.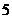
B
3、(2009黄冈市期末)在等比数列{an}中,若a5+a6=a(a≠0),a15+a16=b,则a25+a26的值是( )

C
4、(2009黄冈五所重点高中12月)n个连续自然数按规律排成下表:根据规律,
从2006到2008,箭头的方向依次为
A.↓→ B.↑→
C.→↑ D.→↓
 B
B
5、(2009荆州中学期末)如果数列{an}满足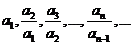 是首项为1,公比为2的等比数列,则a100等于
是首项为1,公比为2的等比数列,则a100等于
A.2100 B.299 C.25050 D.24950
D
6、(2009武汉市教科院第一次调考)(文科)在等比数列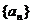 中,若
中,若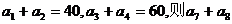 = ( )
= ( )
A.100 B.80 C.95 D.135
D
7、(2009武汉市教科院第一次调考)(理科)已知Sn表示等差数列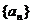 的前n项和,且
的前n项和,且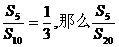 = ( )
= ( )
A.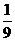 B
B
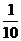 C.
C.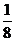 D.
D.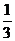
B
8、(2009武昌区1月调考)已知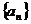 为等差数列,
为等差数列,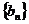 为等比数列,其公比
为等比数列,其公比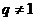 ,且
,且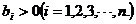 ,若
,若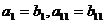 ,则
( )
,则
( )
A.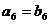 B.
B.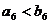 C.
C. 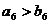 D.
D.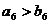 或
或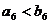
C
9、(2009咸宁市期末)若等差数列{an}的前5项和S5=25,且a2=3,则a4= ( )
A.12 B.7
C.9 D.15
B
10、(2009宜昌一中12月月考)已知数列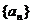 的通项公式为
的通项公式为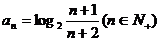 ,设其前n项和为Sn,则使Sn<-5成立的自然数n 有( )
,设其前n项和为Sn,则使Sn<-5成立的自然数n 有( )
A.最小值63 B.最大值63 C.最小值31 D.最大值31
A
二、解答题
1、(2009黄冈市期末)在等比数列{an}(n∈N*)中,已知a1>1,q>0.设bn=log2an,且b1+b3+b5=6,b1b3b5=0.
(1)求数列{an}、{bn}的通项公式an、bn;
(2)若数列{bn}的前n项和为Sn,试比较Sn与an的大小.
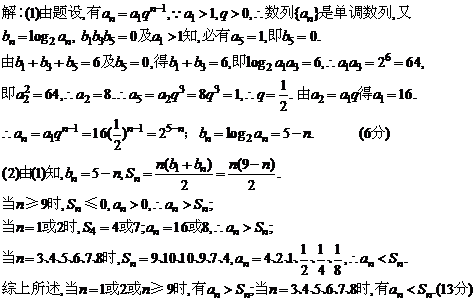
2、(2009黄冈五所重点高中12月)已知二次函数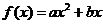 满足条件:①
满足条件:①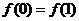 ; ②
; ②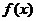 的最小值为
的最小值为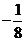 .
.
(Ⅰ)求函数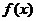 的解析式;
的解析式;
(Ⅱ)设数列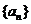 的前
的前 项积为
项积为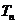 , 且
, 且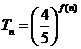 , 求数列
, 求数列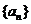 的通项公式;
的通项公式;
(Ⅲ)
在(Ⅱ)的条件下, 若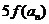 是
是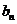 与
与 的等差中项, 试问数列
的等差中项, 试问数列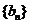 中第几项的
中第几项的
值最小? 求出这个最小值.
解: (1) 由题知: 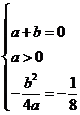 , 解得
, 解得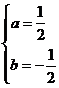 , 故
, 故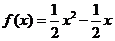 . ………2分
. ………2分
(2) 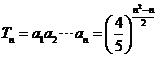 ,
,
 ,
,
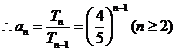 ,
,
又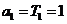 满足上式. 所以
满足上式. 所以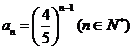 ……………7分
……………7分
(3) 若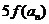 是
是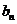 与
与 的等差中项, 则
的等差中项, 则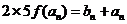 ,
,
从而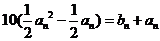 , 得
, 得 .
.
因为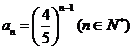 是
是 的减函数, 所以
的减函数, 所以
当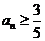 , 即
, 即 时,
时, 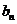 随
随 的增大而减小, 此时最小值为
的增大而减小, 此时最小值为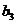 ;
;
当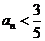 , 即
, 即 时,
时, 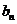 随
随 的增大而增大, 此时最小值为
的增大而增大, 此时最小值为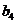 .
.
又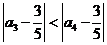 , 所以
, 所以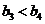 ,
,
即数列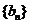 中
中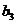 最小, 且
最小, 且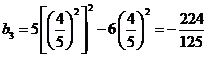 . …………12分
. …………12分
3、(2009荆州中学期末)
6、(2009随州曾都一中第一次月考)
7、(2009武汉市教科院第一次调考)
8、(2009武昌区1月调考)
9、(2009浠水一中模拟)
10、(2009咸宁市期末)已知数列{an}的前n项和为Sn,且an是Sn与2的等差中项,数列{bn}中,b1=1,
点P(bn,bn+1)在直线x-y+2=0上。
(1)求a1和a2的值;
(2)求数列{an},{bn}的通项an和bn;
(3)设cn=an?bn,求数列{cn}的前n项和Tn。
解:
(1)∵an是Sn与2的等差中项
∴Sn=2an-2 ∴a1=S1=2a1-2,解得a1=2
a1+a2=S2=2a2-2,解得a2=4 ???3分
(2)∵Sn=2an-2,Sn-1=2an-1-2,
又Sn―Sn-1=an,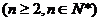
∴an=2an-2an-1,
∵an≠0,
∴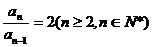 ,即数列{an}是等比树立∵a1=2,∴an=2n
,即数列{an}是等比树立∵a1=2,∴an=2n
∵点P(bn,bn+1)在直线x-y+2=0上,∴bn-bn+1+2=0,
∴bn+1-bn=2,即数列{bn}是等差数列,又b1=1,∴bn=2n-1, ???8分
(3)∵cn=(2n-1)2n
∴Tn=a1b1+ a2b2+????anbn=1×2+3×22+5×23+????+(2n-1)2n,
∴2Tn=1×22+3×23+????+(2n-3)2n+(2n-1)2n+1
因此:-Tn=1×2+(2×22+2×23+???+2×2n)-(2n-1)2n+1,
即:-Tn=1×2+(23+24+????+2n+1)-(2n-1)2n+1,
∴Tn=(2n-3)2n+1+6 ??14分
11、(2009宜昌一中12月月考)设等差数列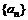 的前n项和为Sn,公差d >0,若
的前n项和为Sn,公差d >0,若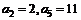 。
。
(1)求数列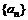 的通项公式;
的通项公式;
(2) 设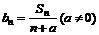 ,若
,若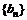 是等差数列且
是等差数列且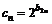 ,求实数a与
,求实数a与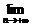
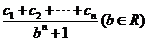 的值。
的值。
解:(1)设等差数列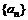 的通项为
的通项为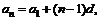
由题得: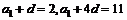 ,
2分
,
2分
解得: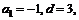
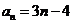 4分
4分
(2)由(1)得: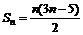 6分
6分
∴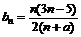
则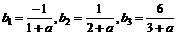 ,
,
∵{bn}是等差数列,则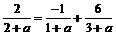
∴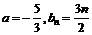 8分
8分
又∵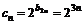
∴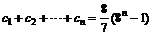 10分
10分
故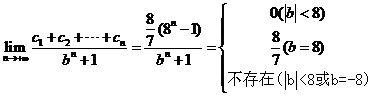 12分
12分
 w.w.w.k.s.5.u.c.o.m
w.w.w.k.s.5.u.c.o.m
湖北省2009届高三数学月考模拟分类汇编――立体几何
一、选择题
1、(2009蕲春一中第四次阶段考)已知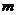 、
、 是直线,
是直线,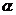 、
、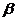 、
、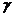 是平面,给出下列五个命题:
是平面,给出下列五个命题:
①若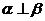 ,
,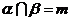 ,
,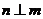 则
则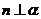 或
或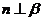
②若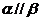 ,
,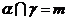 ,
,  则
则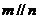
③若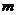 不垂直于
不垂直于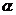 ,则
,则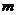 不可能垂直于
不可能垂直于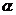 内的无数条直线
内的无数条直线
④若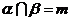 ,
, 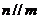 ,且
,且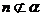 ,
,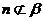 则
则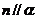 且
且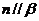
⑤若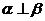 ,
,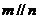 ,
,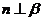 则
则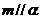 或
或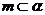 其中真命题的个数是
( )
其中真命题的个数是
( )
A.1 B.2 C.3 D.4
C
2、、(2009武汉市教科院第一次调考)已知直线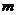 、
、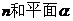 ,下列命题中的真命题是 ( )
,下列命题中的真命题是 ( )
A.如果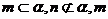 、
、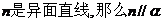 ;
;
B.如果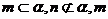 、
、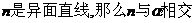 ;
;
C.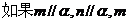 、
、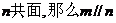 ;
;
D.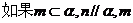 、
、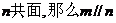 ;
;
D
3 (2009武昌区1月调考)下列命题正确的是(
)
(2009武昌区1月调考)下列命题正确的是(
)
A.垂直于同一直线的两条直线平行
B.若一条直线垂直于两条平行线中的一条,则它垂直于另一条
C.若一条直线与两条平行线中的一条相交,则它与另一条相交
D.一条直线至多与两条异面直线中的一条相交
B
4、(2009咸宁市期末)平面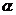 、
、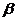 、
、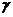 两两互相垂直,点A∈
两两互相垂直,点A∈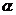 ,点A到
,点A到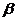 、
、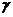 的距离都是3,P是
的距离都是3,P是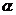 上的
上的
动点,P到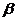 的距离是到点A距离的2倍,则点P的轨迹上的点到
的距离是到点A距离的2倍,则点P的轨迹上的点到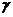 的距离的最小值
的距离的最小值
( )
A.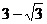 B.
B.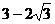
C.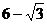 D.
D.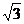
5、(2009咸宁市期末)如图在棱长为a的正方体ABCD―A1B1C1D1中,
P为A1D1的中点,Q为A1B1上任意一点,E、F
为CD上任意两点,且EF的长为定值b,则下列
四个值中不为定值的是 ( )
A.点到平面的距离
B.二面角的大小
C.直线与平面所成的角
D.三棱锥的体积
A
二、解答题
1、(2009蕲春一中第四次阶段考)如图,在底面是矩形的四棱锥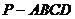 中,
中,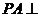 面ABCD,PA=AB=1,BC=2
面ABCD,PA=AB=1,BC=2
解、以A为原点,AB所在直线为x轴,AD所在直线为y轴,AP所在直线为z轴建系,则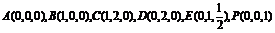
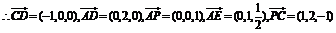
(Ⅰ)易证得CD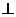 AD,CD
AD,CD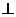 AP 则CD
AP 则CD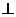 面PAD
面PAD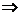 平面PDC
平面PDC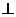 平面PAD ……………4分
平面PAD ……………4分
(Ⅱ)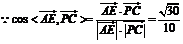 所以 所求角的余弦值为
所以 所求角的余弦值为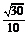 ………8分
………8分
(Ⅲ)假设存在,设BG=x,则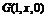 ,作DQ
,作DQ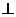 AG,则DQ
AG,则DQ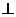 平面PAG,即DG=1,
平面PAG,即DG=1,
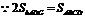 ,
,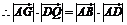
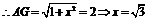 故存在点G,当
故存在点G,当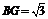 时,D到平面PAG的距离为1。
12分
时,D到平面PAG的距离为1。
12分
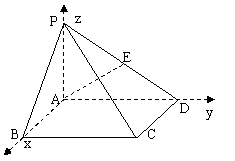
2、(2009武汉市教科院第一次调考)如图,在直三棱柱ABC―A1B1C1中,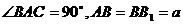 ,直线B1C与
,直线B1C与
平面ABC成30°角。
(1)求证:平面B1AC⊥平面ABB1A1;
(2)(文科)求二面角B―B1C―A的正切值;
(3)(理科)求直线A1C与平面B1AC所成的角的正弦值。
|