
题目列表(包括答案和解析)
4.一次函数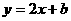 的图象与坐标轴围成的三角形的面积是9,则
的图象与坐标轴围成的三角形的面积是9,则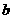 =____.
=____.
3.若一次函数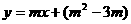 图象过原点,则
图象过原点,则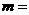 ____.若图象与
____.若图象与 轴交于点(0,4),则
轴交于点(0,4),则 =____.
=____.
2.函数 的图象经过点(-2,6),则它的图象经过第____象限,它的图象 象与
的图象经过点(-2,6),则它的图象经过第____象限,它的图象 象与 交于____,与
交于____,与 轴的交点坐标是____,它的图象与坐标轴围成的三角形面积是____.
轴的交点坐标是____,它的图象与坐标轴围成的三角形面积是____.
(1)填空题:
1.函数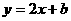 的图象经过点(1,-3),则b=____,它的图象经过第____象限,
的图象经过点(1,-3),则b=____,它的图象经过第____象限, 随
随 的增大而____.
的增大而____.
例1:已知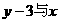 成正比例,且
成正比例,且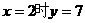
(1)求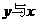 间的函数解析式.
间的函数解析式.
(2)求当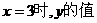 .
.
(3)求当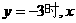 的值.
的值.
解:(1)∵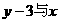 成正比例
成正比例
∴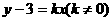
把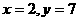 代入上式得k=2
代入上式得k=2
∴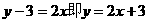
注意: [1]因为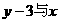 成正比例,把
成正比例,把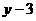 看成一个变量
看成一个变量
2]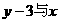 成正比例,设
成正比例,设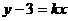 .
.
(2)当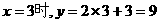 .
.
(3)当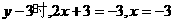 .
.
例2:已知一次函数的图象经过(1,1)和(-1,-5)
求(1)此函数解析式.
(2)求此函数与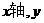 轴的交点坐标及它的图象与两坐标轴围成的三角形面积.
轴的交点坐标及它的图象与两坐标轴围成的三角形面积.
(3)设另一条相干直线与此一次函数图象交于(-1,m)点,且与 轴交点的纵坐标是4,求这条直线的解析式.
轴交点的纵坐标是4,求这条直线的解析式.
解:(1)设一次函数的解析式是
 将
将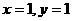 和
和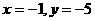 代入得
代入得 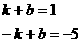
解得 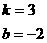
∴此一次函数解析式为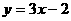
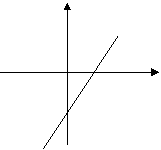 (2)对
(2)对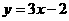 ,令
,令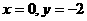 则图象与
则图象与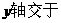 A(0,-2)令
A(0,-2)令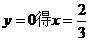 ,则此函数与
,则此函数与 轴交于B(
轴交于B(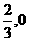 ).
y
).
y
图象与两坐标轴围成的三角形面积
O B(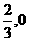 ) x
) x
是SΔAOB,其底长|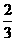 |个单位,高|-2|=2
A(0,-2)
|个单位,高|-2|=2
A(0,-2)
个单位.
∴SΔAOB=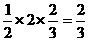
(3)由于(-1,m)即在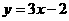 图象上,又在所求的另一条直线上,所以(-1,m)满足y=3x-2,将x=-1,y=m,代入y=3x-2得m=-5,所以两直线交于(-1,-5),说明第二条直线也经过(-1,-5)且还经过(0,4).
图象上,又在所求的另一条直线上,所以(-1,m)满足y=3x-2,将x=-1,y=m,代入y=3x-2得m=-5,所以两直线交于(-1,-5),说明第二条直线也经过(-1,-5)且还经过(0,4).
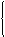 设另一条直线为y1=k1x+b,将x=-1,y=-5.x=0,y=4代入得
设另一条直线为y1=k1x+b,将x=-1,y=-5.x=0,y=4代入得 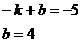

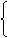 ∴
∴ 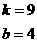
∴第二条直线的解析式是y=9x+4.
例3:一次函数y=2x+3的图象与y轴交于A,另一个次函数图象与y轴交于B,两条直线交于C,C点的纵坐标是1,且SΔABC=16,求另一条直线的解析式.
解:∵y=2x-3与y轴交于A(0,-3)
设另一条直线的解析式是y=kx+b,则它与y轴交于B(0,b)
∵两直线交于C,C的纵坐标是1,设C(x,1) y y=2x-3
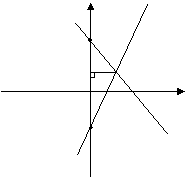 ∴C在y=2x-3上
∴C在y=2x-3上
∴将y=1代入y=2x-3中得x=2 B(0,b)
∴C的坐标是(2,1)
画草图分析 C(2,1)
则ΔABC的底AB=|b-(-3)|=|b+3| x
高是C点的横坐标|2|=2 A(0,-3)
由题意得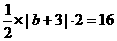 y=kx+b
y=kx+b
|b+3|=16
b+3=16或b=-19则函数解析式是y=kx+13或y=kx-19再将x=2,y=1代入得k=-6或k=10.
∴所求函数解析式为y=-6x+13或y=10x -19
(注意:画草图分析是非常必要的.否则此题的解题思路不会清楚).
6.利用待定系数法确定正比例函数和一次函数的解析式,一般步骤是:
①先设出函数的一般形式,如求正比例函数解析式时,先设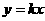 ,求一次函数的解析式时,先设
,求一次函数的解析式时,先设 。
。
②将自变量 的值及与它对应的函数值
的值及与它对应的函数值 的值代入所设的解析式,得到关于待定系数的方程或方程组。
的值代入所设的解析式,得到关于待定系数的方程或方程组。
③解方程或方程组,求出待定系数的值,进而写出函数解析式。
(注意:求正比例函数,只要一对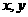 的值就可以,因为它只有一个待定系数;而求一次函数
的值就可以,因为它只有一个待定系数;而求一次函数 则需要两组
则需要两组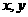 的值。)
的值。)
5.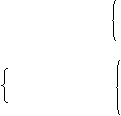 两条直线
两条直线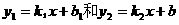 的交点坐标是方程组
的交点坐标是方程组 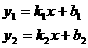 的解.如y=x-2和y=-3x+1的交点坐标就是方程组
的解.如y=x-2和y=-3x+1的交点坐标就是方程组 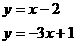 的解
的解 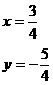 即交点坐标是(
即交点坐标是(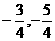 )。
)。
4.如果在 轴上有两个点
轴上有两个点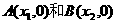 ,则A、B两点的距离是| x2-x1|,如(-1,0)和(3,0)两点的距离就是|3-(-1)|=4,在
,则A、B两点的距离是| x2-x1|,如(-1,0)和(3,0)两点的距离就是|3-(-1)|=4,在 轴上有两点A(0,y1)和B(0,y 2),则A、B两点的距离是|y2-y1|,如(0,2)和(0,-5)的距离是|-5-2|=7。
轴上有两点A(0,y1)和B(0,y 2),则A、B两点的距离是|y2-y1|,如(0,2)和(0,-5)的距离是|-5-2|=7。
3.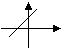
 的图象的性质中
的图象的性质中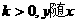 的增大而增大,
的增大而增大,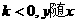 的增大而减少,此性质反映在图象上是
的增大而减少,此性质反映在图象上是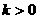 时图象自左而右是“上升”的,如
时图象自左而右是“上升”的,如
反之,图象自左而右是上升的,则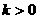 ;
;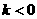 图象自左而右是“下降”的,如
图象自左而右是“下降”的,如
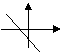
。由于 与
与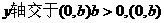 在
在 轴的正半轴上,直线与
轴的正半轴上,直线与
 轴交于正半轴,
轴交于正半轴,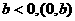 在
在 轴的负半轴,
轴的负半轴, 与
与 轴交于负半轴。
轴交于负半轴。
 y
y
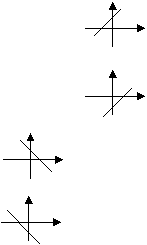
① 的图象在一、二、三象限 0 x
的图象在一、二、三象限 0 x
y
② 的图象在一、三、四象限 0 x
的图象在一、三、四象限 0 x
y
③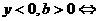 图象在一、二、四象限 0 x
图象在一、二、四象限 0 x
y
④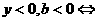 图象在二、三、四象限 0 x
图象在二、三、四象限 0 x
2.课本中,用具体的函数利用描点法得出正比例函数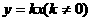 和一次函数
和一次函数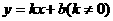 的图象都是一条直线,既然是一条直线,我们只要描出两点即可确定该直线。因为正比例函数是过原点的直线,当然坐标原点是所描的两点中的一个,另外一个是
的图象都是一条直线,既然是一条直线,我们只要描出两点即可确定该直线。因为正比例函数是过原点的直线,当然坐标原点是所描的两点中的一个,另外一个是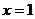 时y=k就是点
时y=k就是点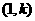 ,所以正比例函数的图像是过(0,0)、(1,k)两点的直线。而一次函数与两条坐标轴各有一个交点(注意:与x轴、y轴交点的坐标是极其重要的),那么“两点确定一条直线”中的两点就可以取这两个交点,由于一次函数与x轴的交点必在x轴上,而在x轴上的点的特点是纵坐标为0,即:在一次函数
,所以正比例函数的图像是过(0,0)、(1,k)两点的直线。而一次函数与两条坐标轴各有一个交点(注意:与x轴、y轴交点的坐标是极其重要的),那么“两点确定一条直线”中的两点就可以取这两个交点,由于一次函数与x轴的交点必在x轴上,而在x轴上的点的特点是纵坐标为0,即:在一次函数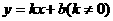 中,当y=0时可得kx+b=0,解此方程得x=-
中,当y=0时可得kx+b=0,解此方程得x=-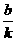 ,从而得出一次函数
,从而得出一次函数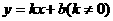 与x轴交于(-
与x轴交于(-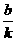 ,0)点;同理,由一次函数
,0)点;同理,由一次函数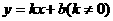 与y轴交点的横坐标为0可以得出:它与y轴的交点为(0,b);因此一次函数
与y轴交点的横坐标为0可以得出:它与y轴的交点为(0,b);因此一次函数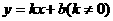 的图象是过它与x轴的交点(-
的图象是过它与x轴的交点(-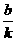 ,0)和它与y轴的交点(0,b)两点的直线。(实践证明,很多同学不会求直线与轴的交点坐标,这是不会解一些一次函数题目的直接原因)。例如描述
,0)和它与y轴的交点(0,b)两点的直线。(实践证明,很多同学不会求直线与轴的交点坐标,这是不会解一些一次函数题目的直接原因)。例如描述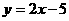 的图象:令
的图象:令 ,令
,令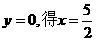 ,所以
,所以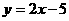 的图像是过
的图像是过 轴上的(0,-5)和x轴上的(
轴上的(0,-5)和x轴上的(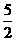 ,0)两点的直线。
,0)两点的直线。
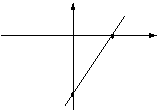
x
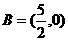
A(0,5)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com