
题目列表(包括答案和解析)
(一)圆的有关性质,本节中最重要的定理有4个.
1.垂径定理:本定理和它的三个推论说明: 在(1)垂直于弦(不是直径的弦);(2)平分弦;(3)平分弦所对的弧;(4)过圆心(是半径或是直径)这四个语句中,满足两个就可得到其它两个的结论.如垂直于弦(不是直径的弦)的直径,平分弦且平分弦所对的两条弧。条件是垂直于弦(不是直径的弦)的直径,结论是平分弦、平分弧。再如弦的垂直平分线,经过圆心且平分弦所对的弧。条件是垂直弦,、分弦,结论是过圆心、平分弦.
应用:在圆中,弦的一半、半径、弦心距组成一个直角三角形,利用勾股定理解直角三角形的知识,可计算弦长、半径、弦心距和弓形的高.
2.圆心角、弧、弦、弦心距四者之间的关系定理:在同圆和等圆中, 圆心角、弧、弦、弦心距这四组量中有一组量相等,则其它各组量均相等.这个定理证弧相等、弦相等、圆心角相等、弦心距相等是经常用的.
3.圆周角定理:此定理在证题中不大用,但它的推论,即弧相等所对的圆周角相等;在同圆或等圆中,圆周角相等,弧相等.直径所对的圆周角是直角,90°的圆周角所对的弦是直径,都是很重要的.条件中若有直径,通常添加辅助线形成直角.
4.圆内接四边形的性质:略.
(二)填空题:
1.若圆的半径是2cm,一条弦长是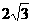 ,则圆心到该弦的距离是______.
,则圆心到该弦的距离是______.
2.在⊙O中,弦AB为24,圆心到弦的距离为5,则⊙O的半径是______cm.
3.若AB是⊙O的直径,弦CD⊥AB于E,AE=9cm,BE=16cm,则CD=______cm.
4. 若⊙O的半径是13cm,弦AB=24cm,弦CD=10cm,AB∥CD,则弦AB与CD之间的距离是______cm.
5. ⊙O的半径是6,弦AB的长是6,则弧AB的中点到AB的中点的距离是______.
6.
 如图:⊙O的直径AB⊥CD于P,
如图:⊙O的直径AB⊥CD于P,
AP=CD=4cm,则OP=______cm.
7. 已知⊙O中,AB是弦,CD是直径,且CD⊥AB于M.⊙O的半径是15cm,OM:OC=3:5,则AB=______.
8.
已知O到直线l的距离OD是 cm,l上一点P,PD=
cm,l上一点P,PD=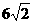 cm.⊙O的直径是20,则P在⊙O______.
cm.⊙O的直径是20,则P在⊙O______.
 (三)证明题:
(三)证明题:
1.如图:AB是⊙O的直径,CD是弦
CE⊥CD于C,DF⊥CD于D
求证:AE=BF
2.⊙O和⊙O1相交于A,B.过A做CAD∥OO1
 求证:CD=2OO1
求证:CD=2OO1
(一)判断题
1.直径是弦.( )
2.半圆是弧,但弧不一定是半圆. ( )
3.到点O的距离等于2cm的点的集合是以O为圆心,2cm为半径的圆. ( )
4.过三点可以做且只可以做一个圆. ( )
5.三角形的外心到三角形三边的距离相等. ( )
6.经过弦的中点的直径垂直于弦,且平分弦所对的两条弧. ( )
7.经过圆O内一点的所有弦中,以与OP垂直的弦最短. ( )
8.弦的垂直平分线经过圆心. ( )
9.⊙O的半径是5,弦AB∥CD,AB=6,CD=8,则两弦间的距离是1. ( )
10.在半径是4的圆中,垂直平分半径的弦长是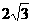 .( )
.( )
11.任意一个三角形一定有一个外接圆且只有一个外接圆. ( )
3.垂径定理:是圆中一个极重要的定理.
垂径定理:垂直于弦的直径平分弦且平分弦所对的两条弦.
推论(1):平分弦(不是直径)的直径垂直于弦,且平分弦所对的两条弦(注意括号内的条件)
(2):弦的垂直平分线经过圆心,并且平分弦所对的两条弧.
(3):平分弦所对的一条弧的直径,垂直平分弦且平分弦所对的另一条弧.
 此定理和三个推论的内容是平分弦,垂直弦是直径平分弧.在这四个条件中满足两个就可得到其它两个的结论.如垂直于弦是直径得到平分弦.平分弧(垂径定理)平分弦,是直径可得到垂直弦.平分弧(推论1)垂直弦,平分弦可得到这条直径是直径,且平分弦(推论2)
此定理和三个推论的内容是平分弦,垂直弦是直径平分弧.在这四个条件中满足两个就可得到其它两个的结论.如垂直于弦是直径得到平分弦.平分弧(垂径定理)平分弦,是直径可得到垂直弦.平分弧(推论1)垂直弦,平分弦可得到这条直径是直径,且平分弦(推论2)
注意:题设是两条,如
 ∵AB是直径
∵AB是直径
AB⊥CD于E
∴CE=DE
弧AC=弧DA 弧BC=弧DB
具体做题时,辅助线往往过圆心做弦的垂线段.连结圆心,则半径,弦的一半,圆心到弦的距离形成一个RtΔ,则可用勾股定理,锐角三角函数进行计算或证明.
2.过一点的圆有无数个,它的圆心是平面上除A外所有点.过两点的圆有无数个,它们的圆心在AB的垂直平分线上.过三点呢?若这三点不在同一直线上,过三点可以做且只可以做一个圆.(但这三点在同一直线上,则不能过三点作圆).
若把三点连结起来,构成三角形,则经过三角形各顶点的圆叫三角形的外接圆.
外接圆的圆心叫三角形外心.外心的性质是到三角形各顶点的距离相等.
三角形的外接圆的做法:作三角形两边的中垂线,两条中垂线的交点是圆心,圆心到顶点的距离是半径.
1.第一自然段主要说明
①圆的概念:此概念有2种解释
1)线段OA绕端点O旋转一周,另一个端点A随之旋转一周,所组成的图形叫圆.
2)到定点的距离等于定长的点的集合.
②圆心,半径,固定端点O叫圆心,OA的长叫半径.
作圆要两个条件:圆心确定圆的位置,圆心确定圆的大小.
③圆内部分:到定点(圆心)的距离小于定长(半径)的点的集合.
圆外部分:到定点(圆心)的距离大于定长(半径)的点的集合.
要确定一个点在圆上,圆外还是圆内,就要计算端点到圆心的距离,计算出距离与半径比较.若该距离d>r,则点在圆外,d=r,在圆上,d<r在圆内.
如⊙O的半径r=5cm,圆心O到直线l的距离d=OP=3cm.在l上有P,Q,R三点,且PD=4cm,QD>4cm,RD<4cm,则P,Q,R三点在⊙O的什么位置.
解:连结OP ∵PD=4cm OD=3cm
 由勾股定理得:OP=5cm OP=r ∴P在⊙O上
由勾股定理得:OP=5cm OP=r ∴P在⊙O上
∵QD>4cm OD=3cm 连结OQ
则OQ2=OP2+QD2>25 ∴OQ>5cm ∴Q在⊙O外
用同样方法证得R在⊙O内.
 ④弦:连结圆上位意两点的线段,
④弦:连结圆上位意两点的线段,
如线段CD
经过圆心的弦叫直径
如AB(直径是圆的最大的弦)
⑤弧:圆上任意两点间的部分,弧若大于半圆叫优弧,小于半圆叫劣弧.

 ⑥弓形:由弦及其所对的弧组成的图形叫
⑥弓形:由弦及其所对的弧组成的图形叫
弓形.弦CD与弧CD及弦CD及优弧CD所有两个弓形.
⑦同心圆:圆心相同,半径不相等的两个圆叫同心圆.
 ⑧能够重合(或半径相等)的两个圆是等圆.
⑧能够重合(或半径相等)的两个圆是等圆.
⑨在同圆或等圆中,能够互相重合的弧叫等弧。
(注意:只要说两弧是等弧,就说明这两段弧在同圆或等圆上)
例1、
已知两圆的半径R,r(R≥r)是方程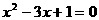 的两个根,两圆的圆心距为d,
的两个根,两圆的圆心距为d,
(1)若d=4,试判定两圆的位置关系;
(2)若d=2,试判定两圆的位置关系;
(3)若两圆相交,试确定d的取值范围;
(4)若两圆相切,求d的值。
解:∵R,r是方程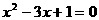 的两根
的两根
∴R+r=3,R·r=1
则 ,
,
(1)∵d=4 ∴d>R+r,则两圆外离;
(2)∵d=2 ∴d<R-r,则两圆内含;
(3)∵两圆相交
∴R-r<d<R+r,即: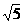 <d<3
<d<3
(4)∵两圆相切
∴d=R+r或d=R-r,即:d=3或d=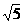
注意:两圆相切有两种可能(内切或外切)
例2:如图(4),⊙o1与⊙o2相交于A、B,直线Ao1交⊙o1于C,交⊙o2于D,CB的延长线交⊙o2于E,若CD=10,DE=6,求⊙o2的长。
解:连结AB、AE
 AC为⊙o1的直径
AC为⊙o1的直径




ABCD内接于⊙o2

AE为⊙o2的直径 o2为AE中点
o2为AE中点 



o1为AC中点
在 中,
中,


CD=10,DE=6
注意:两圆相交时,常添公共弦、连心线等作为辅助线,这些辅助线能把两圆中的角或线段联系起来,起到“桥梁”作用。
例3:
如图(5),⊙o1与⊙o2相交于A、B,CE切⊙o1于C,交⊙o2于D、E
求证:
分析:因 ,所以只需证
,所以只需证
 ,联想到两圆相交时常添的辅助线,再运用弦切角定理及圆内接四边形性质,问题易得证。
,联想到两圆相交时常添的辅助线,再运用弦切角定理及圆内接四边形性质,问题易得证。
证:连结AB
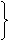 CD切⊙o1于C
CD切⊙o1于C
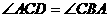


BEDA内接于⊙o2
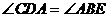
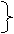





注意:如果⊙o1的切线CE与⊙o2也相切于E(D、E重合),则
 成立吗?
成立吗?
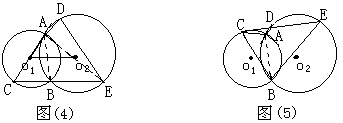
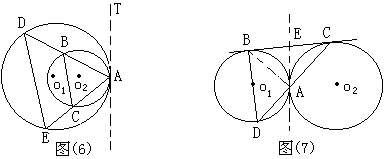
例4:如图(6),⊙o1与⊙o2内切于A,过A作大圆的弦AD、AE分别交小圆于B、C。求证: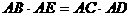
分析:要证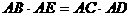 ,只需证
,只需证 ,即要证BC∥DE;
,即要证BC∥DE;
证明:过点A作⊙o1与⊙o2的公切线AT,则:
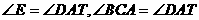
∵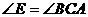 ∴BC∥DE
∴BC∥DE
∴ ,即:
,即: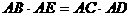
例5:如图(7),⊙o1与⊙o2外切于A,BC分别切⊙o1和⊙o2于B、C,CA交⊙o1于D,求证:
证明:过点A作⊙o1、⊙o2的公切线AE交BC于E,连结AB

 EB、EA为⊙o1的切线
EB、EA为⊙o1的切线 EB=EA
EB=EA  EC=EB=EA
EC=EB=EA

同理:EC=EA
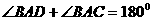
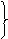


 BD为⊙o1的直径
BD为⊙o1的直径 


BC为⊙o1的切线 

 ∽
∽
注意:当两圆外切线内切时,公切线是常添的辅助线。
例6:如图(8),两圆内切于点C,⊙o1的弦AB切⊙o2于E,CE的延长线交⊙o1于点D,求证:
分析:要证
只须证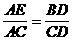 ,即要证
,即要证 ∽
∽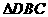 ,因两圆内切,所以可过点C作
,因两圆内切,所以可过点C作
公切线MN,从而证得: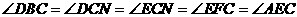
又因为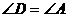 ,从而问题得以解决。
,从而问题得以解决。
证明:过点C作⊙o1与⊙o2的公切线MN,连结EF、AC,
则有: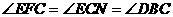
又∵AB为⊙o2的切线, ∴
∴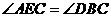
又∵
∴ ∽
∽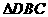 ∴
∴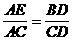
即:

注:本讲内容较多,例题也比较详细、全面,因此不再单独设立练习题。
5、 当两圆相交、外切、外离时,总有两条外公切线,且这两条外公切线长相等。如果两圆相等,那么两条外公切线平行;如果两圆不等,那么两条外公切线相交,且交点在两圆的连心线上。当两圆相切时,常作两圆的公切线为辅助线。
4、求两圆的内、外公切线长的问题,都是利用直线和圆相切的性质,通过作出过切点的半径,把问题转化为解一个直角三角形。
在图(2)、图(3)中,o1o2=d,⊙o1半径为R,⊙o2的半径为r,则在 中:
中:
图(2):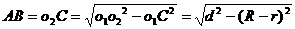
图(3):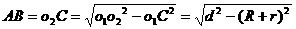
当两圆外切时,d=R+r,此时
外公切线长=
3、 两圆的五种位置关系中,重点讨论了两圆相交、相切的性质,在解决两圆的相交问题时,如图(1),常添连心线、公共弦等辅助线,这样,两圆半径、圆心距、公共弦长的一半就集中到了
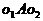 中,可以利用三角形有关知识加以解决。
中,可以利用三角形有关知识加以解决。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com