
题目列表(包括答案和解析)
4. 方程x(x+3)=x+3的解是 ( )
A. x=1 B. x1=0, x2=-3
C. x1=1, x2=3 D. x1=1, x2=-3
3.小明的妈妈为了奖励小明在学习中取得的进步,给小明新买了一个文具盆,你估计这个文具盒的厚度为3( )(填上合适的长度单位)。
A.mm; B.cm; C.dm; D.km
2.化简x-y-(x+y)的最后结果是( )
A.0 B.2x C.-2y D.2x-2y
1.计算2-(-1)2等于( )
A.1 B.0 3.-1 D.3
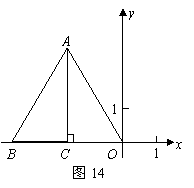
18.如图14,在平面直角坐标系中,两个全等的直角三角形的直角顶点及一条直角边重合,点 在第二象限内,点B,点C在x轴的负半轴上,∠CAO=30°OA=4.
在第二象限内,点B,点C在x轴的负半轴上,∠CAO=30°OA=4.
(1)求点C的坐标;
(2)如图15,将△ABC绕点C按顺时针方向旋转30°到△A’ CB’的位置,其中A’C交直线OA于点E,A’B’分别交直线OA,CA于点F,G,则除△A’B’C≌△AOC外,还有哪几对全等的三角形,请直接写出答案;(不再另外添加辅助线)
(3)在(2)的基础上,将A’CB’绕点C按顺时针方向继续旋转,当△COE的面积为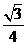 时,求直线CE的函数表达式.
时,求直线CE的函数表达式.
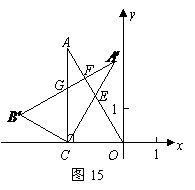
17.如图10,在正方形ABCD中,点E,F分别为边BC,CD的中点,AF,DE相交于点G,则可得结论:①AF=DE;②AF⊥DE.(不需要证明)
(1)如图11,若点E,F不是正方形ABCD的边BC,CD的中点,但满足CE=DF,则上面的结论①,②是否仍然成立?(请直接回答“成立”或“不成立”)
(2)如图12,若点E,F分别在正方形ABCD的边CB的延长线和DC的延长线上,且CE=DF,此时上面的结论1,2是否仍然成立?若成立,请写出证明过程,若不成立,请说明理由.
(3)如图13,在(2)的基础上,连接AE和EF,若点M,N,P,Q分别为AE,EF,FD,AD的中点,请判断四边形MNPQ是“矩形、菱形、正方形、等腰梯形”中的哪一种?并写出证明过程.

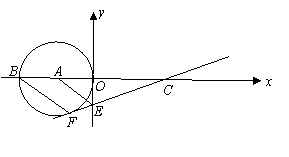
16.如图,已知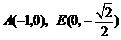 ,以点A为圆心,以AO长为半径的圆交
,以点A为圆心,以AO长为半径的圆交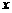 轴于另一点B,过点B作BF∥AE交⊙A于点F,直线FE交x轴于点C.
轴于另一点B,过点B作BF∥AE交⊙A于点F,直线FE交x轴于点C.
(1)求证:直线FC是⊙a的切线;
(2)求点C的坐标及直线FC的解析式;
 (3)有一个半径与⊙A的半径相等,且圆心在
(3)有一个半径与⊙A的半径相等,且圆心在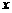 轴上运动的⊙P.若⊙P与直线FC相交于M,N两点,是否存在这样的点P,使△PMN是直角三角形.若存在,求出点P的坐标;若不存在,请说明理由.
轴上运动的⊙P.若⊙P与直线FC相交于M,N两点,是否存在这样的点P,使△PMN是直角三角形.若存在,求出点P的坐标;若不存在,请说明理由.
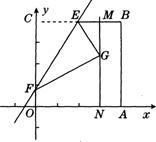
15.如图,四边形OABC是一张放在平面直角坐标系中的正方形纸片.点O与坐标原点重合,点A在x轴上,点C在y轴上,OC=4,点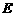 为BC的中点,点
为BC的中点,点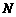 的坐标为
的坐标为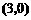 ,过点
,过点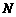 且平行于
且平行于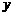 轴的直线MN与EB交于点M.现将纸片折叠,使顶点C落在MN上,并与MN上的点G重合,折痕为EF,点F为折痕与y轴的交点.
轴的直线MN与EB交于点M.现将纸片折叠,使顶点C落在MN上,并与MN上的点G重合,折痕为EF,点F为折痕与y轴的交点.
(1)求点G的坐标;
(2)求折痕EF所在直线的解析式;
(3)设点P为直线EF上的点,是否存在这样的点P,使得以P、F、G为顶点的三角形为等腰三角形,若存在,请直接写出点P的坐标;若不存在,请说明理由.
14.已知BC为⊙O直径,D是直径BC上一动点(不与点B,O,C重合),过点D作直线AH⊥BC交⊙O于A,H两点,F是⊙O上一点(不与点B,C重合),且︵AB=︵AF,直线BF交直线AH于点E.
(1)如图(a),当点D在线段BO上时,试判断AE与BE的大小关系,并证明你的结论;
(2)当点D在线段OC上,且OD>DC时,其它条件不变.
①请你在图(b)中画出符合要求的图形,并参照图(a)标记字母;
②判断(1)中的结论是否还成立,请说明理由.

13.如图,某人在山坡坡脚 处测得电视塔尖点
处测得电视塔尖点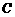 的仰角为
的仰角为 ,沿山坡向上走到
,沿山坡向上走到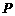 处再测得点C的仰角为
处再测得点C的仰角为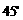 ,已知OA=100米,山坡坡度
,已知OA=100米,山坡坡度 且O,A,B在同一条直线上.求电视塔OC的高度以及此人所在位置点
且O,A,B在同一条直线上.求电视塔OC的高度以及此人所在位置点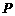 的铅直高度.(测倾器高度忽略不计,结果保留根号形式)
的铅直高度.(测倾器高度忽略不计,结果保留根号形式)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com