
题目列表(包括答案和解析)
8、(1) 连接O2B
易证四边形ADO2B 为矩形,在Rt⊿O2DO1 中,
O1D=2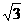 ,O1O2=4
,O1O2=4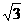 ,则 ∠O1O2D=300 ,O2D=6
,则 ∠O1O2D=300 ,O2D=6
(2)由(1)得AB= O2D=6,∴点C的坐标为(0,3)
(3)由图知:O1、O2 点的坐标为(-3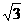 ,0)、(
,0)、(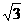 ,0)
,0)
设过点O1、O2 、C三点的抛物线的解析式为y=ax2+bx+c
则有: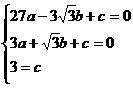
解之得:a=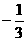 b=
b= 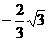 c=3
c=3
故抛物线的解析式为:y=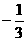 x2+
x2+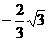 x+3
x+3
(4)
存在,点C显然满足条件,又根据抛物线的对称性知,点C关于x=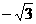 的对称点也满足条件,即P点的坐标为(0,3)、(
的对称点也满足条件,即P点的坐标为(0,3)、(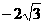 ,3)
,3)
7、 (1) AC=15 BC=20
(2)∵ S△ABC=AC·BC=OC·AB, ∴ OC=12
∴ PO+PC=4+2k=12. ∴ k=4
∴ 方程可化为x2-12x+32=O.解得x1=4,x2=8
∵ PO<PC. ∴ PO=4. ∴ P(O,-4)
(3)存在,直线PQ解析式为:y=-x-4或y=- x -4
6、(1) a=-1 , k=1
k=1
(2)在二次函数y=-x2+2x+3的图像上存在点P,
使得ΔPBC是以BC为一条直角边的直角三角形
①由 (1)可知,直线y=x+3与x轴的交点为E(-3,0)
 OE=OC=3
OE=OC=3 ∠CEO=450 ,
∠CEO=450 , ∠OBC=450
∠OBC=450 ∠ECB=900
∠ECB=900 ∠DCB=900
∠DCB=900
 ΔDCB是以BC为一条直角边的直角三角形,
ΔDCB是以BC为一条直角边的直角三角形,
且点D(1,4)在二次函数的图像上,则点D是所求的P点
方法一:设∠CBP=900,点P在二次函数y=-x2+2x+3的图像上,
则ΔPBC是以BC为一条直角边的直角三角形,
 ∠CBO=450
∠CBO=450  ∠OBP=450
∠OBP=450
设直线BP与y轴交于点F,则F(0,-3) 直线BP的表达式为y=x-3
直线BP的表达式为y=x-3
解方程组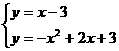 得
得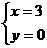 或
或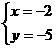
由题意得,点P(-2,-5)为所求。
综合①②,得二次函数y-x2+2x+3的图像上存在点P(1,4)或
P(-2,-5),使得ΔPBC是以BC为一条直角边的直角三角
方法二:在y轴上取一点F(0,-3),则OF=OC=3,由对称性可知,∠OBF=∠OBC=450
 ∠CBF=900
∠CBF=900
设直线BF与二次函数y=-x2+2x+3的图像交于点P,由(1)知B(3,0),
 直线BF的函数关系式为y=x-3(以下与方法一同)
直线BF的函数关系式为y=x-3(以下与方法一同)
5、⑴C(2a,0),D(0,2a+8)
⑵方法一:由题意得:A(-4,0),B(0,4)
-4<a<0,且a≠2,
① 当2a+8<4,即-4<a<-2时AC=-4-2a,BD=4-(2a+8)=-4-2a
∴AC=BD。当2a+8>4,即-2<a<0时,同理可证:AC=BD
综上:AC=BD
方法二:①当点D在B、O之间时,连CD,∵∠COD=90°
∴圆心M在CD上,过点D作DF∥AB,∵点M为CD中点,
∴MA为△CDF中位线,∴AC=AF,
又DF∥AB,∴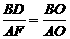 ,而BO=AO ∴AF=BD ∴AC=BD
,而BO=AO ∴AF=BD ∴AC=BD
②点D在点B上方时,同理可证:AC=BD,综上:AC=BD
⑶方法一
①A(-4,0),B(0,4),D(0,2a+8),M(a,a+4),△BDE、△ABO均为等腰直角三角形,
E的纵坐标为a+6,∴ME=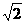 (yE-yM)=
(yE-yM)=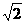 [a+6-(a+4)]=2
[a+6-(a+4)]=2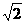 ,AB=4
,AB=4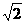 ∴AB=2ME
∴AB=2ME
② AM=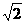 ( yM-yA)=
( yM-yA)=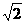 (a+4),BE=
(a+4),BE=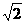 |yE-yB|=
|yE-yB|=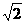 |a+2|,
|a+2|,
∵AM=BE又-4<a<0,
且a≠2,10 当-4<a<-2时,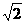 (a+4)= -
(a+4)= -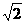 (a+2) ∴a=-3,M(-3,1)
(a+2) ∴a=-3,M(-3,1)
20 当-2<a<0时,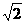 (a+4)=
(a+4)= 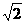 (a+2)
(a+2)
∴a不存在
4、解:(1)yB=5=半径; 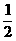 xCyC=
xCyC=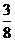
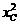 ,
, 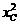 +y2C=25, 得C (4,3) …2分和C(4,-3)
+y2C=25, 得C (4,3) …2分和C(4,-3)
(2)①过点P(4,3)、Q(3,5)的抛物线y=a0x2+h0
即为y=-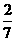 x2+
x2+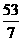 ,得h0=
,得h0=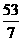 .
.
过P1(p+1,3)、Q1(p,5)的抛物线y=a1x2+h1
即为y=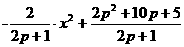 ,
,
h1=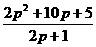 .h0-h1=
.h0-h1=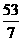 -
-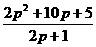 =
=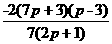
=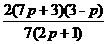 ,
,
(∵MQ>M1Q1,其中MQ=6,∴0≤p=1/2M1Q1<3,)可知0≤p<3;
∴7p+3>0,2p+1>0,3-p>0,因而得到h0-h1>0,证得h0>h1.
(或者说明2p+1>0,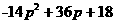 在0≤p<3时总是大于0,得到h0-h1>0.
在0≤p<3时总是大于0,得到h0-h1>0.
②显然抛物线y=ax2+bx+c的开口方向向下,a<0.
当T运动到B点时,这时B、T、K三点重合即B为抛物线的顶点,∴yK≥5;
将过点T、B、C三点的抛物线y=ax2+bx+c沿x轴平移,使其对称轴为y轴,这时yK不变.
则由上述①的结论,当T在FB上运动时,过F(-3,5)、B(3,5)、C(4,3)三点的抛物线的顶点为最高点,
∴yK≤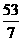 , ∴ 5≤yK≤
, ∴ 5≤yK≤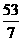
3、


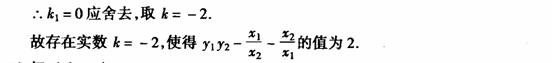
2. (1)A(1,2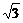 )E(0,
)E(0,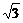 )
)
(2)y=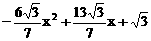 (3)(
(3)(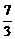 ,
,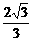 ),2
),2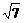 +2,
+2,
1、(1)由旋转的性质可知:OC=OA=2,OD=OB=4
∴C、D两点的坐标分别为C(-2,0)、D(0,4)
(2)所求抛物线的解析式为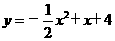 。
。
(3)答:△PMB是钝角三角形。
如图,PH是抛物线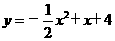 的对称轴,
的对称轴,
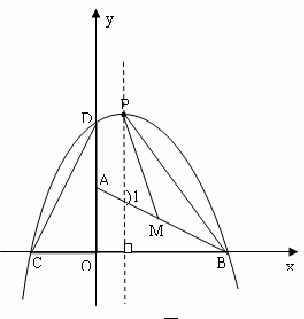
求得M、P两点的坐标分别为M(2,1),P(1,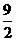 ).
).
∴点M在PH右侧,
又∵∠PHB=90° ∴∠1>90°
∵∠PMB>∠1 ∴△PMB是钝角三角形。
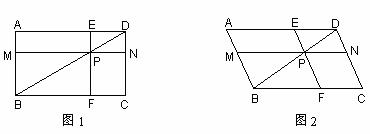
9、(2005年重庆)(10分)已知四边形ABCD中,P是对角线BD上的一点,过P作MN∥AD,EF∥CD,分别交AB、CD、AD、BC于点M、N、E、F,设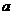 =PM·PE,
=PM·PE,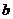 =PN·PF,解答下列问题:
=PN·PF,解答下列问题:
(1)当四边形ABCD是矩形时,见图1,请判断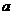 与
与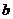 的大小关系,并说明理由;
的大小关系,并说明理由;
(2)当四边形ABCD是平行四边形,且∠A为锐角时,见图2,(1)中的结论是否成立?并说明理由;
(3)在(2)的条件下,设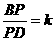 ,是否存在这样的实数
,是否存在这样的实数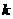 ,使得
,使得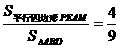 ?若存在,请求出满足条件的所有
?若存在,请求出满足条件的所有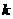 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
能力训练答案:
8、(2005年恩施)年如图,在平面直角坐标系中,半径分别为3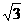 和
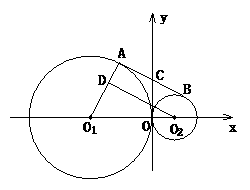
和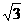 的⊙O1和⊙O2外切于原点O,在x轴上方的两圆的外公切线AB与⊙O1和⊙O2分别切于点A、B,直线AB交y轴于点C.O2D⊥O1A于点D.
的⊙O1和⊙O2外切于原点O,在x轴上方的两圆的外公切线AB与⊙O1和⊙O2分别切于点A、B,直线AB交y轴于点C.O2D⊥O1A于点D.
(1)求∠O1O2D的度数;
(2)求点C的坐标;
(3)求经过O1、C、O2三点的抛物线的解析式;
(4)在抛物线上是否存在点P,使⊿PO1O2为直角三角形.若存在,求出点P的坐标; 若不存在,请说明理由.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com