
题目列表(包括答案和解析)
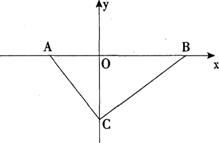
7、(2005年黑龙江)如图,在平面直角坐标系中,Rt△ABC的斜边AB在x轴上,AB=25,顶点C在y轴的负半轴上,tan∠ACO=,点P在线段OC上,且PO、PC的长(PO<PC)是关于x的方程x2-(2k+4)x+8k=O的两根.
(1)求AC、BC的长;
(2)求P点坐标;
(3)在x轴上是否存在点Q,使以点A、C、P、Q为顶点的四边形是梯形?若存在,请直接写出直线PQ的解析式;若不存在,请说明理由.
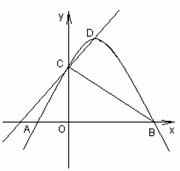
6、(2005年茂名)知二次函数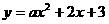 的图像与x轴交于点A、点B(点B在X轴的正半轴上),与y轴交于点C,其顶点为D,直线DC的函数关系式为
的图像与x轴交于点A、点B(点B在X轴的正半轴上),与y轴交于点C,其顶点为D,直线DC的函数关系式为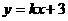 ,又tan∠OBC=1,
,又tan∠OBC=1,
(1) 求a、k的值;
(2)
 探究:在该二次函数的图像上是否存在点P(点P与点B、C补重合),使得ΔPBC是以BC为一条直角边的直角三角形?若存在,求出点P的坐标,若不存在,请你说明理由
探究:在该二次函数的图像上是否存在点P(点P与点B、C补重合),使得ΔPBC是以BC为一条直角边的直角三角形?若存在,求出点P的坐标,若不存在,请你说明理由
5、(2005年淮安)知直线y=x+4与x轴、y轴分别相交于点A、B,点M是线段AB(中点除外)上的动点,以点M为圆心,OM的长为半径作圆,与x轴、y轴分别相交于点C、D.
(1)设点M的横坐标为a,则点C的坐标为 ,点D的坐标为 (用含有a的代数式表示);
(2)求证:AC=BD;
(3)若过点D作直线AB的垂线,垂足为E.
①求证: AB=2ME;
②是否存在点M,使得AM=BE?若存在,求出点M的坐标;若不存在,请说明理由.
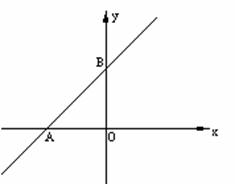
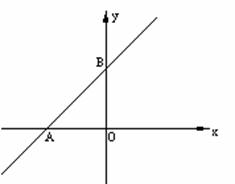
4.(2005年宜昌)以原点O为圆心、5为半径的半圆与y轴交于A、G两点,AB与半圆相切于点A,点B的坐标为(3,yB)(如图1);过半圆上的点C(xC,yC)作y轴的垂线,垂足为D;Rt△DOC的面积等于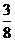
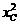 .
.
(1)求点C的坐标;
(2)①命题“如图2,以y轴为对称轴的等腰梯形MNPQ与M1N1P1Q1的上底和下底都分别在同一条直线上,NP∥MQ,PQ∥P1Q1 ,且NP>MQ.设抛物线y=a0x2+h0过点P、Q,抛物线y=a1x2+h1过点P1、Q1,则h0>h1”是真命题.请你以Q(3,5)、P(4,3)和Q1(p,5)、P1(p+1,3)为例进行验证;
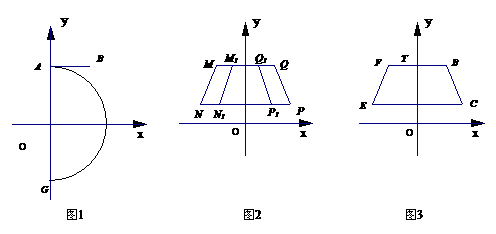 ②当图1中的线段BC在第一象限时,作线段BC关于y轴对称的线段FE,连接BF、CE,点T是线段BF上的动点(如图3);设K是过T、B、C三点的抛物线y=ax2+bx+c的顶点,求K的纵坐标yK的取值范围.
②当图1中的线段BC在第一象限时,作线段BC关于y轴对称的线段FE,连接BF、CE,点T是线段BF上的动点(如图3);设K是过T、B、C三点的抛物线y=ax2+bx+c的顶点,求K的纵坐标yK的取值范围.
3.(2005年四川)已知关于x、y的方程组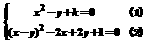 有两个不相同的实数解。
有两个不相同的实数解。
(1)求实数k的取值范围;
(2)若 和
和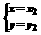 是方程组的两个不相同的实数解,是否存在实数k,使得yly2―
是方程组的两个不相同的实数解,是否存在实数k,使得yly2― ―
―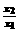 的值等于2;若存在,求出k的值;若不存在,请说明理由。
的值等于2;若存在,求出k的值;若不存在,请说明理由。
2.(2005年深圳)已知△ABC是边长为4的等边三角形,BC在x轴上,点D为BC的中点,点A在第一象限内,AB与y轴的正半轴相交于点E,点B(-1,0),P是AC上的一个动点(P与点A、C不重合)
(1)求点A、E的坐标;
(2)若y= 过点A、E,求抛物线的解析式。
过点A、E,求抛物线的解析式。
(3)连结PB、PD,设L为△PBD的周长,当L取最小值时,求点P的坐标及L的最小值,并判断此时点P是否在(2)中所求的抛物线上,请充分说明你的判断理由。
1.(2005年陕西)如图,在直角坐标系中,Rt△AOB的顶点坐标分别为A(0,2),O(0,0),B(4,0),△AOB绕O点按逆时针方向旋转90°得到△COD.
(1) 求C、D两点的坐标;
(2) 求经过C、D、B三点的抛物线的解析式;
(3)  设(2)中的抛物线的顶点为P,AB的中点为M,试判断△PMB是钝角三角形、直角三角形还是锐角三角形,并说明理由。
设(2)中的抛物线的顶点为P,AB的中点为M,试判断△PMB是钝角三角形、直角三角形还是锐角三角形,并说明理由。
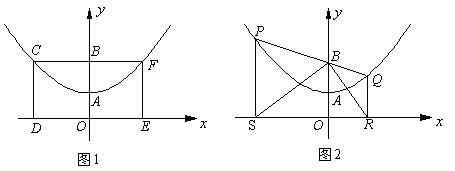
5、(2005年临沂)如图1,已知抛物线的顶点为A(0,1),矩形CDEF的顶点C、F在抛物线上,D、E在x轴上,CF交y轴于点B(2,0),且其面积为8。
⑴求此抛物线的解析式;
⑵如图2,若P点为抛物线上不同于A的一点,连结PB并延长交抛物线于点Q,过点P、Q分别作x轴的垂线,垂足分别为S、R。
①求证:PB=PS;
②判断△SBR的形状;
③试探索在线段SR上是否存在点M,使得以点A、S、M为顶点的三角形和以点Q、R、M为顶点的三角形相似,若存在,请找出M点的位置;若不存在,请说明理由。
能力训练
4、(2005年金华)如图,抛物线y=ax2+bx+c经过点O(0,0),A(4,0),B(5,5).点C是y轴负半轴上一点,直线l经过B,C两点,且tan∠OCB=.
(1)求抛物线的解析式;
(2)求直线l的解析式;
 (3)过O,B两点作直线,如果P是直线OB上的一个动点,过点P作直线PQ平行于y轴,交抛物线于点Q. 问:是否存在点P,使得以P,Q,B 为顶点的三角形与△OBC相似?如果存在,请求出点P的坐标;如果不存在,请说明理由.
(3)过O,B两点作直线,如果P是直线OB上的一个动点,过点P作直线PQ平行于y轴,交抛物线于点Q. 问:是否存在点P,使得以P,Q,B 为顶点的三角形与△OBC相似?如果存在,请求出点P的坐标;如果不存在,请说明理由.
3、(2005年哈尔滨)已知:直线y=2x+6与x轴和y轴分别交于A、C两点,抛物线y=-x2+bx+c经过点A、C,点B是抛物线与x轴的另一个交点。
(1)求抛物线的解析式及点B的坐标;
(2)设点P是直线AC上一点,且S△ABP∶S△BPC=1∶3,求点P的坐标;
 (3)直线y=
(3)直线y=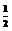 x+a与(1)中所求的抛物线交于M、N两点,问:是否存在a的值,使得∠MON=90º,若存在,求出a的值;若不存在,请说明理由。
x+a与(1)中所求的抛物线交于M、N两点,问:是否存在a的值,使得∠MON=90º,若存在,求出a的值;若不存在,请说明理由。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com