1．计算：(sin30°)·(tan60°)-1＝______．

22. (本题满分12分)

　　 把两个全等的等腰直角三角形ABC和EFG(其直角边长均为4)叠放在一起(如图①)，且使三角板EFG的直角顶点G与三角板ABC的斜边中点O重合.现将三角板EFG绕O点顺时针旋转(旋转角α满足条件：0°＜α＜90°)，四边形CHGK是旋转过程中两三角板的重叠部分(如图②)

　　 (1)在上述旋转过程中，BH与CK有怎样的数量关系？四边形CHGK的面积有何变化？证明你发现的结论；

(2)连接HK，在上述旋转过程中，设BH=，△GKH的面积为，求与之间的函数关系式，并写出自变量的取值范围；

(3)在(2)的前提下，是否存在某一位置，使△GKH的面积恰好等于△ABC面积的？若存在，求出此时的值；若不存在，说明理由。

21. (本题满分12分)

　 　如图，A、B是直线上的两点，AB＝4厘米，过外一点C作CD∥，射线BC与所成的锐角∠l＝60°，线段BC＝2厘米。动点P，Q分别从B，C同时出发，P以每秒1厘米的速度沿由B向C的方向运动，Q以每秒2厘米的速度沿由C向D的方向运动．设P，Q运动的时间为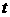(秒)，当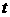＞2时，PA交CD于E。

　　 (1)用含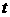的代数式分别表示CE和QE的长；

　　 (2)求△APQ的面积S与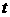的函数关系式；

(3)当QE恰好平分△APQ的面积时，QE的长是多少厘米？

20. (本题满分10分)

　　 某瓜果基地市场为指导该基地某种蔬菜的生产和销售，对往年的市场行情和生产情况进行了调查，提供了如下两个信息图，如甲、乙两图：

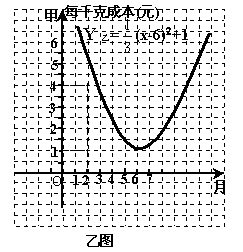
　　 (1)在3月份出售这种蔬菜，每千克的收益是多少元？(收益＝售价－成本)

(2)哪个月出售这种蔬菜，每千克的收益最大？说明理由。

19. (本题满分10分)

　　 如图，△ABC中，∠ACB=90°，D为AB中点，四边形BCED为平行四边形，DE、AC相交于点F。求证：

　　 (1)点F为AC中点；

　　 (2)试确定四边形ADCE的形状，并说明理由；

　　 (3)若四边形ADCE为正方形，△ABC应添加什么条件，并证明你的结论.

18. (本题满分8分)

　　 某学校打算假期组织老师外出旅游，初步统计，参加旅游的人数约在30-60人左右. 该校联系了两家报价均为1200元的旅行社，甲旅行社的优惠措施是30人以内(包括30人)全额收费，超出部分每人打六折；乙旅行社的优惠措施是每人打九折，若人数在30人(包括30人)以上，还可免去两个人的费用

　　 (1)该校选择哪一家旅行社合算？

(2)若该校最终确定参加旅游的人数为48人，学校可给每位参加旅游的教师补贴200元，则参加旅游的教师每人至少要花多少钱？

17. (本题满分8分)

　　 某船以20海里/时的速度将一批重要物资由A处运往正西方向的B处，经16小时的航行到达，到达后立即卸货，此时，接到气象部门通知，一台风中心正以40海里/时的速度由A向北偏西60⁰的方向移动，距台风中心200海里的圆形区域(包括边界)均会受到影响。

　　 (1)B处是否会受到台风的影响？请说明理由；

　　 (2)为避免受到台风影响，该船应在多少小时内卸完货物？(=1.7，结果保留一位小数)

16. (本题满分6分)

　　 下面是两个转盘，每个转盘分成几个相等的扇形，甲、乙两个人做游戏，游戏者同时转动两个转盘一次，如果转盘A转出了红色，转盘B转出了蓝色，则甲赢否则乙赢.

　　 (1)甲和乙获胜的概率分别是多少？

　　 (2)这个游戏对双方公平吗？说说你的理由.

　　 (3)如果你认为不公平，应怎样修改才能使游戏对双方公平

15. (本题满分6分)

　　 为了让学生了解环保知识，增强环保意识，某中学举行了一次“环保知识竞赛”，共有900名学生参加了这次竞赛。为了解本次竞赛成绩情况，从中抽取了部分学生的成绩(得分取正整数，满分为100分)进行统计，请你根据下面尚未完成并有局部污损的频率分布表和频率分布直方图，解答下列问题：

　　 (1)填充频率分布表中的空格；

　　 (2)补全频率分布直方图；

　　 (3)在该问题中共抽查了_______名学生？

　　 (4)全体参赛学生中，竞赛成绩落在_____________(填范围)的人数最多？

　　 (5)若成绩在90分以上(不含90分)为优秀，则该校成绩达到优秀的约为________人。

14. (本题满分6分)

　　 解下列方程：