
题目列表(包括答案和解析)
2、(2005年北京市)已知:在平面直角坐标系xOy中,一次函数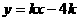 的图象与x轴交于点A,抛物线
的图象与x轴交于点A,抛物线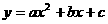 经过O、A两点。
经过O、A两点。
(1)试用含a的代数式表示b;
(2)设抛物线的顶点为D,以D为圆心,DA为半径的圆被x轴分为劣弧和优弧两部分。若将劣弧沿x轴翻折,翻折后的劣弧落在⊙D内,它所在的圆恰与OD相切,求⊙D半径的长及抛物线的解析式;
(3)设点B是满足(2)中条件的优弧上的一个动点,抛物线在x轴上方的部分上是否存在这样的点P,使得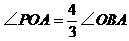 ?若存在,求出点P的坐标;若不存在,请说明理由。
?若存在,求出点P的坐标;若不存在,请说明理由。
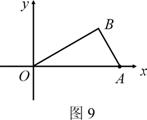
1.(2005年资阳市).如图9,已知O为坐标原点,∠AOB=30°,∠ABO=90°,且点A的坐标为(2,0).
(1) 求点B的坐标;
(2) 若二次函数y=ax2+bx+c的图象经过A、B、O三点,求此二次函数的解析式;
(3) 在(2)中的二次函数图象的OB段(不包括点O、B)上,是否存在一点C,使得四边形ABCO的面积最大?若存在,求出这个最大值及此时点C的坐标;若不存在,请说明理由.
5、(2005年无锡)已知,点P是正方形ABCD内的一点,连PA、PB、PC.
(1)将△PAB绕点B顺时针旋转90°到△P′CB的位置(如图1).
①设AB的长为a,PB的长为b(b<a),求△PAB旋转到△P′CB的过程中边PA所扫过区域(图1中阴影部分)的面积;
②若PA=2,PB=4,∠APB=135°,求PC的长.
(2)如图2,若PA2+PC2=2PB2,请说明点P必在对角线AC上.


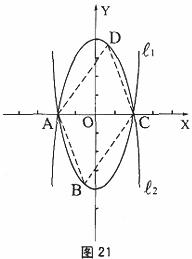
例2(2005年玉溪)如图21,已知抛物线 的图象与x轴交于A、C两点。
的图象与x轴交于A、C两点。
(1)若抛物线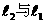 关于x轴对称,求
关于x轴对称,求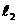 的解析式;(3分)
的解析式;(3分)
(2)若点B是抛物线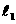 上一动点(B不与A、C重合),以AC为对角线,A、B、C三点为顶点的平行四边形的第四个顶点记为D,求证:点D在
上一动点(B不与A、C重合),以AC为对角线,A、B、C三点为顶点的平行四边形的第四个顶点记为D,求证:点D在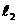 上;(4分)
上;(4分)
(3)探索:当点B分别位于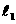 在x轴上、下两部分的图象上时,□ABCD的面积是否存在最大值或最小值?若存在,判断它是何种特殊平行四边形并求出它的面积;若不存在,请说明理由。(4分)
在x轴上、下两部分的图象上时,□ABCD的面积是否存在最大值或最小值?若存在,判断它是何种特殊平行四边形并求出它的面积;若不存在,请说明理由。(4分)
解:
(1)设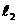 的解析式为y=
的解析式为y=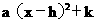 .
.
∵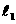 与x轴的交点A(-2,0),C(2,0),顶点坐标是(0,-4),
与x轴的交点A(-2,0),C(2,0),顶点坐标是(0,-4),
并且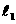 与
与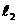 关于x轴对称,
关于x轴对称,
∴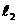 经过点A(-2,0),C(2,0),顶点坐标是(0,4)
经过点A(-2,0),C(2,0),顶点坐标是(0,4)
∴y=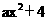 .
∴0=4a+4 得a=-1,
.
∴0=4a+4 得a=-1,
∴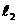 的解析式为
的解析式为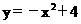 .
.
(2)设B(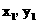 ) ∵点B在
) ∵点B在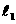 上,∴B(
上,∴B(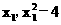 )
)
∵四边形ABCD是平行四边形,A、C关于O对称。∴B、D关于原点O对称,
∴D(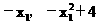 ).
).
将D(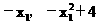 )的坐标代入
)的坐标代入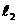 :
: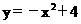
可知 左边=右边。∴点D在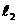 上。
上。
(3)设□ABCD的面积为S,则S=2×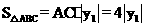 .
.
(I)当点B在x轴上方时,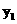 >0,
>0,
∴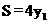 ,它是关于
,它是关于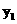 的正比例函数且S随
的正比例函数且S随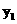 的增大而增大,
的增大而增大,
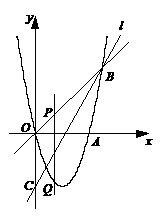 ∴S既无最大值也无最小值。
∴S既无最大值也无最小值。
(II)当点B在x轴下方时,-4≤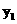 <0.
<0.
∴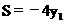 ,它是关于
,它是关于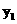 的正比例函数且S随
的正比例函数且S随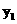 的增大而减小,
的增大而减小,
∴当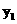 =-4时,S有最大值16,但它没有最小值。
=-4时,S有最大值16,但它没有最小值。
此时B(0,-4)在y轴上,它的对称点D也在y轴上。
∴AC⊥BD.∴□ABCD是菱形。此时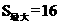 .
.
说明:考查了轴对称的有关性质,一次函数和二次函数的解析式的求法及它们性质的应用,还考查了平行四边形、菱形的判定及性质应用。
练习二
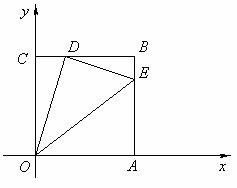
4、(2005年浙江)如图,边长为1的正方形OABC的顶点O为坐标原点,点A在x轴的正半轴上,点C在y轴的正半轴上.动点D在线段BC上移动(不与B,C重合),连接OD,过点D作DE⊥OD,交边AB于点E,连接OE.记CD的长为t.
(1) 当t=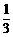 时,求直线DE的函数表达式;
时,求直线DE的函数表达式;
(2) 如果记梯形COEB的面积为S,那么是否存在S的最大值?若存在,请求出这个最大值及此时t的值;若不存在,请说明理由;
(3) 当OD2+DE 2的算术平方根取最小值时,求点E的坐标.
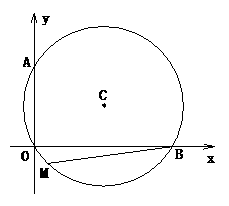
3、(2005年辽宁)如图,⊙C经过坐标原点O,分别交x轴正半轴、y轴正半轴于点B、A,点B的坐标为(4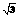 ,0),点M在⊙C上,并且∠BMO=120º。
,0),点M在⊙C上,并且∠BMO=120º。
(1)求直线AB的解析式;
(2)若点P是⊙C上的点,过点P作⊙C的切线PN,若∠NPB=30º,求点P的坐标;
(3)若点D是⊙C上任意一点,以B为圆心,BD为半径作⊙B,并且BD的长为正整数。
①问这样的圆有几个?它们与⊙C有怎样的位置关系?
②在这些圆中,是否存在与⊙C所交的弧(指⊙B上的一条弧)为90º的弧,若存在,请给出证明;若不存在,请说明理由。
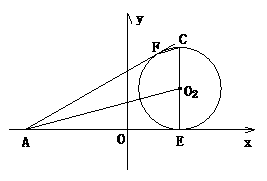
2、(2005年武汉)如图,在平面直角坐标系中,点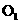 的坐标为(-4,0),以点
的坐标为(-4,0),以点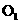 为圆心,8为半径的圆与x轴交于A、B两点,过点A作直线l与x轴负方向相交成60°角。以点
为圆心,8为半径的圆与x轴交于A、B两点,过点A作直线l与x轴负方向相交成60°角。以点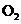 (13,5)为圆心的圆与x轴相切于点D.
(13,5)为圆心的圆与x轴相切于点D.
(1)求直线l的解析式;
(2)将⊙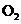 以每秒1个单位的速度沿x轴向左平移,同时直线l沿x轴向右平移,当⊙
以每秒1个单位的速度沿x轴向左平移,同时直线l沿x轴向右平移,当⊙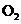 第一次与⊙
第一次与⊙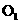 相切时,直线l也恰好与⊙
相切时,直线l也恰好与⊙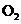 第一次相切,求直线l平移的速度;
第一次相切,求直线l平移的速度;
(3)将⊙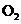 沿x轴向右平移,在平移的过程中与x轴相切于点E,EG为⊙
沿x轴向右平移,在平移的过程中与x轴相切于点E,EG为⊙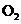 的直径,过点A作⊙
的直径,过点A作⊙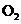 的切线,切⊙
的切线,切⊙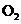 于另一点F,连结A
于另一点F,连结A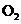 、FG,那么FG·A
、FG,那么FG·A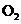 的值是否会发生变化?如果不变,说明理由并求其值;如果变化,求其变化范围。
的值是否会发生变化?如果不变,说明理由并求其值;如果变化,求其变化范围。
1、(2005年贵阳市)在Rt⊿ABC中,∠C =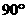 ,AC = 6,BC =
8,点O在CB上,且AO平分∠BAC,CO = 3(如图所示),以点O为圆心,
,AC = 6,BC =
8,点O在CB上,且AO平分∠BAC,CO = 3(如图所示),以点O为圆心, 为半径画圆;
为半径画圆;
(1) 取何值时,⊙O与AB相切;
取何值时,⊙O与AB相切;
(2) 取何值时,⊙O与AB有两个公共点?
取何值时,⊙O与AB有两个公共点?
(3)当⊙O与AB相切时,设切点为D,在BC上是否存在点P,使⊿APD的面积为⊿ABC的面积的一半?若存在,求出CP的长,若不存在,请说明理由;
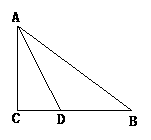
10.(13分)如图2-6-20所示,在 Rt△ABC中,∠ACB=90°,BC的垂直平分线DE,交 BC于 D,交AB于E,F在DE上,并且A F=CE.
⑴ 求证:四边形ACEF是平行四边形;
⑵ 当∠B的大小满足什么条件时,四边形A CEF是菱形?请回答并证明你的结论;
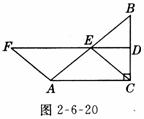 ⑶ 四边形ACEF有可能是正方形吗?为什么?
⑶ 四边形ACEF有可能是正方形吗?为什么?
9.已知二次函数的图象过A(-3,0),B(1,0)两点.
⑴ 当这个二次函数的图象又过点以0,3)时,求其解析式;
⑵ 设⑴中所求 M次函数图象的顶点为P,求SΔAPC:SΔABC的值;
⑶ 如果二次函数图象的顶点M在对称轴上移动,并与y轴交于点D,SΔAMD:SΔABD的值确定吗?为什么?
8.(10分)某校研究性学习小组在研究有关二次函数及其图象性质的问题时,发现了两个重要结论.一是发现抛物线y=ax2+2x+3(a≠0),当实数a变化时,它的顶点都在某条直线上;二是发现当实数a变化时,若把抛物线y=ax2+2x+3(a≠0)的顶点的横坐标减少,纵坐标增加,得到A点的坐标;若把顶点的 横坐标增加,纵坐标增加,得到B点的坐标,则A、B两点一定仍在抛物线y=ax2+2x+3(a≠0)上.
⑴ 请你协助探求出实数a变化时,抛物线y=ax2+2x+3(a≠0)的顶点所在直线的解析式;
⑵ 问题⑴中的直线上有一个点不是该抛物线的顶点,你能找出它来吗?并说明理由;
⑶ 在他们第二个发现的启发下,运用“一般→特殊→一般”的思想,你还能发现什么?你能用数学语言将你的猜想表述出来吗?你的猜想能成立吗?若能成立,请说明理由。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com