
题目列表(包括答案和解析)
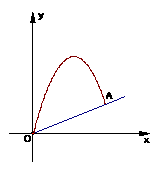 20、今有网球从斜坡
20、今有网球从斜坡 点处抛出,网球的抛物线是
点处抛出,网球的抛物线是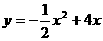 的图象的一段,斜坡的截线
的图象的一段,斜坡的截线 是一次函数
是一次函数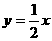 的图象的一段,建立如图所示的直角坐标系;求:⑴、网球抛出的最高点的坐标;
的图象的一段,建立如图所示的直角坐标系;求:⑴、网球抛出的最高点的坐标;
⑵、网球在斜坡的落点 的垂直高度。
的垂直高度。
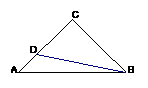
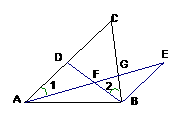 21、已知:如图,
21、已知:如图,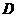 是
是 上一点,
上一点,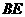 ∥
∥ 、
、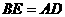 ,
,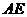 分别交
分别交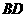 、
、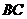 于点
于点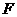 、
、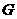 ,
,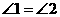 ;
;
⑴、图中哪个三角形与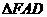 全等?证明你的结论;
全等?证明你的结论;
⑵、探索线段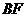 、
、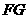 、
、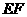 之间的关系,
之间的关系,
并说明理由。
22、如图,在平面直角坐标系中,四边形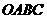 为菱形,点
为菱形,点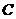 的坐标为
的坐标为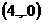 、
、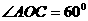 ,垂直于
,垂直于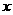 轴的直线
轴的直线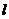 从
从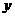 轴出发,沿
轴出发,沿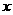 轴正方向以每秒1个单位长度的速度运动,设直线
轴正方向以每秒1个单位长度的速度运动,设直线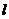 与菱形
与菱形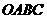 的两边分别交于点
的两边分别交于点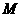 、
、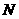 (点
(点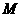 在点
在点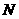 的上方)
的上方)
⑴、求 、
、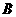 两点坐标;
两点坐标;
⑵、设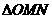 的面积为
的面积为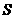 ,直线
,直线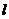 运动时间为
运动时间为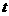 秒
秒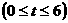 ,试求
,试求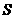 与
与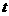 的函数表达式;
的函数表达式;
⑶、在题⑵的条件下,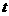 为何值时,
为何值时,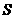 的面积最大?最大面积是多少?
的面积最大?最大面积是多少?
 16、某单位欲从内部聘管理人员一名,对甲、乙、丙三名候选人进行了笔试和面试两项测试,三人的测试成绩如下表所示:
16、某单位欲从内部聘管理人员一名,对甲、乙、丙三名候选人进行了笔试和面试两项测试,三人的测试成绩如下表所示:
|
测试 项目 |
测试成绩/分 |
||
|
甲 |
乙 |
丙 |
|
|
笔试 |
75 |
80 |
90 |
|
面试 |
93 |
70 |
68 |
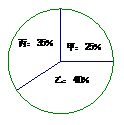
根据录用程序,该单位组织200名职工利用投票推荐的方式对三人进行民主评议,三人的得票率(没有弃权票,每位职工只能推荐1人)如图所示,每得一票记1 分。
⑴、请算出三人的民主评议得分;
⑵、根据上述三项的平均成绩确定录用人选,那么谁将首先被录用?(精确到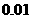 )
)
⑶、根据实际需要,该单位将笔试、面试、民主评议三项按得分4:3:3的比例确定个人成绩,那么谁将被录用。
17、某校共有4个大餐厅和3个小餐厅,经过测试:同时开放1 个大餐厅,2个小餐厅,可供1200人就餐;同时开放2 个大餐厅,1个小餐厅,可供1500人就餐。
⑴、求1个大餐厅, 1个小餐厅分别可供多少名学生就餐;
⑵、若7个餐厅同时开放,能否供全校3500名学生同时就餐?请说明理由。
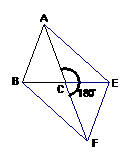 18、已知:如图,在
18、已知:如图,在 中,
中,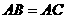 ,若将
,若将 绕点
绕点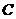 顺时针旋转
顺时针旋转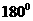 得到
得到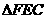 。
。
⑴、试猜想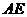 与
与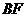 有何关系?给予证明;
有何关系?给予证明;
⑵、若 的面积为
的面积为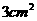 ,
,
求四边形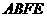 的面积。
的面积。
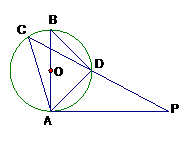 19、如图,
19、如图,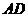 是
是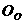 的直径,
的直径,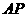 是切线,
是切线, 是切点,
是切点,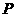 是弦
是弦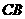 延长线上一点,
延长线上一点,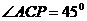
⑴、求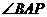 的度数;
的度数;
⑵、若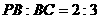 ,且
,且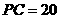 ,求
,求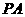 的长。
的长。
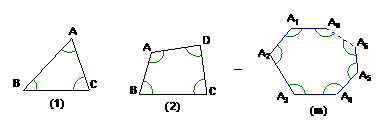
14、如图,①、②、…、⑩是边长均大于2的三角形、四边形、…、凸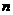 边形,分别以它们的各顶点为圆心,以1为半径画弧与两邻边相交,得到3条弧、4条弧…、
边形,分别以它们的各顶点为圆心,以1为半径画弧与两邻边相交,得到3条弧、4条弧…、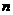 条弧。
条弧。
⑴、图⑴中3条弧的弧长的和为
⑵、图⑵中4条弧的弧长的和为
⑶、求图(m)中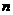 条弧的弧长的和 (用
条弧的弧长的和 (用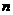 表示)
表示)
 15、已知
15、已知 和
和 的弦
的弦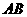
⑴、求作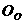 的一个内接
的一个内接 ,使
,使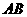 为
为
的一边,且使 与
与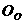 构成轴对称图形;
构成轴对称图形;
⑵、问题⑴中的三角形最多可以作 个。
(保留作图痕迹,不写作法)
13、在等腰直角三角形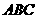 中,
中,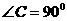 ,
,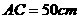 ,
,
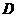 是
是 上一点,若
上一点,若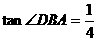 ,求
,求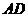 的长。
的长。
12、已知: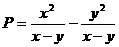 ;
; 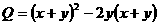 ,小敏、小聪两人在
,小敏、小聪两人在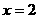 ,
,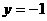 的条件下分别计算了
的条件下分别计算了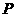 和
和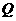 的值,小敏说
的值,小敏说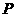 的值比
的值比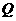 大,小聪说
大,小聪说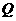 的值比
的值比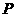 大,请你判断谁的结论正确,并说明理由。
大,请你判断谁的结论正确,并说明理由。
11、已知不等式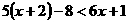 的最小整数解是方程
的最小整数解是方程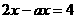 的解,求
的解,求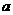 的值。
的值。
10、某公司销售人员的个人月收入与其每月
的销售量成一次函数关系,如图,则此销售
人员的销售量为3千件时的月收入是 元。
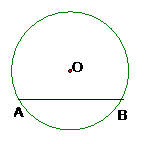
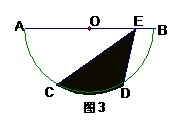
8、如图3,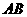 为半圆
为半圆 的直径,
的直径,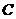 、
、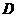 是
是
弧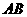 上的三等分点,若
上的三等分点,若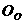 的半径为1,
的半径为1,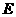 为
为
线段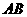 上任意一点,则图中阴影部分的
上任意一点,则图中阴影部分的
面积为
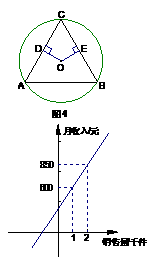 9、如图4,
9、如图4, 是
是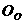 的内接正三角形,
的内接正三角形,
 为圆心,
为圆心,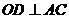 ,
,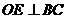 ,
,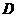 、
、
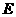 是垂足,若
是垂足,若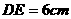 ,则
,则 的面
的面
积是
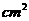
7、反比例函数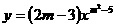 ,当
,当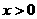 时,
时,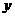 随
随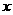 的增大而增大,则
的增大而增大,则 =
=
6、若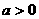 ,
,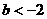 ,则点
,则点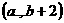 应在第 象限。
应在第 象限。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com