
题目列表(包括答案和解析)
6.解方程: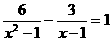
[解]解:6-3(x+1)=x2-1 x2+3x-4=0 x+4)(x-1)=0 x1=-4,x2=1
经检验x=1是增根,应舍去
∴原方程的解为x=-4
5.某商场购进甲、乙两种服装后,都加价40%标价出售。“春节”期间商场搞优惠促销,决定将甲、乙两种服装分别按标价的八折和九折出售。某顾客购买甲、乙两种服装共付款182元,两种服装标价之和为210元,问这两种服装的进价和标价各是多少元?
[解]设甲种服装的标价是x元,则进价是元;乙种服装的标价是y元,则进价是元。
依题意,得:
解之,得:
=50(元),=100(元)
4.解方程组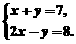
[解]①+②,得 3x=15 ∴ x=15
把x=5代入①,得y=2
∴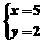 是原方程组的解
是原方程组的解
3.十堰市东方食品厂2003年的利润(总产值-总支出)为200万元,2004年总产值比2003年增加了20%,总支出减少了10%。2004年的利润为780万元。问2003年总产值、总支出各是多少万元?
[解]设2003年的总产值为x万元,则2004年的总产值为(1+20%)x万元,2003年的总支出为y万元,则2004年的总支出为(1-10%)y万元,则有:
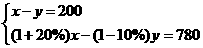
∴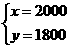
答:2003年的总产值为2000万元,总支出为1800万元
1.已知等式 (2A-7B) x+(3A-8B)=8x+10对一切实数x都成立,求A、B的值.
[解] 由题意有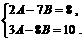 解得:
解得: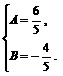
即A、B的值分别为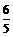 、
、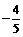 .
.
2为满足市民对优质教育的需求某中学决定改变办学条件计划拆除一部分旧校舍、建造新校舍。拆除旧校舍每平米需80元,建造新校舍每平米需700元。计划在年内拆除旧校舍与建造新校舍共7200平方米,在实施中为扩大绿化面积,新建校舍只完成了计划的80%,而拆除校舍则超过了10%,结果恰好完成了原计划的拆、除的总面积。
(1)求原计划拆建面积各多少平方米?
(2)若绿化1平方米需200元,那么在实际完成的拆、建工程中节余的资金用来绿化大约是多少平方米?
[解]设原计划拆除旧校舍x平方米,新建校舍y平方米,本世纪初题意得:
(1)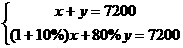 解得
解得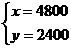
(2)实际比原计划拆除与新建校舍节约资金是
(4800×80-2400×700)-(4800×(1-10%)×80+2400×80%×700)
=297600
用此资金可绿化面积是297600÷200=1488(平方米)
答:原计划拆除旧戌舍4800平方米,新建校舍2400平方米,实际施工中节约的资金可绿化1488平方米
3.为了贫困家庭子女能完成初中学业,国家给他们免费提供教科书,
下表是某中学免费提供教科书补助的部分情况:
|
年级 项目 |
七 |
八 |
九 |
合计 |
|
每人免费补助金额(元) |
109 |
94 |
47.5 |
―― |
|
人数(人) |
|
|
40 |
120 |
|
免费补助总金额(元) |
|
|
1900 |
10095 |
若设获得免费提供教科书补助的七年级为x人,八年级为y人,根据题意列出方程组为( )
A.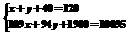 B.
B.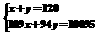 C.
C.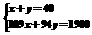 D.
D.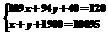
2.某校初三(2)班40名同学为“希望工程”捐款,共捐款100元.捐款情况如下表:
|
捐款(元) |
1 |
|
3 |
4 |
||
|
人 数 |
6 |
|
|
7 |
表格中捐款2元和3元的人数不小心被墨水污染已看不清楚.
若设捐款2元的有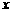 名同学,捐款3元的有
名同学,捐款3元的有 名同学,根据题意,可得方程组
名同学,根据题意,可得方程组
A、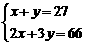 B、
B、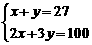 C、
C、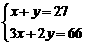 D、
D、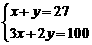
1.方程组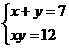 的一个解是( )
的一个解是( )
A.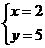 B.
B.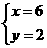 C.
C.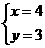 D.
D.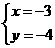
典型例题
9.我市向民族地区的某县赠送一批计算机,首批270台将于近期启运,经与某物资公司联系,得知用A型汽车若干辆刚好装完,用B型汽车不仅可少用1辆,而且有一辆车差30台计算机才装满.
(1)已知B型汽车比A型汽车每辆车可多装15台,求A、B两种型号的汽车各装计算机多少台?
(2)已知A型汽车的运费是每辆350元,B型汽车的运费是每辆400元,若运送这批计算机同时用这两种型号的汽车,其中B型汽车比A型汽车多用1辆,所用运费比单独用任何一种型号的汽车都要节省,按这种方案需A、B两种型号的汽车各多少辆?运费多少元?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com