
题目列表(包括答案和解析)
2. 如图,直线
如图,直线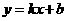 与
与 轴交于点(-4,0),则
轴交于点(-4,0),则 >0时,
>0时, 的取值范围是( )
的取值范围是( )
A、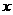 >-4 B、
>-4 B、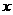 >0
>0
C、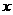 <-4 D、
<-4 D、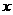 <0
<0
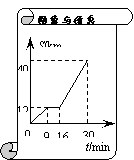
1. 如图是某汽车行驶的路程S(km)与时间t(min) 的函数关系图.观察图中所提供的信息,解答下列问题:
(1)汽车在前9分钟内的平均速度是多少?
(2)汽车在中途停了多长时间?
(3)当16≤t≤30时,求S与t的函数关系式.
9.已知反比例函数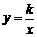 的图象经过点
的图象经过点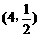 ,若一次函数
,若一次函数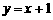 的图象平移后经过该反比例函数图象上的点B(2,m),求平移后的一次函数图象与x轴的交点坐标.
的图象平移后经过该反比例函数图象上的点B(2,m),求平移后的一次函数图象与x轴的交点坐标.
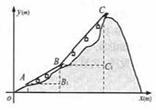 如图,A、B、C表示建筑在一座比较险峻的名山上的三个缆车站的位置,AB、BC表示连接三个缆车站的钢缆。已知A、B、C所处位置的海拔高度分别为124m、400m、1100m,如图建立直角坐标系,即A(a,124)、B(b,400)、C(c,1100),若直线AB的解析式为y=x+4,直线BC与水平线BC1的交角为450。
如图,A、B、C表示建筑在一座比较险峻的名山上的三个缆车站的位置,AB、BC表示连接三个缆车站的钢缆。已知A、B、C所处位置的海拔高度分别为124m、400m、1100m,如图建立直角坐标系,即A(a,124)、B(b,400)、C(c,1100),若直线AB的解析式为y=x+4,直线BC与水平线BC1的交角为450。
⑴分别求出A、B、C三个缆车站所在位置的坐标;
 [课后作业]
[课后作业]
(13)一次函数
8.某地电话拨号入网有两种收费方式,用户可以任选其一:
 (A)计时制:0.05元/分;(B)包月制:50元/月(限一部个人住宅电话上网).
(A)计时制:0.05元/分;(B)包月制:50元/月(限一部个人住宅电话上网).
此外,每一种上网方式都得加收通信费0.02元/分.
(1) (4分)请你分别写出两种收费方式下用户每月应支付的费用y(元)与上网时间x(小时)之间的函数关系式;
(2) (1分) 若某用户估计一个月内上网的时间为20小时,你认为采用哪种方式较为合算?
7.(1) 甲品牌拖拉机开始工作时,油箱中有油30升.如果每小时耗油6升,求油箱中的余油量y(升)与工作时间x(时)之间的函数关系式.
 (2) 如图,线段AB表示乙品牌拖拉机在工作时油箱中的余油量y(升)与工作时间x(时)之间的函数关系的图象. 若甲、乙两种品牌的拖拉机在售价、质量、性能、售后服务等条件上都一样.根据图象提供的信息,你愿意购买哪种品牌的拖拉机,并说明理由.
(2) 如图,线段AB表示乙品牌拖拉机在工作时油箱中的余油量y(升)与工作时间x(时)之间的函数关系的图象. 若甲、乙两种品牌的拖拉机在售价、质量、性能、售后服务等条件上都一样.根据图象提供的信息,你愿意购买哪种品牌的拖拉机,并说明理由.
6.某产品每件成本10元,试销阶段每件产品的日销售价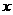 (元)与产品的日销售量
(元)与产品的日销售量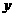 (件)之间的关系如下表:
(件)之间的关系如下表:
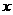 (元) (元) |
15 |
20 |
25 |
30 |
… |
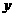 (件) (件) |
25 |
20 |
15 |
10 |
… |
(1)在草稿纸上描点,观察点的颁布,建立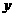 与
与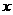 的恰当函数模型。
的恰当函数模型。
(2)要使每日的销售利润最大,每件产品的销售价应定为多少元?此时每日销售利润是多少元?
5.如图,某种旅行帽的帽沿接有两个塑料帽带,其中一个塑料帽带上有7个等距的小圆柱体扣,另一个帽带上扎有七个等距的扣眼,下表列出的是用第一扣分别去扣不同扣眼所测得帽圈直径的有关数据(单位:cm);
|
扣眼号数(x) |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
帽圈直径(y) |
22.92 |
22.60 |
22.28 |
21.96 |
21.64 |
21.32 |
21.00 |
⑴求帽圈直径y与扣眼号数x之间的一次函数关系式;
⑵小强的头围约为68.94cm,他将第一扣扣到第4号扣眼,你认为松紧合适吗?
4.某纺织厂生产的产品,原来每件出厂价为80元,成本为60元.由于在生产过程中平均每生产一件产品有0.5米3的污水排出,现在为了保护环境,需对污水净化处理后再排出.已知每处理1米3污水的费用为2元,且每月排污设备损耗为8000元.设现在该厂每月生产产品x件,每月纯利润y元:
①求出y与x的函数关系式.(纯利润=总收入-总支出)
 ②当y=106000时,求该厂在这个月中生产产品的件数.
②当y=106000时,求该厂在这个月中生产产品的件数.
3.老师给出一个函数,甲、乙、丙各正确指出了这个函数的一个性质:甲:函数的图象经过第一象限;乙:函数的图象经过第三象限;丙:在每个象限内,y随x的增大而减小.
请你根据他们的叙述构造满足上述性质的一个函数: .
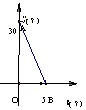
2.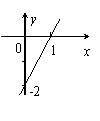 已知一次函数y=kx+b的图象如图,当x<0时,y的取值范围是( )
已知一次函数y=kx+b的图象如图,当x<0时,y的取值范围是( )
A、y>0 B、y<0
C、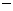 2<y<0 D、y<
2<y<0 D、y<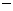 2
2
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com