
题目列表(包括答案和解析)
10. 在平面直角坐标系中,已知A(0,2),B(4,0),设P、Q分别是线段AB、OB上的动点,它们同时出发,点P以每秒3个单位的速度从点A向点B运动,点Q以每秒1个单位的速度从点B向点O运动.设运动时间为t(秒).
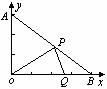 (1)用含t的代数式表示点P的坐标;
(1)用含t的代数式表示点P的坐标;
(2)当t为何值时,△OPQ为直角三角形?
(3)在什么条件下,以Rt△OPQ的三个顶点能确定一条对称轴平行于y轴的抛物线?选择一种情况,求出所确定的抛物线的解析式.
解:(1)作PM⊥y轴,PN⊥x轴.∵OA=3,OB=4,∴AB=5.
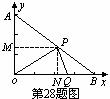 ∵PM∥x轴,∴
∵PM∥x轴,∴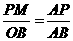 .∴
.∴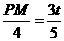 .∴PM=
.∴PM=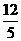 t.
t.
∵PN∥y轴,∴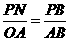 .∴
.∴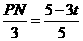 .∴PN=3-
.∴PN=3-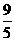 t.
t.
∴点P的坐标为(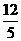 t,3-
t,3-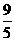 t).
t).
(2)①当∠POQ=90°时,t=0,△OPQ就是△OAB,为直角三角形.
②当∠OPQ=90°时,△OPN∽△PQN,∴PN2=ON•NQ.(3-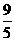 t)2=
t)2=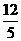 t(4-t-
t(4-t-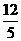 t).
t).
化简,得19t2-34t+15=0.解得t=1或t=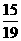 .
.
③当∠OQP=90°时,N、Q重合.∴4-t=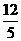 t,∴t=
t,∴t=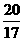 .
.
综上所述,当t=0,t=1,t=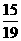 ,t=
,t=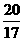 时,△OPQ为直角三角形.
时,△OPQ为直角三角形.
(3)当t=1或t=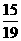 时,即∠OPQ=90°时,以Rt△OPQ的三个顶点可以确定一条对称轴平行于y轴的抛物线.当t=1时,点P、Q、O三点的坐标分别为P(
时,即∠OPQ=90°时,以Rt△OPQ的三个顶点可以确定一条对称轴平行于y轴的抛物线.当t=1时,点P、Q、O三点的坐标分别为P(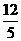 ,
,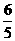 ),Q(3,0),O(0,0).设抛物线的解析式为y=a(x-3)(x-0),即y=a(x2-3x).将P(
),Q(3,0),O(0,0).设抛物线的解析式为y=a(x-3)(x-0),即y=a(x2-3x).将P(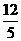 ,
,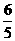 )代入上式,得a=-
)代入上式,得a=-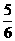 .∴y=-
.∴y=-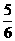 (x2-3x).
(x2-3x).
即y=-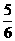 x2+
x2+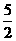 x.
x.
说明:若选择t=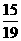 时,点P、Q、O三点的坐标分别是P(
时,点P、Q、O三点的坐标分别是P(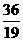 ,
,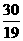 ),Q(
),Q(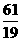 ,0),O(0,0).求得抛物线的解析式为y=-
,0),O(0,0).求得抛物线的解析式为y=-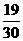 x2+
x2+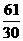 x,相应给分.
x,相应给分.
9. 如图,在平面直角坐标系中,点A、B分别在x轴、y轴上,线段OA、OB的长(0A<OB)是方程x2-18x+72=0的两个根,点C是线段AB的中点,点D在线段OC上,OD=2CD.
(1)求点C的坐标;
(2)求直线AD的解析式;
(3)P是直线AD上的点,在平面内是否存在点Q,使以0、A、P、Q为顶点的四边形是菱形?若存在,请直接写出点Q的坐标;若不存在,请说明理由.
解:(1)OA=6,OB=12 ,
点C是线段AB的中点,OC=AC.
作CE⊥x轴于点E.
∴ OE=OA=3,CE=OB=6.
∴ 点C的坐标为(3,6).
(2)作DF⊥x轴于点F
△OFD∽△OEC,=,于是可求得OF=2,DF=4.
∴ 点D的坐标为(2,4).
设直线AD的解析式为y=kx+b.
把A(6,0),D(2,4)代人得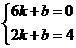 ,
,
解得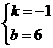 ,
,
∴ 直线AD的解析式为y=-x+6 .
(3)存在.
Q1(-3,3);
Q2(3,-3);
Q3(3,-3) ;
Q4(6,6) .
8.已知一次函数y=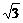 +m(O<m≤1)的图象为直线
+m(O<m≤1)的图象为直线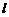 ,直线
,直线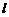 绕原点O旋转180°后得直线
绕原点O旋转180°后得直线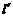 ,△ABC三个顶点的坐标分别为A(-
,△ABC三个顶点的坐标分别为A(-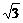 ,-1)、B(
,-1)、B(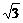 ,-1)、C(O,2).
,-1)、C(O,2).
(1)直线AC的解析式为________,直线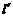 的解析式为________ (可以含m);
的解析式为________ (可以含m);
(2)如图,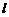 、
、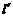 分别与△ABC的两边交于E、F、G、H,当m在其范围内变化时,判断四边形EFGH中有哪些量不随m的变化而变化?并简要说明理由;
分别与△ABC的两边交于E、F、G、H,当m在其范围内变化时,判断四边形EFGH中有哪些量不随m的变化而变化?并简要说明理由;
(3)将(2)中四边形EFGH的面积记为S,试求m与S的关系式,并求S的变化范围;
(4)若m=1,当△ABC分别沿直线y=x与y=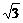 x平移时,判断△ABC介于直线
x平移时,判断△ABC介于直线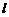 ,
,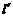 之间部分的面积是否改变?若不变请指出来.若改变请写出面积变化的范围.(不必说明理由)
之间部分的面积是否改变?若不变请指出来.若改变请写出面积变化的范围.(不必说明理由)
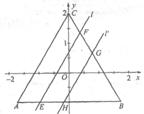
解: (1)y=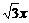 +2 y=
+2 y=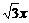 -m
-m
(2)不变的量有:
①四边形四个内角度数不变, 理由略;
②梯形EFGH中位线长度不变(或EF+GH不变),理由略.
(3)S=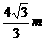 0<m≤1 0<s≤
0<m≤1 0<s≤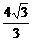
(4)沿y=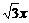 平移时,面积不变;沿y=x平移时,面积改变,设其面积为
平移时,面积不变;沿y=x平移时,面积改变,设其面积为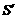 ,则
,则
0<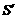 ≤
≤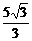
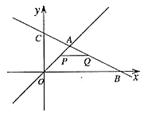
7.如图,在平面直角坐标系中,两个函数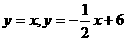 的图象交于点A。动点P从点O开始沿OA方向以每秒1个单位的速度运动,作PQ∥x轴交直线BC于点Q,以PQ为一边向下作正方形PQMN,设它与△OAB重叠部分的面积为S.
的图象交于点A。动点P从点O开始沿OA方向以每秒1个单位的速度运动,作PQ∥x轴交直线BC于点Q,以PQ为一边向下作正方形PQMN,设它与△OAB重叠部分的面积为S.
(1)求点A的坐标.
(2)试求出点P在线段OA上运动时,S与运动时间t(秒)的关系式.
(3)在(2)的条件下,S是否有最大值?若有,求出t为何值时,S有最大值,并求出最大值;若没有,请说明理由.
(4)若点P经过点A后继续按原方向、原速度运动,当正方形PQMN与△OAB重叠部分面积最大时,运动时间t满足的条件是____________.
 解:(1)由
解:(1)由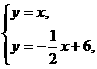 可得
可得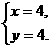
∴A(4,4)。
(2)点P在y = x上,OP = t,
则点P坐标为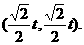
点Q的纵坐标为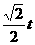 ,并且点Q在
,并且点Q在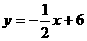 上。
上。
∴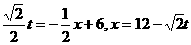 ,
,
即点Q坐标为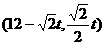 。
。
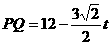 。
。
当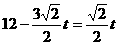 时,
时,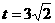 。
。
当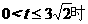 ,
,
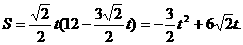
当点P到达A点时,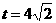 ,
,
当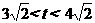 时,
时,
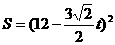
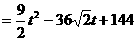 。
。
(3)有最大值,最大值应在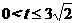 中,
中,
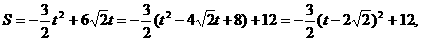
当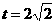 时,S的最大值为12.
时,S的最大值为12.
(4)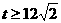 .
.
6.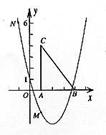 如图,二资助函数
如图,二资助函数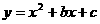 的图象经过点M(1,-2)、N(-1,6).
的图象经过点M(1,-2)、N(-1,6).
(1)求二次函数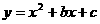 的关系式.
的关系式.
(2)把Rt△ABC放在坐标系内,其中∠CAB = 90°,点A、B的坐标分别为(1,0)、(4,0),BC = 5。将△ABC沿x轴向右平移,当点C落在抛物线上时,求△ABC平移的距离.
解:(1)∵M(1,-2),N(-1,6)在二次函数y = x2+bx+c的图象上,
∴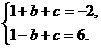 解得
解得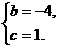
二次函数的关系式为y = x2-4x+1.
(2)Rt△ABC中,AB = 3,BC = 5,∴AC = 4,
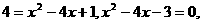
解得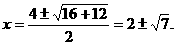
∵A(1,0),∴点C落在抛物线上时,△ABC向右平移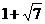 个单位.
个单位.
5.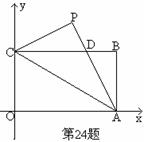 已知如图,矩形OABC的长OA=
已知如图,矩形OABC的长OA=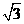 ,宽OC=1,将△AOC沿AC翻折得△APC。
,宽OC=1,将△AOC沿AC翻折得△APC。
(1)填空:∠PCB=____度,P点坐标为( , );
(2)若P,A两点在抛物线y=-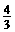 x2+bx+c上,求b,c的值,并说明点C在此抛物线上;
x2+bx+c上,求b,c的值,并说明点C在此抛物线上;
(3)在(2)中的抛物线CP段(不包括C,P点)上,是否存在一点M,使得四边形MCAP的面积最大?若存在,求出这个最大值及此时M点的坐标;若不存在,请说明理由.
(1)30,(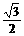 ,
,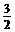 );
);
(2)∵点P(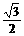 ,
,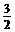 ),A(
),A(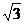 ,0)在抛物线上,故 -
,0)在抛物线上,故 -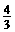 ×
×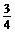 +b×
+b×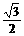 +c=
+c=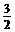 ,-
,-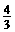 ×3+b×
×3+b×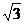 +c=0, ∴b=
+c=0, ∴b=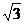 ,c=1. ∴抛物线的解析式为y=-
,c=1. ∴抛物线的解析式为y=-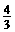 x2+
x2+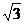 x+1,C点坐标为(0,1). ∵-
x+1,C点坐标为(0,1). ∵-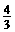 ×02+
×02+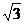 ×0+1=1,
×0+1=1,
∴ 点C在此抛物上.

4.已知函数y=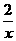 和y=kx+l(k≠O).
和y=kx+l(k≠O).
(1)若这两个函数的图象都经过点(1,a),求a和k的值;
(2)当k取何值时,这两个函数的图象总有公共点?
解;(1)
∵两函数的图象都经过点(1,a),∴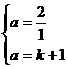 ∴
∴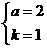
(2)将y=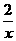
 代人y=kx+l,消去y.得kx2+x一2=0.
代人y=kx+l,消去y.得kx2+x一2=0.
∵k≠O,∴要使得两函数的图象总有公共点,只要△≥0即可.
∵△=1+8k,
∴1+8k≥0,解得k≥一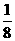
∴k≥一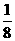 且k≠0.
且k≠0.
3.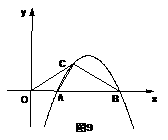 如图9,抛物线y=ax2+8ax+12a与
如图9,抛物线y=ax2+8ax+12a与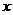 轴交于A、B两点(点A在点B的左侧),抛物线上另有一点
轴交于A、B两点(点A在点B的左侧),抛物线上另有一点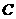 在第一象限,满足∠ ACB为直角,且恰使△OCA∽△OBC.
在第一象限,满足∠ ACB为直角,且恰使△OCA∽△OBC.
(1) 求线段OC的长.
(2) 求该抛物线的函数关系式.
(3) 在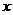 轴上是否存在点P,使△BCP为等腰三角形?
轴上是否存在点P,使△BCP为等腰三角形?
若存在,求出所有符合条件的P点的坐标;若不存在,
请说明理由.
解:(1)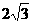 ;(2)
;(2)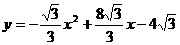 ;(3)4个点:
;(3)4个点:
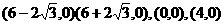
2.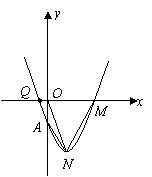 已知抛物线
已知抛物线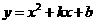 经过点
经过点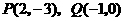 .
.
(1)求抛物线的解析式.
(2)设抛物线顶点为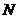 ,与
,与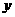 轴交点为
轴交点为 .求
.求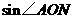 的值.
的值.
(3)设抛物线与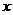 轴的另一个交点为
轴的另一个交点为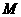 ,求四边形
,求四边形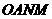 的面积.
的面积.
解:(1)解方程组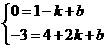
得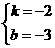 ,
,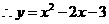 .
.
(2)顶点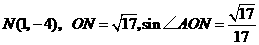 .
.
(3)在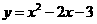 中,令
中,令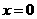 得
得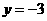 ,
,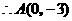 ,
,
令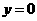 得
得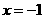 或
或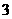 ,
,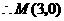 .
.
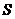 四边形
四边形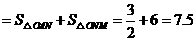 (面积单位)
(面积单位)
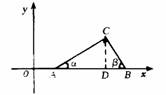
1. 如图,已知点A(tanα,0),B(tanβ,0)在x轴正半轴上,点A在点B的左边,α、β 是以线段AB为 斜边、顶点C在x轴上方的Rt△ABC的两个锐角.
(1)若二次函数y=-x2-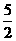 kx+(2+2k-k2)的图象经过A、B两点,求它的解析式;
kx+(2+2k-k2)的图象经过A、B两点,求它的解析式;
(2)点C在(1)中求出的二次函数的图象上吗?请说明理由.
解:(1)∵ α,β是Rt△ABC的两个锐角,
∴ tanα·tanβ=1.tanα>0,tanβ>0.
由题知tanα,tanβ是方程
x2+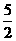 kx-(2+2k-k2)=0的两个根,
kx-(2+2k-k2)=0的两个根,
∴ tanx·tanβ=(2=2k-k2)=k2-2k-2,∴ k2-2k-2=1.
解得,k=3或k=-1.
而tanα+tanβ=-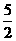 k>0,
k>0,
∴ k<0.∴ k=3应舍去,k=-1.
故所求二次函数的解析式为y=-x2+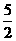 x-1.
x-1.
(2)不在.
过C作CD⊥AB于D.
令y=0,得-x2+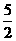 x-1=0,
x-1=0,
解得x1=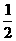 ,x2=2.
,x2=2.
∴ A(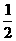 ,0),B(2,0),AB=
,0),B(2,0),AB=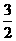 .
.
∴ tanα=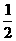 ,tanβ=2.设CD=m.则有CD=AD·tanα=
,tanβ=2.设CD=m.则有CD=AD·tanα=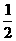 AD.
AD.
∴ AD=2CD.
又CD=BD·tanβ=2BD,
∴ BD=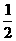 CD.
CD.
∴ 2m+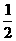 m=
m=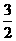 .
.
∴ m=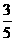 .∴ AD=
.∴ AD=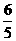 .
.
∴ C(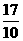 ,
,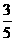 ).
).
当x=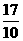 时,y=
时,y=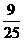 ≠
≠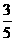
∴ 点C不在(1)中求出的二次函数的图象上.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com