
题目列表(包括答案和解析)
30.已知关于x的二次函数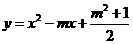 与
与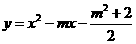 ,这两个二次函数的图象中的一条与x轴交于A, B两个不同的点.
,这两个二次函数的图象中的一条与x轴交于A, B两个不同的点.
(l)试判断哪个二次函数的图象经过A, B两点;
(2)若A点坐标为(-1, 0),试求B点坐标;
(3)在(2)的条件下,对于经过A, B两点的二次函数,当x取何值时,y的值随x值的增大而减小?
解:(l)对于关于x的二次函数y =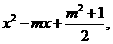
由于△=(-m )
2-4×l×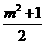 =-m2-2<0,
=-m2-2<0,
所以此函数的图象与x轴没有交点
对于关于x的二次函数 y =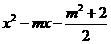 .
.
由于△=(-m ) 2-4
×l×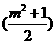 =-m2-2<0,
=-m2-2<0,
所以此函数的图象与x轴没有交点
对于关于x的二次函数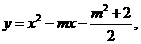
由于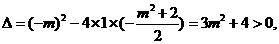
所以此函数的图象与x轴有两个不同的交点.
故图象经过A、B两点的二次函数为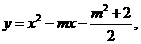
(2 )将A(-1,0)代入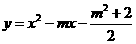 ,得
,得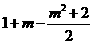 =0.
=0.
整理,得m2-2m = 0 .
解之,得m=0,或m = 2.
当m =0时,y=x2-1.令y = 0,得x2-1 = 0.
解这个方程,得x1=-1,x2=1
此时,B点的坐标是B (l, 0).
当m=2时,y=x2-2x-3.令y=0,得x2-2x-3=0.
解这个方程,得x1=-1,x2=3
此时,B点的坐标是B(3,0).
(3) 当m =0时,二次函数为y=x2-1,此函数的图象开口向上,对称轴为x=0,所以当x<0时,函数值 y 随:的增大而减小.
当m=2时,二次函数为y = x2-2 x-3 = (x-1)2-4, 此函数的图象开口向上,对称轴为x = l,所以当x < l 时,函数值y随x的增大而减小.
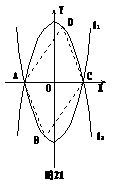
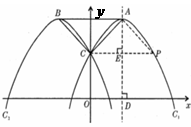
29、 如图,已知抛物线L1: y=x2-4的图像与x有交于A、C两点,
(1)若抛物线l2与l1关于x轴对称,求l2的解析式;
(2)若点B是抛物线l1上的一动点(B不与A、C重合),以AC为对角线,A、B、C三点为顶点的平行四边形的第四个顶点定为D,求证:点D在l2上;
(3)探索:当点B分别位于l1在x轴上、下两部分的图像上时,平行四边形ABCD的面积是否存在最大值和最小值?若存在,判断它是何种特殊平行四边形,并求出它的面积;若不存在,请说明理由.
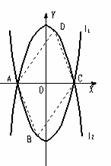
解:设l2的解析式为y=a(x-h)2+k
∵l2与x轴的交点A(-2,0),C(2,0),顶点坐标是(0,-4),l1与l2关于x轴对称,
∴l2过A(-2,0),C(2,0),顶点坐标是(0,4)
∴y=ax2+4
∴0=4a+4 得 a=-1
∴l2的解析式为y=-x2+4
(2)设B(x1 ,y1)
∵点B在l1上
∴B(x1 ,x12-4)
∵四边形ABCD是平行四边形,A、C关于O对称
∴B、D关于O对称
∴D(-x1 ,-x12+4).
将D(-x1 ,-x12+4)的坐标代入l2:y=-x2+4
∴左边=右边
∴点D在l2上.
(3)设平行四边形ABCD的面积为S,则
S=2*S△ABC =AC*|y1|=4|y1|
a.当点B在x轴上方时,y1>0
∴S=4y1 ,它是关于y1的正比例函数且S随y1的增大而增大,
∴S既无最大值也无最小值
b.当点B在x轴下方时,-4≤y1<0
∴S=-4y1 ,它是关于y1的正比例函数且S随y1的增大而减小,
∴当y1 =-4时,S由最大值16,但他没有最小值
此时B(0,-4)在y轴上,它的对称点D也在y轴上.9分
∴AC⊥BD
∴平行四边形ABCD是菱形
此时S最大=16.
28. 如图10(单位:m),等腰三角形ABC以2米/秒的速度沿直线L向正方形移动,直到AB与CD重合。设x秒时,三角形与正方形重叠部分的面积为y
如图10(单位:m),等腰三角形ABC以2米/秒的速度沿直线L向正方形移动,直到AB与CD重合。设x秒时,三角形与正方形重叠部分的面积为y .
.
(1)写出y与x的关系式;
(2)当x=2,3.5时,y分别是多少?
(3)当重叠部分的面积是正方形面积的一半时,
三角形移动了多长时间?
(1)y=2x2
(2)8;24.5
(3)5秒
27.已知抛物线 :
: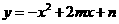 (
( ,
,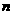 为常数,且
为常数,且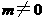 ,
,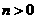 )的顶点为
)的顶点为 ,与
,与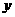 轴交于点
轴交于点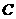 ;抛物线
;抛物线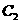 与抛物线
与抛物线 关于
关于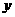 轴对称,其顶点为
轴对称,其顶点为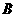 ,连接
,连接 ,
,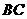 ,
,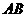 .
.
注:抛物线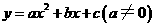 的顶点坐标为
的顶点坐标为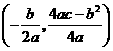 .
.
(1)请在横线上直接写出抛物线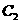 的解析式:________________________;
的解析式:________________________;
(2)当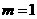 时,判定
时,判定 的形状,并说明理由;
的形状,并说明理由;
(3)抛物线 上是否存在点
上是否存在点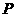 ,使得四边形
,使得四边形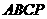 为菱形?如果存在,请求出
为菱形?如果存在,请求出 的值;如果不存在,请说明理由.
的值;如果不存在,请说明理由.
解:(1)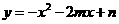 .
.
(2)当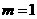 时,
时, 为等腰直角三角形.
为等腰直角三角形.
理由如下:
如图: 点
点 与点
与点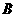 关于
关于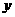 轴对称,点
轴对称,点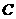 又在
又在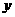 轴上,
轴上,
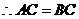 .
.
过点 作抛物线
作抛物线 的对称轴交
的对称轴交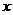 轴于
轴于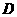 ,过点
,过点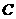 作
作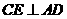 于
于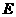 .
.
 当
当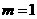 时,顶点
时,顶点 的坐标为
的坐标为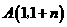 ,
,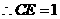 .
.
又 点
点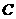 的坐标为
的坐标为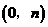 ,
,
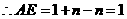 .
.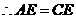 .
.
从而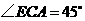 ,
,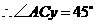 .
.
由对称性知 ,
,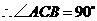 .
.
 为等腰直角三角形.
为等腰直角三角形.
(3)假设抛物线 上存在点
上存在点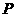 ,使得四边形
,使得四边形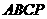 为菱形,则
为菱形,则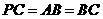 .
.
由(2)知,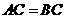 ,
,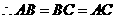 .
.
从而 为等边三角形.
为等边三角形.
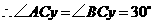 .
.
 四边形
四边形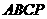 为菱形,且点
为菱形,且点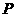 在
在 上,
上, 点
点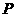 与点
与点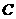 关于
关于 对称.
对称.
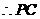 与
与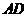 的交点也为点
的交点也为点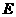 ,因此
,因此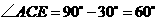 .
.
 点
点 的坐标分别为
的坐标分别为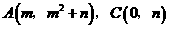 ,
,
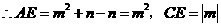 .
.
在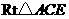 中,
中,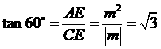 .
.
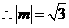 ,
,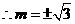 .
.
故抛物线 上存在点
上存在点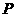 ,使得四边形
,使得四边形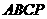 为菱形,此时
为菱形,此时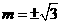 .
.
26.如图,已知抛物线与x轴交于A(m,0)、B(n,0)两点,与y轴交于点C(0, 3),点P是抛物线的顶点,若m-n= -2,m·n =3.
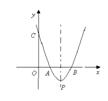 (1)求抛物线的表达式及P点的坐标;
(1)求抛物线的表达式及P点的坐标;
(2)求△ACP的面积S△ACP.
解: (1)设抛物线的表达式为y=ax2+bx+c,∵抛物线过C(0,3),∴c=3,
 又∵抛物线与x轴交于A(m,0)、B(n,0)两点,
又∵抛物线与x轴交于A(m,0)、B(n,0)两点,
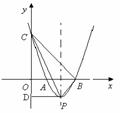
∴m、n为一元二次方程ax2+bx+3=0的解,
∴m+n=-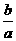 ,mn=
,mn=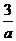 ,
,
由已知m-n= -2,m·n =3,∴解之得a=1,b=-4;m=1,n=3,
∴ 抛物线的表达式为y=x2-4x+3,P点的坐标是(2,1)
(2)由(1)知,抛物线的顶点P(2,-1),过P作PD垂直于y轴于点D,所以,S△BCP =S梯形CBPD-S△CPD=S△COB+ S梯形OBPD- S△CPD,
∵B(3,0),C(0,3),
∴S△BCP
=S△COB+ S梯形OBPD- S△CPD=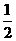 ×3×3+
×3×3+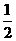 ×1×(3+2)-
×1×(3+2)-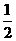 ×2×4=3.
×2×4=3.
25. 已知:如图,A(0,1)是y轴上一定点,B是x轴上一动点,以AB为边,在∠OAB的外部作∠BAE=∠OAB ,过B作BC⊥AB,交AE于点C.
(1)当B点的横坐标为时,求线段AC的长;
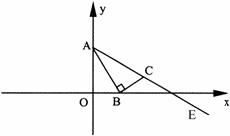 (2)当点B在x轴上运动时,设点C的纵、横坐标分别为y、x,试求y与x的函数关系式(当点B运动到O点时,点C也与O点重合);
(2)当点B在x轴上运动时,设点C的纵、横坐标分别为y、x,试求y与x的函数关系式(当点B运动到O点时,点C也与O点重合);
(3)设过点P(0,-1)的直线l与(2)中所求函数的图象有两个公共点M1(x1,y1)、M2(x2,y2),且x12+x22-6(x1+x2)=8,求直线l的解析式.
解:(1)方法一:在Rt△AOB中,可求得AB=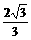
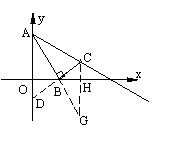 ∵∠OAB=∠BAC,∠AOB=∠ABC=Rt∠ ,∴△ABO∽△ABC ,∴
∵∠OAB=∠BAC,∠AOB=∠ABC=Rt∠ ,∴△ABO∽△ABC ,∴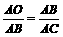 ,由此可求得:AC=
,由此可求得:AC=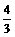
方法二:由题意知:tan∠OAB=

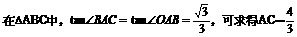
(2)方法一:当B不与O重合时,延长CB交y轴于点D,过C作CH⊥x轴,交x轴于点H,则可证得AC=AD,BD=--4′
∵AO⊥OB,AB⊥BD,∴△ABO∽△BDO,则OB2=AO×OD----6′,即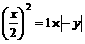
化简得:y=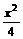 ,当O、B、C三点重合时,y=x=0,∴y与x的函数关系式为:y=
,当O、B、C三点重合时,y=x=0,∴y与x的函数关系式为:y=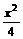
方法二:过点C作CG⊥x轴,交AB的延长线于点H,则AC2=(1-y)2+x2=(1+y)2,化简即可得。
(3)设直线的解析式为y=kx+b,则由题意可得: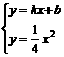 ,消去y得:x2-4kx-4b=0,则有
,消去y得:x2-4kx-4b=0,则有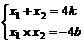 ,由题设知:
,由题设知:
x12+x22-6(x1+x2)=8,即(4k)2+8b-24k=8,且b=-1,则16k2-24k -16=0,解之得:k1=2,k2=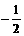 ,当k1=2、b=-1时,
,当k1=2、b=-1时,
△=16k2+16b=64-16>0,符合题意;当k2=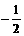 ,b=-1时,△=16k2+16b=4-16<0,不合题意(舍去),∴所求的直线l的解析式为:y=2x-1
,b=-1时,△=16k2+16b=4-16<0,不合题意(舍去),∴所求的直线l的解析式为:y=2x-1
24. 已知:抛物线y=-x2+4x-3与x轴相交于A、B两点(A点在B点的左侧),顶点为P.
(1)求A、B、P三点坐标;
(2) 在下面的直角坐标系内画出此抛物线的简图,并根据简图写出当x取何值时,函数值y大于零;
(3)确定此抛物线与直线y=-2x+6公共点的个数,并说明理由.
解:(1)求得A(1,0),B (3,0), P (2,1)
(2)作图正确 当1<x<3时,y>0
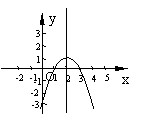 (3)由题意列方程组得:
(3)由题意列方程组得: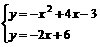
转化得:x2-6x+9=0
△ =0,∴方程的两根相等,
方程组只有一组解
∴此抛物线与直线有唯一的公共点
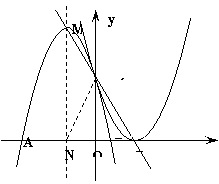
23. 已知抛物线
已知抛物线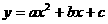 与y
与y
轴的交点为C,顶点为M,直线CM的解析式 y=-x+2
并且线段CM的长为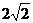
(1) 求抛物线的解析式。
(2) 设抛物线与x轴有两个交点A(X1 ,0)、B(X2 ,0),
且点A在B的左侧,求线段AB的长。
(3) 若以AB为直径作⊙N,请你判断直线CM与⊙N的位置关系,并说明理由。
(1)解法一:由已知,直线CM:y=-x+2与y轴交于点C(0,2)抛物线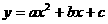 过点C(0,2),所以c=2,抛物线
过点C(0,2),所以c=2,抛物线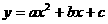 的顶点M
的顶点M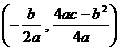 在直线CM上,所以
在直线CM上,所以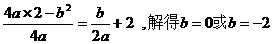
若b=0,点C、M重合,不合题意,舍去,所以b=-2。即M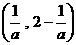
过M点作y轴的垂线,垂足为Q,在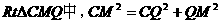
所以,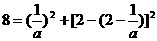 ,解得,
,解得,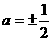 。
。
∴所求抛物线为: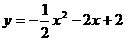 或
或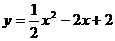 以下同下。
以下同下。
(1)解法二:由题意得C(0 , 2),设点M的坐标为M(x ,y)
∵点M在直线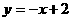 上,∴
上,∴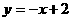
由勾股定理得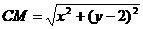 ,∵
,∵
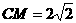
∴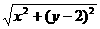 =
=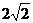 ,即
,即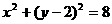
解方程组 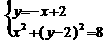 得
得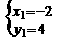
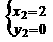
∴M(-2,4) 或 M‘ (2,0)
当M(-2,4)时,设抛物线解析式为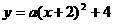 ,∵抛物线过(0,2)点,
,∵抛物线过(0,2)点,
∴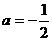 ,∴
,∴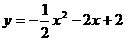
当M‘(2,0)时,设抛物线解析式为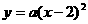
∵抛物线过(0,2)点,∴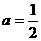 ,∴
,∴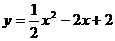
 ∴所求抛物线为:
∴所求抛物线为: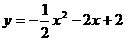 或
或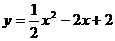
(2)∵抛物线与x轴有两个交点,
∴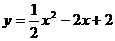 不合题意,舍去。
不合题意,舍去。
∴抛物线应为: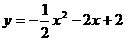
抛物线与x轴有两个交点且点A在B的左侧,∴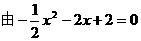 ,得
,得
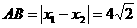
(3)∵AB是⊙N的直径,∴r =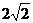 , N(-2,0),又∵M(-2,4),∴MN = 4
, N(-2,0),又∵M(-2,4),∴MN = 4
设直线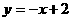 与x轴交于点D,则D(2,0),∴DN = 4,可得MN = DN,∴
与x轴交于点D,则D(2,0),∴DN = 4,可得MN = DN,∴
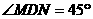 ,作NG⊥CM于G,在
,作NG⊥CM于G,在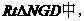
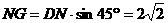 = r
= r
即圆心到直线CM的距离等于⊙N的半径,∴直线CM与⊙N相切
22.已知抛物线y=ax2+bx+c经过点(1,2).
(1)若a=1,抛物线顶点为A,它与x轴交于两点B、C,且△ABC为等边三角形,求b的值.
(2)若abc=4,且a≥b≥c,求|a|+|b|+|c|的最小值.
解:⑴由题意,a+b+c=2, ∵a=1,∴b+c=1
抛物线顶点为A(-,c-)
设B(x1,0),C(x2,0),∵x1+x2=-b,x1x2=c,△=b2-4c>0
∴|BC|=| x1-x2|===
∵△ABC为等边三角形,∴ -c=
即b2-4c=2·,∵b2-4c>0,∴=2
∵c=1-b, ∴b2+4b-16=0, b=-2±2
所求b值为-2±2
⑵∵a≥b≥c,若a<0,则b<0,c<0,a+b+c<0,与a+b+c=2矛盾.
∴a>0.
∵b+c=2-a,bc=
∴b、c是一元二次方程x2-(2-a)x+=0的两实根.
∴△=(2-a)2-4×≥0,
∴a3-4a2+4a-16≥0, 即(a2+4)(a-4)≥0,故a≥4.
∵abc>0,∴a、b、c为全大于0或一正二负.
①若a、b、c均大于0,∵a≥4,与a+b+c=2矛盾;
②若a、b、c为一正二负,则a>0,b<0,c<0,
则|a|+|b|+|c|=a-b-c=a-(2-a)=2a-2,
∵ a≥4,故2a-2≥6
当a=4,b=c=-1时,满足题设条件且使不等式等号成立.
故|a|+|b|+|c|的最小值为6.
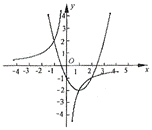
21. (2006·北京市海淀区)已知抛物线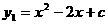 的部分图象如图1所示。
的部分图象如图1所示。
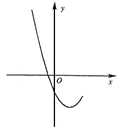
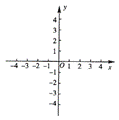
图1 图2
(1)求c的取值范围;
(2)若抛物线经过点(0,-1),试确定抛物线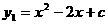 的解析式;
的解析式;
(3)若反比例函数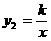 的图象经过(2)中抛物线上点(1,a),试在图2所示直角坐标系中,画出该反比例函数及(2)中抛物线的图象,并利用图象比较
的图象经过(2)中抛物线上点(1,a),试在图2所示直角坐标系中,画出该反比例函数及(2)中抛物线的图象,并利用图象比较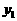 与
与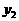 的大小.22. 解:(1)根据图象可知
的大小.22. 解:(1)根据图象可知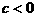
且抛物线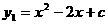 与x轴有两个交点
与x轴有两个交点
所以一元二次方程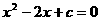 有两个不等的实数根。
有两个不等的实数根。
所以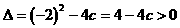 ,且
,且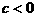
所以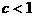
(2)因为抛物线经过点(0,-1)
把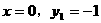 代入
代入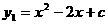
得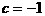
故所求抛物线的解析式为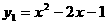
(3)因为反比例函数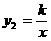 的图象经过抛物线
的图象经过抛物线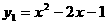 上的点(1,a)
上的点(1,a)
 把
把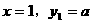 代入
代入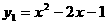 ,得
,得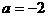
把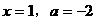 代入
代入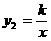 ,得
,得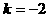
所以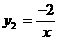
画出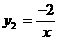 的图象如图所示.
的图象如图所示.
观察图象,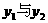 除交点(1,-2)外,还有两个交点大致为
除交点(1,-2)外,还有两个交点大致为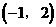 和
和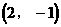
把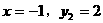 和
和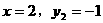 分别代入
分别代入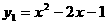 和
和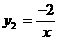 可知,
可知,
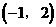 和
和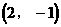 是
是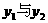 的两个交点
的两个交点
根据图象可知:当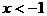 或
或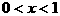 或
或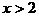 时,
时,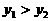
当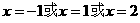 时,
时,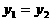
当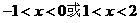 时,
时,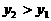
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com