
题目列表(包括答案和解析)
14(本小题满分6分)计算: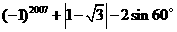 .
.
(2007江西省中考试题
答案.解:原式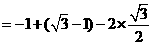 ··················· 3分
··················· 3分
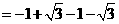 ······················· 4分
······················· 4分
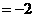 6分
6分
15.化简: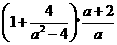 (2007江西省中考试题)
(2007江西省中考试题)
答案.解:原式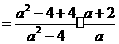 ······················ 2分
······················ 2分
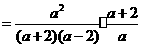 ····················· 4分
····················· 4分
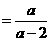 ···························· 6分
···························· 6分
这两题计算化简题母的是为了考查学生的做题细心程度
12、如图,在平面直角坐标系中,已知一圆弧过正方形
网格的格点A、B、C,已知A点的坐标为(-3,5),
则该圆弧所在圆的圆心坐标为 .
(2007湖北恩施自治州 答案: (-1,0) 本题意在考查学生对圆的特点的掌握程度。)
13一个大长方体是由四个完全一样的小长方体拼成的,如果每个小长方体的长、宽、高分别是3、1、1,那么这个大长方体的表面积可能有 种不同的值,其中最小值为 .
(2007山东青岛 答案:4 32 本题意在培养学生的实际观察和空间想象能力)
9.从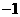 ,
,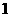 ,
,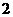 这三个数中,任取两个不同的数作为一次函数
这三个数中,任取两个不同的数作为一次函数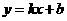 的系数
的系数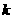 ,
,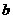 ,则一次函数
,则一次函数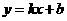 的图象不经过第四象限的概率是 .
的图象不经过第四象限的概率是 .
2007山东德州 答案: 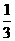 本题的目的是为了考查学生对一次函数图像的掌握情况。
本题的目的是为了考查学生对一次函数图像的掌握情况。
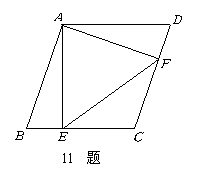 11如图,在菱形
11如图,在菱形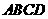 中,
中,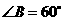 ,点
,点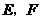 分别从点
分别从点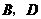 出发以同样的速度沿边
出发以同样的速度沿边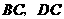 向点
向点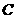 运动.给出以下四个结论:①
运动.给出以下四个结论:①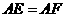 ②
②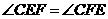 ③当点
③当点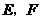 分别为边
分别为边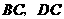 的中点时,
的中点时, 是等边三角形④当点
是等边三角形④当点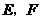 分别为边
分别为边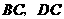 的中点时,
的中点时, 的面积最大.上述结论中正确的序号有 .(把你认为正确的序号都填上)
的面积最大.上述结论中正确的序号有 .(把你认为正确的序号都填上)
 (2007山东德州 答案:①②③.本题的目的是为了考查学生对特殊四边形的有关性质的理解程度)
(2007山东德州 答案:①②③.本题的目的是为了考查学生对特殊四边形的有关性质的理解程度)
7当x=-3时,代数式2x2+的值是__________.
(2007浙江嘉兴 答案:17 本题的目的在于考查学生对代数式的求值的掌握情况及对负整数指数幂的理解程度。)
.
8.如图,用同样规格的黑白两色的正方形瓷砖铺设矩形地面,
请观察图形并解答下列问题。
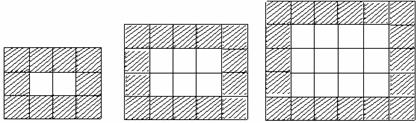
n=1 n=2 n=3
在第n个图中,共有 白块瓷砖。
(2007广东台山 答案:n(n+1)本题规律题是为了考查学生从特殐图形找出存在的一般规律)
6.有一列数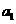 ,
,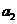 ,
,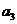 ,
, ,
,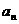 ,从第二个数开始,每一个数都等于
,从第二个数开始,每一个数都等于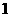 与它前面那个数的倒数的差,若
与它前面那个数的倒数的差,若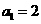 ,则
,则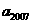 为( )
为( )
A. B.
B.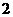 C.
C.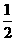 D.
D.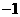
(2007扬州 答案:D 本题目的是为了发展学生能从特殊到一般找出规律)
3.反比例函数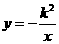 (
(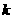 为常数,
为常数,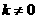 )的图象位于( )
)的图象位于( )
A.第一、二象限 B.第一、三象限
C.第二、四角限 D.第三、四象限
(2007南京 答案:C 考查学生对反比例函数特点的掌握情况,)
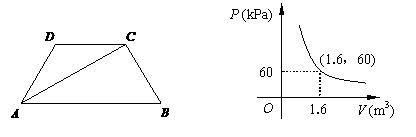 4.如图,在等腰梯形ABCD中,AB∥CD, 对角线AC平分∠BAD,∠B=60º,CD=2cm,则梯形ABCD的面积为(
)cm2.
4.如图,在等腰梯形ABCD中,AB∥CD, 对角线AC平分∠BAD,∠B=60º,CD=2cm,则梯形ABCD的面积为(
)cm2.
A.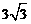 B.6 C.
B.6 C.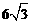 D.12
D.12
(2007山东青岛 答案:A 本题考查的内容较多等腰梯形的
有关性质,直角三角形的特点)
5用半径为 、圆心角为
、圆心角为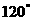 的扇形做成一个圆锥的侧面, 则这个圆锥的底面半径是……………………………………………………………………(
)
的扇形做成一个圆锥的侧面, 则这个圆锥的底面半径是……………………………………………………………………(
)
A.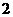 cm
B.
cm
B.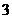 cm
C.
cm
C.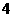 cm
D.
cm
D.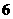 cm
cm
(2007漳州市中考试题, 答案:A 本题考查学生对圆锥侧面展开图及扇形与圆之间的联系,发展学生的空间想象能力。)
(2007无锡 答案:B 本题意在考查学生对一元二次方程的解的方法,锻炼学生在解决问题时考虑问题的严密性)
2. 下图所示的几何体的主视图是 ( )
下图所示的几何体的主视图是 ( )
A. B. C. D. (第2题图)
(2007孝感市 答案:A目的是考查学生对三视图的掌握情况和立体图形的认识,了解数学与我们实际生活紧密相联系。)
1.计算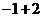 的值是( )
的值是( )
A.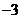 B.
B.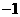 C.
C.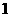 D.
D.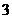
(2007临沂 答案:B 目的是考查学生对简单有理数加减运算是否能够掌握,让学生对数学中考试题有一定的理解,在下面做题过程中对考试不产生惧怕心理。)
28.如图,将边长为4的正方形纸片,置于平面直角坐标系内,顶点A在坐标原点,AB在x轴正方向上,E、F分别是AD、BC的中点,M在DC上,将△ADM沿折痕AM折叠,使点D折叠后恰好落在EF上的P点处.
(1)求点M、P的坐标;
(2)求折痕AM所在直线的解析式.
(3)设点H为直线AM上的点,是否存在这样的点H,使得以H、A、P为顶点的三角形为等腰三角形,若存在,请直接写出点H的坐标;若不存在,请说明理由.
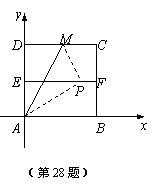
[命题意图]考察函数的有关内容。
[参考答案]解:(1)依据题意
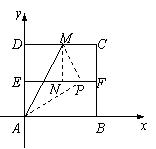 ∵AP=AD=4,AE=2
∵AP=AD=4,AE=2
∴EP=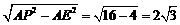
∴P点坐标为(2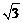 ,2)……………3分
,2)……………3分
设DM=x,则MP=x,过M作MN⊥EF,垂足为N,
则 MN=2,PN=2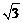 -x
-x
在Rt△MNP中,22+(2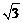 -x)2=x2
-x)2=x2
解之得:x=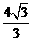
∴M点坐标为(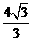 ,4) …………………………………6分
,4) …………………………………6分
(2)设折痕AM所在直线的解析式为y=kx(k≠0),则4=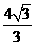 k
k
k=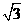 ∴折痕AM所在直线的解析式为y=
∴折痕AM所在直线的解析式为y=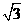 x ………………8分
x ………………8分
(3)
H1(-2,-2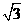 )H2(
)H2(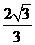 ,2),H3(2,2
,2),H3(2,2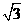 ),H4(2
),H4(2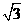 ,6)
,6)
…………14分
[试题来源]资料
本资料由《七彩教育网》 提供!
(第27题12分,第28题14分)
27.九(1)班数学兴趣小组在社会实践活动中,进行了如下的课题研究:用一定长度的铝合金材料,将它设计成外观为长方形的三种框架,使长方形框架面积最大.
小组讨论后,同学们做了以下三种试验:
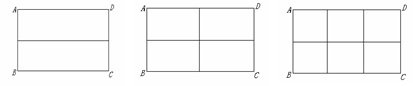
图案(1) 图案(2) 图案(3)
请根据以上图案回答下列问题:
(1)在图案(1)中,如果铝合金材料总长度(图中所有黑线的长度和)为6m,当AB为1m,
长方形框架ABCD的面积是____________ m2;
(2)在图案(2)中,如果铝合金材料总长度为6m,设AB为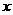 m,长方形框架ABCD的面积为S= ________(用含
m,长方形框架ABCD的面积为S= ________(用含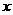 的代数式表示);当AB=_________m时, 长方形框架ABCD的面积S最大;
的代数式表示);当AB=_________m时, 长方形框架ABCD的面积S最大;
在图案(3)中,如果铝合金材料总长度为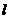 m, 设AB为
m, 设AB为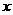 m,当AB=________m时, 长方形框架ABCD的面积S最大.
m,当AB=________m时, 长方形框架ABCD的面积S最大.
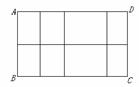 (3)经过这三种情形的试验,他们发现对于图案(4)这样的情形也存在着一定的规律。探索: 如图案(4), 如果铝合金材料总长度为
(3)经过这三种情形的试验,他们发现对于图案(4)这样的情形也存在着一定的规律。探索: 如图案(4), 如果铝合金材料总长度为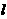 m共有n条竖档时, 那么当竖档AB为多少时,长方形框架ABCD的面积最大.
m共有n条竖档时, 那么当竖档AB为多少时,长方形框架ABCD的面积最大.
图案(4)
[命题意图]将图形和实际生活联系在一起。
[参考答案]解:(1)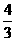 ,
……………………2分
,
……………………2分
(2)-x2+2x
,1,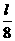 ,
……………8分
,
……………8分
(3)设AB长为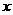 m,那么AD为
m,那么AD为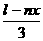 ,…………… 9分
,…………… 9分
S=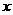 ·
·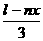 =-
=-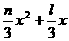 , ……………………11分
, ……………………11分
当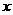 =
=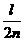 时,S最大. ……………………………… 12分
时,S最大. ……………………………… 12分
[试题来源]资料
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com