
题目列表(包括答案和解析)
3.下列运算正确的是 ( )
A.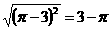 B.
B.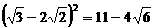
C.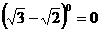 D.
D.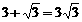
2.国家体育场“鸟巢”为2008年第29届奥林匹克运动会的主体育场,总占地面积21公顷,建筑面积258,000m2.奥运会、残奥会开闭幕式、田径比赛及足球比赛决赛都是在“鸟巢”举行的.其中258,000用科学计数法表示为 ( )
A.2.58×104 B.2.60×105 C.0.258×106 D.2.58×105
1.- 的相反数为 ( )
A.-2 B.2 C. D.-
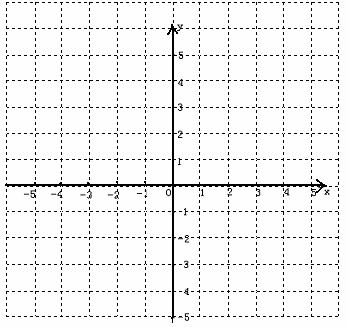
28.(本题12分)如图, 在平面直角坐标系中, 以点M(0, 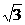 )为圆心, 以2
)为圆心, 以2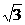 为半径作⊙M交x轴于A、B两点, 交y轴的负半轴于点C, 连结AM、 AC 、AD.
为半径作⊙M交x轴于A、B两点, 交y轴的负半轴于点C, 连结AM、 AC 、AD.
(1)设L是过点A的直线,它与⊙M相交于点N,若△ 是等腰三角形,则满中条件的直线L有几条?试写出所有满足条件的L的解析式,并在图②中画出直线L.(如果不止一条,则可以用L1 、L2 、L 3,…表示);(4分)
是等腰三角形,则满中条件的直线L有几条?试写出所有满足条件的L的解析式,并在图②中画出直线L.(如果不止一条,则可以用L1 、L2 、L 3,…表示);(4分)
(2)在(1)的条件下,若直线L是某个一次函数的图象,它与y轴交于点S,连接MN,并且不再连接其它点,问是否存在一个三角形,使它总与△ 相似,证明你的结论;(4分)
相似,证明你的结论;(4分)
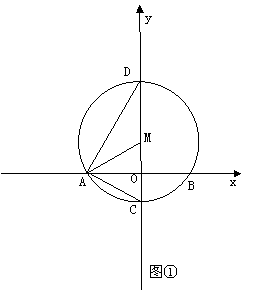
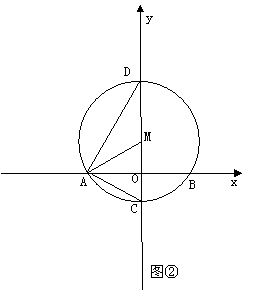 (3)在(2)的条件下求线段SM的长. (4分)
(3)在(2)的条件下求线段SM的长. (4分)
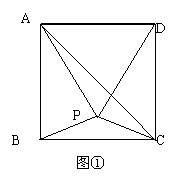
27.(本题12分)如图1,在正方形ABCD内有一点P满足AP=AB,PB=PC,连结AC、PD.
(1)求证:△APB≌△DPC;(3分)
(2)求证:∠PAC=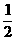 ∠BAP;(4分)
∠BAP;(4分)
(3)若将原题中的正方形ABCD变为等腰梯形ABCD(如图2),AD∥BC,且BA=AD=DC,形内一点P仍满足AP=AB,PB=PC,试问(2)中结论还成立吗?若成立请给予证明;若不成立,请说明理由.(5分)
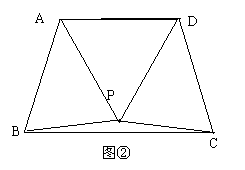
26.(本题10分)已知反比例函数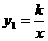 和二次函数
和二次函数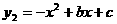 的图象都过点A
的图象都过点A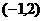
(1)求k的值及b、c的数量关系式(用c的代数式表示b)(3分)
(2)若两函数的图象除公共点A外,另外还有两个公共点B(m,1)、C(1,n),试在如图所示的直角坐标系中画出这两个函数的图象,并利用图象回答,x为何值时,y1>y2. (5分)
(3)当c值满足什么条件时,函数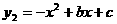 在
在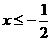 的范围内随x的增大而增大?(3分)
的范围内随x的增大而增大?(3分)
25.(本题8分,1+1+1+3+2)
问题1
如图①,一张三角形ABC纸片,点D、E分别是△ABC边上两点 .
研究(1):如果沿直线DE折叠,使A点落在CE上,则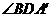 与∠A的数量关系是___________
与∠A的数量关系是___________
研究(2):如果折成图②的形状,猜想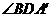 、
、 和∠A的数量关系是_______________
和∠A的数量关系是_______________
研究(3):如果折成图③的形状,猜想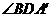 、
、 和∠A的数量关系,并说明理由。
和∠A的数量关系,并说明理由。
猜想:__________________ 理由:
问题2
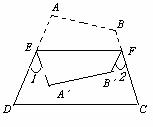 研究(4):将问题1推广,如图,将四边形ABCD纸片沿EF折叠,使点A、B落在四边形EFCD的内部时,
研究(4):将问题1推广,如图,将四边形ABCD纸片沿EF折叠,使点A、B落在四边形EFCD的内部时,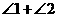 与
与 、
、 之间的数量关系是_____________________
之间的数量关系是_____________________
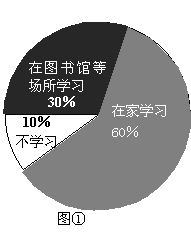
24.(本题10分)望海社区调查社区居民双休日的学习状况,采取下列调查方式:①从一幢高层住宅楼中选取200名居民;②从不同住宅楼中随机选取200名居民;③选取社区内的200名在校学生.
(1)上述调查方式最合理的是_______________(填序号);(2分)
(2)将最合理的调查方式得到的数据制成扇形统计图(如图①)和频数分布直方图(如图②)
①请补全直方图(直接画在图②中);(2分)
②在这次调查中,200名居民中,在家学习的有___________人;(2分)
(3)请估计该社区2000名居民中双休日学习时间不少于4h的人数是________人;(2分)
(4)小明的叔叔住在该社区,那么双休日他去叔叔家时,正好叔叔不学习的概率是______.(1分)
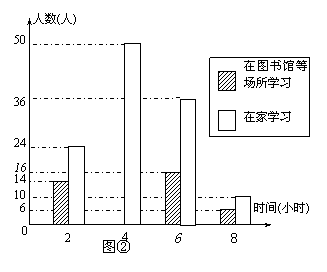
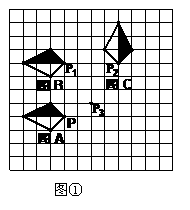
23.(本题10分)如图,是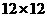 的正方形(每个小正方形边长均为1个单位)的网格.
的正方形(每个小正方形边长均为1个单位)的网格.
(1)在图①中建立适当的直角坐标系使点P1, P3的坐标分别为(-1,2)、(1,-1).将图A通过平移或旋转这两种变换得到图C可用以下三种办法:
(1)方法1:将图形A 向 (填“上”或“下”)平移 个单位,得到图形B,再将图形B 向 右平移4个单位后,再绕点 按_________时针方向旋转________°得到图形C;(5分)
方法2:先将图形A平移到图形B,再将图形B绕某点Q顺时针旋转90°得到图形C,则点Q的坐标是 ;(1分)
方法3:直接将图形A绕某点R顺时针旋转 °得到图形C,则点R的坐标是 ;(2分)
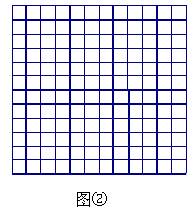
(2)在图②中画一个格点四边形EFGH,使它为轴对称图形且面积等于图A面积的3倍(除矩形外);(2分)
22.(本题8分)桌面上放有4张卡片,正面分别标有数字1,2,3,4,这些卡片除数字外完全相同,把这些卡片反面朝上洗均匀后放在桌面上,甲从中任意抽出一张,记下卡片上的数字后仍按反面朝上放回洗匀,乙从中再任意抽出一张,记下卡片上的数字,最后将甲、乙所记下的两数相加;
(1)用列表或画树状图的方法求两数相加的和为5的概率;(4分)
(2)若甲与乙按上述方式做游戏,当两数之和大于5时,甲胜;反之则乙胜。这个游戏对双方是否公平?请说明理由.若游戏对双方不公平,请制定得分规则使游戏对双方公平.(4分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com