
题目列表(包括答案和解析)
3.考试时不能使用计算器,所有答案都必须做在答题卷标定的位置上,请务必注意标角、连线等均要求在答题卷上。
2.答题时, 应该在答题卷指定位置写明校名、 姓名、班级和考试序号等。
1. 本试卷分试题卷和答题卷两部分。满分120分, 考试时间120分钟,本次考试采用闭卷形式。
25.(本题满分8分)
解:(1)∵ 点A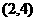 在抛物线C1上,
在抛物线C1上,
∴ 把点A坐标代入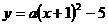 得
得 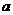 =1 ……………………………………(2分)
=1 ……………………………………(2分)
∴ 抛物线C1的解析式为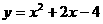
设B(-2,b), ∴ b=-4, ∴ B(-2,-4) …………………………(3分)
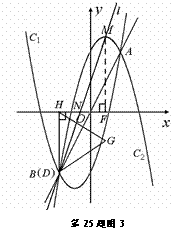
(2)①如图1:
∵ M(1, 5),D(1, 2), 且DH⊥x轴,∴ 点M在DH上,MH=5.
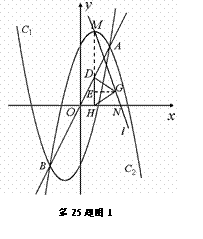 过点G作GE⊥DH,垂足为E,
过点G作GE⊥DH,垂足为E,
由△DHG是正三角形,可得EG=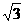 , EH=1,
, EH=1,
∴ ME=4. ………………………………(4分)
设N ( x, 0 ), 则 NH=x-1,
由△MEG∽△MHN,得 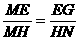 ,
,
∴ 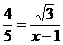 , ∴
, ∴ 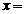
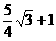 …………(5分))
…………(5分))
∴ 点N的横坐标为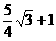 .
.
② 当点D移到与点A重合时,如图2,
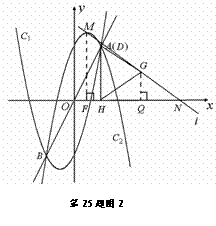 直线
直线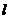 与DG交于点G,此时点N的横坐标最大.
与DG交于点G,此时点N的横坐标最大.
过点G,M作x轴的垂线,垂足分别为点Q,F,
设N(x,0)
∵ A (2, 4) ∴ G (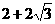 , 2)
, 2)
∴ NQ=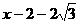 NF =
NF =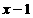 GQ=2 MF =5.
GQ=2 MF =5.
∵ △NGQ∽△NMF
∴ 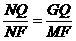
∴ 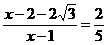
∴ 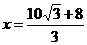 . ………………………………………………………(7分)
. ………………………………………………………(7分)
当点D移到与点B重合时,如图3
 直线
直线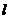 与DG交于点D,即点B
与DG交于点D,即点B
此时点N的横坐标最小.
∵ B(-2, -4) ∴ H(-2, 0), D(-2, -4)
设N(x,0)
∵ △BHN∽△MFN, ∴ 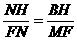
∴ 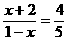 ∴
∴ 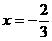
∴ 点N横坐标的范围为 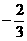 ≤x≤
≤x≤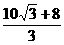 ………………………………(8分)
………………………………(8分)
(注:本卷中许多问题解法不唯一,请老师根据评分标准酌情给分)
23. (本题满分7分)
解:(1)根据题意,得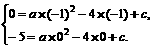 …(2分)
…(2分)
解得 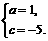 ……………………(3分)
……………………(3分)
∴二次函数的表达式为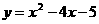 .
.
B(5,0)…………………………………………………………………………(4分)
(2)令y=0,得二次函数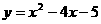 的图象与x轴
的图象与x轴
的另一个交点坐标C(5, 0)…………………………………………………(5分)
由于P(2,-2) ,符合条件的坐标有共有4个,分别是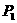 (4,0)
(4,0)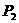 (2,0)
(2,0) 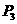 (-2
(-2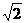 ,0)
,0) 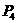 ( 2
( 2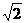 ,0) ………………………………………………………………………(7分)
,0) ………………………………………………………………………(7分)
④ 24. (本题满分6分)
解:(1)证明: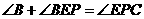
而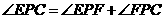
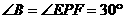
所以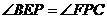
由 可知
可知
结论成立. ………………………………………………………………………(3分)
(2)相似……………………………………………………………………………(4分)
‚相似……………………………………………………………………………(5分)
理由:由△BPE与△CFP相似可得
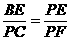 即
即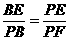 ,而
,而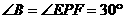 知结论成立…………(6分)
知结论成立…………(6分)
③由△BPE与△PFE相似得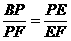 ,即
,即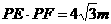 ,过F作PE垂线可得
,过F作PE垂线可得

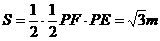
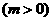 ………………………………………………(7分)
………………………………………………(7分)

图a 图b
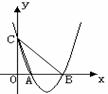
22.(本题满分4分)
 解:(1)
解:(1)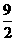
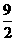 ………………………(2分)
………………………(2分)
(2)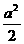 …………(2分)
…………(2分)
结论是:三角形DBF的面积的大小只与a有关, 与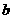 无关.
无关.
(没写结论也不扣分)
21. (本题满分6分)
(本题满分6分)
解:(1)令x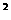 -4x + 3=0,
-4x + 3=0,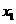 =1,
=1,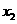 =3………………………(2分)
=3………………………(2分)
则A(1,0) B(3,0) C(0,3)
BC所在直线为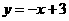 ……………………………………………(3分)
……………………………………………(3分)
(2)反比例函数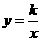 与BC有两个交点且k为正整数
与BC有两个交点且k为正整数
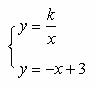
整理得:x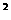 -3x + k=0………………………(4分)
-3x + k=0………………………(4分)
∵△=9-4k>0 ∴ k<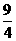 …………………………………………………(5分)
…………………………………………………(5分)
又因为反比例函数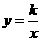 与BC的交点 所以k>0,因为 k为正整数
与BC的交点 所以k>0,因为 k为正整数
所以k=1或k=2………………………………………(6分)
20.解法一:求两个班人均捐款各多少元?
设1班人均捐款x元,则2班人均捐款(x+4)元,根据题意得
·90%= ………………………………………………………(3分)
解得x=36 经检验x=36是原方程的根,且符合实际意义………………………(4分)
∴x+4=40 ……………………………………………(5分)
答:1班人均捐36元,2班人均捐40元
解法二:求两个班人数各多少人?
设1班有x人,则根据题意得
+4= …………(3分)
解得x=50 ,经检验x=50是原方程的根,且符合实际意义…(4分)
∴90x % =45 ……………(5分)
答:1班有50人,2班有45人.
(不检验扣1分)
20.(本题满分5分)
19.证明:连结OC,∵OA=OC ∴∠OAC=∠OCA……………(1分)
∵DC是切线
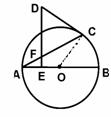 ∴∠DCF=900-∠OCA……………(2分)
∴∠DCF=900-∠OCA……………(2分)
∵DE⊥AB
∴∠DFC=900-∠OAC……………(3分)
∵∠OAC=∠OCA,……………(4分)
∴∠DFC=∠DCF……………(5分)即△DFC是等腰三角形.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com