
题目列表(包括答案和解析)
2.如图,点 是△
是△ 的边
的边 的延长线上 一点,
的延长线上 一点, ∥
∥ .
.
若 ,
, ,则
,则 的度数等于
的度数等于
A. B.
B. C.
C. D.
D.
1.计算 的结果是
的结果是
 A.-6
A.-6  B.9 C.-9
D.6
B.9 C.-9
D.6
25、(本小题满分14分)
如图,△ABC中AB=AC,BC=6, ,点P从点B出发沿射线BA移动,同时,点Q从点C出发沿线段AC的延长线移动,已知点P、Q移动的速度相同,PQ与直线BC相交于点D.
,点P从点B出发沿射线BA移动,同时,点Q从点C出发沿线段AC的延长线移动,已知点P、Q移动的速度相同,PQ与直线BC相交于点D.
(1)如图①,当点P为AB的中点时,求CD的长;
 (2)如图②,过点P作直线BC的垂线垂足为E,当点P、Q在移动的过程中,线段BE、DE、CD中是否存在长度保持不变的线段?请说明理由;
(2)如图②,过点P作直线BC的垂线垂足为E,当点P、Q在移动的过程中,线段BE、DE、CD中是否存在长度保持不变的线段?请说明理由;
① ②
24、 (本题14分)
如图,在平面直角坐标系xoy中,抛物线 与x轴的交点为点A,与y轴的交点为点B,过点B作x轴的平行线BC,交抛物线于点C,连结AC.现有两动点P,Q分别从O,C两点同时出发,点P以每秒4个单位的速度沿OA向终点A移动,点Q以每秒1个单位的速度沿CB向点B移动,点P停止运动时,点Q也同时停止运动,线段OC,PQ相交于点D,过点D作DE∥OA,交CA于点E,射线QE交x轴于点F.设动点P,Q移动的时间为t(单位:秒)
与x轴的交点为点A,与y轴的交点为点B,过点B作x轴的平行线BC,交抛物线于点C,连结AC.现有两动点P,Q分别从O,C两点同时出发,点P以每秒4个单位的速度沿OA向终点A移动,点Q以每秒1个单位的速度沿CB向点B移动,点P停止运动时,点Q也同时停止运动,线段OC,PQ相交于点D,过点D作DE∥OA,交CA于点E,射线QE交x轴于点F.设动点P,Q移动的时间为t(单位:秒)
(1)求A,B,C三点的坐标和抛物线的顶点的坐标;
(2)当t为何值时,四边形PQCA为平行四边形?请写出计算过程;
(3)当0<t<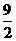 时,△PQF的面积是否总为定值?若是,求出此定值,若不是,请说明理由;
时,△PQF的面积是否总为定值?若是,求出此定值,若不是,请说明理由;
(4)当t为何值时,△PQF为等腰三角形?请写出解答过程.

23、(本题12分)
如图(1),凸四边形 ,如果点
,如果点 满足
满足 ,且
,且 ,则称点
,则称点 为四边形
为四边形 的一个半等角点.
的一个半等角点.
(1)在图(3)正方形 内画一个半等角点
内画一个半等角点 ,且满足
,且满足 .
.
(2)在图(4)四边形 中画出一个半等角点
中画出一个半等角点 ,保留画图痕迹(不需写出画法).
,保留画图痕迹(不需写出画法).
(3)若四边形 有两个半等角点
有两个半等角点 (如图(2)),证明线段
(如图(2)),证明线段 上任一点也是它的半等角点.
上任一点也是它的半等角点.

解:

(3)
22、(本题12分)
为了扶持大学生自主创业,市政府提供了80万元无息贷款,用于某大学生开办公司生产并销售自主研发的一种电子产品,并约定用该公司经营的利润逐步偿还无息贷款.已知该产品的生产成本为每件40元,员工每人每月的工资为2500元,公司每月需支付其它费用15万元.该产品每月销售量 (万件)与销售单价
(万件)与销售单价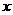 (元)之间的函数关系如图所示.
(元)之间的函数关系如图所示.
(1)求月销售量 (万件)与销售单价
(万件)与销售单价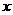 (元)之间的函数关系式;
(元)之间的函数关系式;
(2)当销售单价定为50元时,为保证公司月利润达到5万元(利润=销售额-生产成本-员工工资-其它费用),该公司可安排员工多少人?
(3)若该公司有80名员工,则该公司最早可在几个月后还清无息贷款?

21、(本题12分)
如图, 的直径
的直径 和
和 是它的两条切线,
是它的两条切线, 切
切 于E,交AM于D,
于E,交AM于D,
 交BN 于C.设
交BN 于C.设 .
.
 (1)求证:
(1)求证: ;
;
(2)求 关于
关于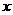 的关系式;
的关系式;
(3)求四边形 的面积S,并证明:
的面积S,并证明: .
.
|
20、(本题10分)
 已知:如图,在直角梯形ABCD中,AD∥BC,∠ABC=90°,DE⊥AC于点F,交BC于点G,交AB的延长线于点E,且
已知:如图,在直角梯形ABCD中,AD∥BC,∠ABC=90°,DE⊥AC于点F,交BC于点G,交AB的延长线于点E,且 .
.
(1)求证: ;
;
(2)若 ,求AB的长.
,求AB的长.
19.(本题10分)
如图所示,矩形 的周长为14cm,
的周长为14cm, 为
为 的中点,以
的中点,以 为圆心,
为圆心, 长为半径画弧交
长为半径画弧交 于点
于点 .以
.以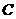 为圆心,
为圆心, 长为半径画弧交
长为半径画弧交 于点
于点 .当
.当 时,求AB,BC的长度.
时,求AB,BC的长度.

18、(本题9分)
田忌赛马是一个为人熟知的故事,传说战国时期,齐王与田忌各有上、中、下三匹马,同等级的马中,齐王的马比田忌的马强.有一天,齐王要与田忌赛马,双方约定:比赛三局,每局各出一匹,每匹马赛一次,蠃得两局者为胜.看样子田忌似乎没有什么胜的希望,但是田忌的谋士了解到主人的上、中等马分别比齐王的中、下等马要强
(1)如果齐王将马按上中下的顺序出阵比赛,那么田忌的马如何出阵,田忌才能取胜?
(2)如果齐王将马按上中下的顺序出阵,而田忌的马随机出阵比赛,田忌获胜的概率是多少?(要求写出双方对阵的所有情况)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com