
题目列表(包括答案和解析)
8.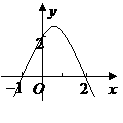 如图,抛物线与两坐标轴的交点分别为(-1,0),(2,0),(0,2),则当
如图,抛物线与两坐标轴的交点分别为(-1,0),(2,0),(0,2),则当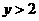 时,
时,
自变量x的取值范围是( ▲ )
A.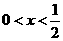 B.
B. 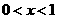
C.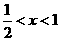 D.
D.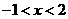 (第8题图)
(第8题图)
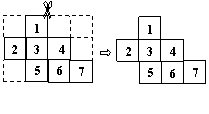
7.如图,将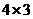 的网格图剪去5个小正方形后,图中还剩下7个小正方形,为了使余下
的网格图剪去5个小正方形后,图中还剩下7个小正方形,为了使余下
的部分(小正方形之间至少要有一条边相连)恰好能折成一个正方体,需要再剪去1个
小正方形,则应剪去的小正方形的编号是( ▲ )
A. 7 B.6 C. 5 D. 4
6.如图,已知⊙O的半径为10,弦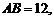
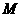 是
是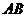 上任意一点,则线段
上任意一点,则线段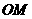 的长可能
的长可能
是( ▲ )
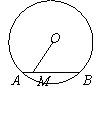 A.5 B.7
C.9 D.11
A.5 B.7
C.9 D.11
(第5题图) (第6题图) (第7题图)
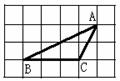
5.如图,△ABC的顶点都是正方形网格中的格点,则cos∠ABC等于( ▲ )
A. 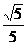 B.
B.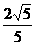 C.
C.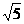 D.
D.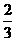
4.在下列图形中,既是中心对称图形又是轴对称图形的是( ▲ )
A. 等边三角形 B. 平行四边形 C.等腰梯形 D.菱形
3.生物学家发现一种病毒的长度约为0.000043毫米,数据0.000043用科学记数法表示的结果为( ▲ )
A.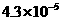 B.
B.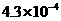 C.
C.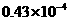 D.
D.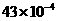
2.下面是一位同学做的四道题: ①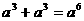 ;②
;②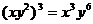 ;③
;③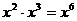 ;④
;④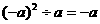 . 其中做对的一道题是( ▲ )
. 其中做对的一道题是( ▲ )
A.① B.② C.③ D.④
1.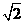 的相反数是( ▲ )
的相反数是( ▲ )
A.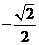 B.
B.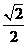 C.
C.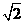 D.
D.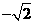
25.(本题满分14分,第(1)小题4分,第(2)小题5分,第(3)小题5分)
已知:在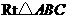 中,∠ACB=90°,BC=6,AC=8,过点
中,∠ACB=90°,BC=6,AC=8,过点 作直线MN⊥AC,点E是直线MN上的一个动点,
作直线MN⊥AC,点E是直线MN上的一个动点,
(1)如图1,如果点E是射线AM上的一个动点(不与点A重合),联结CE交AB于点P.若AE为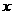 ,AP为
,AP为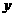 ,求y关于x的函数解析式,并写出它的定义域;
,求y关于x的函数解析式,并写出它的定义域;
(2) 在射线AM上是否存在一点E,使以点E、A、P组成的三角形与△ABC相似,若存在求AE的长,若不存在,请说明理由;
(3)如图2,过点B作BD⊥MN,垂足为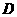 ,以点C为圆心,若以AC为半径的⊙C与以ED为半径的⊙E相切,求⊙E的半径.
,以点C为圆心,若以AC为半径的⊙C与以ED为半径的⊙E相切,求⊙E的半径.


24.(本题满分12分,每小题各4分)
 已知,矩形OABC在平面直角坐标系中位置如图所示,A的坐标
已知,矩形OABC在平面直角坐标系中位置如图所示,A的坐标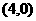 ,C的坐标
,C的坐标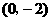 ,直线
,直线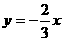 与边BC相交于点D,
与边BC相交于点D,
(1)求点D的坐标;
(2)抛物线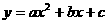 经过点A、D、O,求此抛物线的表达式;
经过点A、D、O,求此抛物线的表达式;
(3)在这个抛物线上是否存在点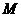 ,使
,使 、
、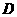 、
、 、
、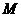 为
为
顶点的四边形是梯形?若存在,请求出所有符合条件的点 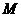 的坐标;
的坐标;
若不存在,请说明理由。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com