
题目列表(包括答案和解析)
2.实数a,b在数轴上对应点的位置如图所示,则下列各式正确的是 ( )
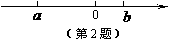 A.a>b
B. a>-b
A.a>b
B. a>-b
C.-a>b D.-a<-b
1.下列运算正确的是 ( )
A. 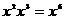 B.
B.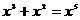 C.
C.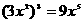 D.
D.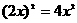 .
.
28.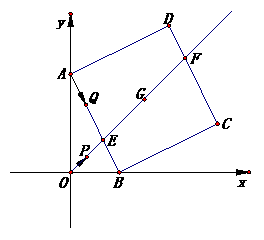 (本题满分10分)如图,G为正方形ABCD的对称中心,A(0,2),B(1,0),直线OG交AB于E,DC于F,点Q从A出发沿A→B→C的方向以
(本题满分10分)如图,G为正方形ABCD的对称中心,A(0,2),B(1,0),直线OG交AB于E,DC于F,点Q从A出发沿A→B→C的方向以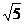 个单位每秒速度运动,同时,点P从O出发沿OF方向以
个单位每秒速度运动,同时,点P从O出发沿OF方向以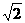 个单位每秒速度运动,Q点到达终点,点P停止运动,运动时间为t。求:
个单位每秒速度运动,Q点到达终点,点P停止运动,运动时间为t。求:
(1)求G点的坐标。
(2)当t为何值时,△AEO与△DFP相似?
(3)求△QCP面积S与t的函数关系式;
27、(本题满分10分)如图,菱形ABCD的顶点A、B两点的坐标分别为(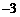 ,0)、
,0)、
(0,4),抛物线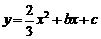 经过B点,且顶点在直线
经过B点,且顶点在直线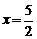 上.
上.
(1)求抛物线对应的函数关系式,并说明此抛物线一定过点C、D;
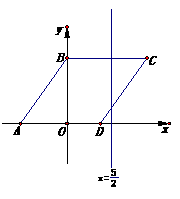 (2)若M点是该抛物线上位于C、D之间的一动点,求△CDM面积的最大值.
(2)若M点是该抛物线上位于C、D之间的一动点,求△CDM面积的最大值.
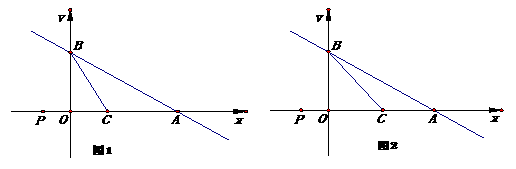
26.(本题满分10分)如图1,直线y=-x+3与x轴、y轴交于A、B两点,C点为线
段AO上一点,一动点P在x轴上.
(1)当P点运动到与原点O重合时,P点关于直线BC的对称点恰好落在直线AB上,
求此时PC的长;
(2)如图2,若C点为线段AO的中点,问:P点运动到何处,点P关于直线BC的
对称点落在直线AB上?
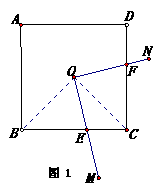
25.(本题满分10分)(1)如图1,在正方形ABCD中,O为正方形的中心,∠MON绕着O点自由的转动,角的两边与正方形的边BC、CD交于E、F.若∠MON=90°,正方形的面积等于S.求四边形OECF的面积.(用S表示)
下面给出一种求解的思路,你可以按这一思路求解,也可以选择另外的方法去求.
解:连结OB、OC.∵O为正方形的中心,∴∠BOC=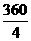 =90°,
=90°,
∵∠MON=90°∴∠FOC+∠EOC =∠EOB+∠EOC =90°.∴∠FOC=∠EOB由无锡市天一实验学校金杨建录制 QQ:623300747.转载请注明!
 (下面请你完成余下的解题过程)
(下面请你完成余下的解题过程)
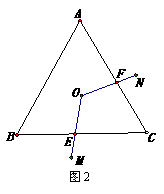
(2)若将(1)中的“正方形ABCD”改为“正三角形ABC”(如图2),O是△ABC的中
心,∠MON=120°,正三角形ABC的面积等于S.求四边形OECF的面积.(用S表
示)
(3)若将(1)中的“正方形ABCD”改为“正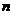 边形ABCD…X”,正
边形ABCD…X”,正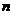 边形的面积等
边形的面积等
于S.请你作出猜想:当∠MON= °时,四边形OECF的面积= (用S表示,
并直接写出答案,不需要证明)
24.(本题满分8分)某商场销售某种商品,第一个月将此商品的进价加价20%作为销售价,共获利6000元;第二个月商场搞促销活动,将商品的进价加价10%作为销售价,第二个月的销售量比第一个月增加了100件,并且商场第二个月比第一个月多获利
2000元,求此商品的进价.
23.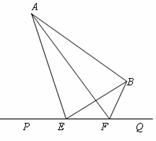 (本题满分8分)如图,大海中有A和B两个岛屿,为测量它们之间的距离,在海岸
(本题满分8分)如图,大海中有A和B两个岛屿,为测量它们之间的距离,在海岸
线PQ上点E处测得∠AEP=74°,∠BEQ=30°;在点F处测得∠AFP=60°,∠BFQ
=60°,EF=1km.
(1)判断线段AB与AE的数量关系,并说明理由;
(2)求两个岛屿A和B之间的距离(结果精确到0.1km).
22.(本题满分6分)在学校组织的“喜迎奥运,知荣明耻,文明出行”的知识竞赛中,每班参加比赛的人数相同,成绩分为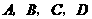 四个等级,其中相应等级的得分依次记为100分,90分,80分,70分,学校将某年级的一班和二班的成绩整理并绘制成如下的统计图:
四个等级,其中相应等级的得分依次记为100分,90分,80分,70分,学校将某年级的一班和二班的成绩整理并绘制成如下的统计图:
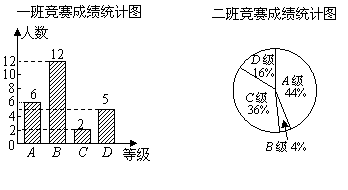
请你根据以上提供的信息解答下列问题:
(1)此次竞赛中二班成绩在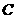 级以上(包括
级以上(包括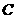 级)的人数为
;
级)的人数为
;
(2)请你将表格补充完整:
|
|
平均数(分) |
中位数(分) |
众数(分) |
|
一班 |
87.6 |
90 |
|
|
二班 |
87.6 |
|
100 |
(3)请从下列不同角度对这次竞赛成绩的结果进行分析:
①从平均数和中位数的角度来比较一班和二班的成绩;
②从平均数和众数的角度来比较一班和二班的成绩;
③从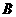 级以上(包括
级以上(包括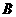 级)的人数的角度来比较一班和二班的成绩.
级)的人数的角度来比较一班和二班的成绩.
21.(本题满分6分)“五·一”期间,某书城为了吸引读者,设
立了一个可以自由转动的转盘(如图,转盘被平均分成12份),并
规定:读者每购买100元的书,就可获得一次转动转盘的机会,如
果转盘停止后,指针正好对准红色、黄色、绿色区域,那么读者就
可以分别获得45元、30元、25元的购书券,凭购书券可以在书城
继续购书.如果读者不愿意转转盘,那么可以直接获得10元的购书
券.
(1)写出转动一次转盘获得45元购书券的概率;
(2)转转盘和直接获得购书券,你认为哪种方式对读者更合算?请说明理由.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com