
题目列表(包括答案和解析)
2.到三角形各顶点的距离相等的点是三角形( )
A.三条角平分线的交点 B.三条高的交点
 C.三边的垂直平分线的交点 D.三条中线的交点
C.三边的垂直平分线的交点 D.三条中线的交点
1.25的算术平方根是
 A. 5 B.±5 C.
A. 5 B.±5 C.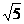 D.±
D.±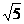
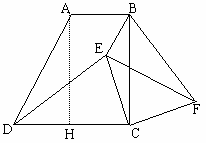
证明:作AH⊥CD于H,
∵梯形ABCD中,∠BCD=90°,tan∠ADC=2,即∠ADC≠90°.
∴ AB∥CD,AH=BC,AB=CH. …………………………………………2分
又∵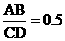 ,即CH+DH=2AB=2CH
,即CH+DH=2AB=2CH
∴ DH=CH,CD=2DH.
∵ tan∠ADC=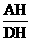 =2,
=2,
∴ AH=2DH=CD=BC. …………………………………………3分
 在△EDC和△FBC中,
在△EDC和△FBC中,
又∵∠EDC=∠FBC,DE=BF,
∴△EDC≌△FBC.
∴CE=CF, ∠ECD=∠FCB.
∵∠ECD+∠ECB=∠BCD=90°,
∴∠FCB+∠ECB=90°,即∠ECF=90°.
∴△ECF是等腰直角三角形. ……………………………………4分
⑵ ∵ 在等腰Rt△ECF中,∠ECF=90°,
∴ ∠CEF=45°,CE=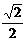 EF. ………………………………………5分
EF. ………………………………………5分
又∵∠BEC=135°,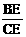 =0.5 ,
=0.5 ,
∴ ∠BEF=90°,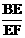 =
=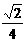 .
…………………………
.
………………………… ……………6分
……………6分
不妨设BE=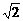 ,EF= 4,则BF=
,EF= 4,则BF=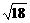 .
.
∴sin∠BFE=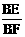 =
=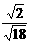 =
=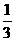 .
………………………………………7分
.
………………………………………7分
∴∠A=∠B=∠C=60°, BC=CA=AB=1. …………………………………1分
又∵∠BEP=∠CFE=∠FQA=90°, BP=x.
∴BE=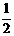 x,
CE=1-
x,
CE=1-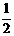 x,
CF=
x,
CF=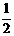 -
-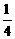 x,
AF=1-(
x,
AF=1-(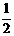 -
-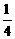 x)=
x)=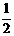 +
+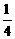 x.
x.
∴AQ=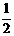 AF=
AF=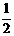 (
(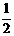 +
+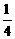 x),
x),
∴ y=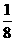 x+
x+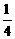 .
…………………………………………2分
.
…………………………………………2分
⑵由方程组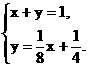 …………………………………………3分
…………………………………………3分
得x
=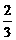 .
……………………………………………4分
.
……………………………………………4分
∴当点P和点Q重合时,x =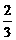 ,
,
 ∴EF=
∴EF=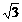 CF=
CF=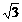 (
(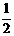 -
-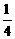 x)=
x)=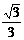 . …………………………………………5分
. …………………………………………5分
⑶设线段PE、FQ相交于点M,
易证△MEF是等边三角形, …………………………………………6分
且当点P和点A重合时,EF最短为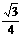 .
……………………………7分
.
……………………………7分
∴ 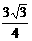 ≤ m <
≤ m <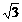 .
…………………………………………8分
.
…………………………………………8分
Δ=4 (k+2)2-32k
=4k2-16k+16
=4 (k-2)2 . ………………………………………………1分
∵ 当k≠2时,4 (k-2)2>0,
∴方程x2-2(k+2) x+8k=0有两个不相等的实数根.
∴ 当k≠2时,抛物线C与x轴必定交于两点. …………………………2分
⑵ 解方程x2-2(k+2) x+8k=0,
得 x1=4,x2=2k. ………………………………………………3分
∵点A、B在y轴两侧,且A在B的左边,
∴k<0,点B(4,0). ………………………………………………4分
把点B(4,0)代入y=x-3k+6,
得 k=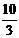 >0,与“k<0”不符.
>0,与“k<0”不符.
∴ 直线l不可能经过点B. ………………………………………………5分
⑶ y=x2-2(k+2) x+8k
=[x-(k+2)]2-(k-2)2,
作MH⊥x轴于H,则MH=(k-2)2. ………………………………………6分
∵k<0, ∴-3k+6>0.
∴OP= -3k+6.
由S△ABP=S△ABM  ,得 -3k+6=(k-2)2
…………………………………7分
,得 -3k+6=(k-2)2
…………………………………7分
解得 k1= -1,k2= 2(舍去)
∴存在实数k= -1,使得S△ABP=S△ABM .
此时,抛物线C的解析式是y=x2-2x-8. …………………………………8分
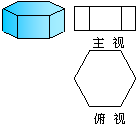
22. 第2次划分,共有9个正方形; …………………………………………1分
第100次划分后,共有401个正方形; ………………………………………2分
依题意,第n次划分后,图中共有4n+1个正方形, …………………………3分
而方程4n+1=2011没有整数解,
所以,不能得到2011个正方形.  …………………………………………4分
…………………………………………4分
21. ⑴ 是
…………………………………………1分
⑴ 是
…………………………………………1分
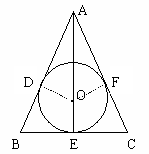
理由是:∵⊙O与AB相切,把切点记作D.
 联结OD,则OD⊥AB于D. 作OF⊥AC于F,
联结OD,则OD⊥AB于D. 作OF⊥AC于F,
∵AE是底边BC上的高,
∴AE也是顶角∠BAC的平分线.
∴OF=OD=r为⊙O的半径.
∴⊙O与AC相切于F.
又∵ ⊙O与BC相切,
∴⊙O是△ABC的内切圆. ………………………………………………2分
⑵ ∵OE⊥BC于E,
∴点E是切点,即OE=r.
由题意,AB=5,BE=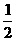 AB=2,
AB=2,
∴ AE=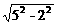 =
=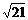 .
………………………………………3分
.
………………………………………3分
∵Rt△AOD∽Rt△ABE,
∴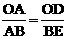 ,
………………………………………………4分
,
………………………………………………4分
即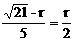 .
.
解得,r=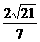 .
.
∴ ⊙O的半径是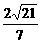 .
……………………………………………5分
.
……………………………………………5分
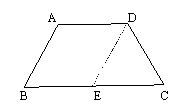 作DE∥AB交BC与E,则∠DEC=∠B=60°, ………………………2分
作DE∥AB交BC与E,则∠DEC=∠B=60°, ………………………2分
又∵在等腰梯形ABCD中,AD∥BC.
∴ DE=AB =CD,且AD=BE .
∴△CDE是等边三角形.
又∵AB =AD,
∴CE=CD=AD=BE=AB. ………………………………………………3分
依题意,AB+AD+CD+CE+BE=12cm, ………………………………4分
即 5BE=12cm ,
∴ BE=2.4cm
∴ BC边的长为4.8cm. ………………………………………………5分
20. ⑴ 500 ………………………………………………1分
⑵ 4880 ………………………………………………2分
⑶ 表中空格填“20”  ………………………………………………3分
………………………………………………3分
把扇形统计图补全 ………………………………………………5分
18. ⑴ 由题意,可认定点A的坐标是(-1, 2),
把x = -1, y=2代入y=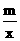 ,
,
解得m= -2.
∴ 反比例函数的解析式是y=
-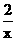 .
………………………………2分
.
………………………………2分
⑵ 点B (2, -1). ……………………………………………3分
⑶ 把点A(-1,2)、B (2, -1)分别代入y=kx+b,
得 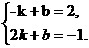 ……………………………………………4分
……………………………………………4分
解得,k= -1,b=1. ……………………………………………5分
17. 设骑自行车学生的速度是x千米/时. ………………………………1分
依题意,得 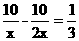 .
……………………………………2分
.
……………………………………2分
解得 x=15. ……………………………………3分
经检验, x=15是原分式方程的根. ……………………………………4分
 答: 骑自行车同学的速度是15千米/时. ………………………………5分
答: 骑自行车同学的速度是15千米/时. ………………………………5分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com