
题目列表(包括答案和解析)
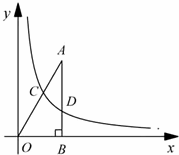
18、(2011•苏州)如图,已知点A的坐标为( ,3),AB丄x轴,垂足为B,连接OA,反比例函数y=
,3),AB丄x轴,垂足为B,连接OA,反比例函数y=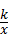 (k>0)的图象与线段OA、AB分别交于点C、D.若AB=3BD,以点C为圆心,CA的
(k>0)的图象与线段OA、AB分别交于点C、D.若AB=3BD,以点C为圆心,CA的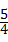 倍的长为半径作圆,则该圆与x轴的位置关系是 相交 (填”相离”,“相切”或“相交“).
倍的长为半径作圆,则该圆与x轴的位置关系是 相交 (填”相离”,“相切”或“相交“).
考点:直线与圆的位置关系;反比例函数图象上点的坐标特征。
分析:根据D点的坐标为( ,1),得出反比例函数y=
,1),得出反比例函数y=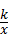 解析式,再根据A点坐标得出AO直线解析式,进而得出两图象的交点坐标,进而得出AC的长度,再利用直线与圆的位置关系得出答案.
解析式,再根据A点坐标得出AO直线解析式,进而得出两图象的交点坐标,进而得出AC的长度,再利用直线与圆的位置关系得出答案.
解答:解:∵已知点A的坐标为( ,3),AB=3BD,
,3),AB=3BD,
∴AB=3,BD=1,
∴D点的坐标为( ,1),
,1),
∴反比例函数y=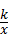 解析式为:
解析式为:
y=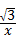 ,
,
∴AO直线解析式为:y=kx,
3= k,
k,
∴k= ,
,
∴y= x,
x,
∴直线y= x与反比例函数y=
x与反比例函数y=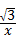 的交点坐标为:
的交点坐标为:
x=±1,
∴C点的横坐标为1,
纵坐标为: ,
,
CO=2,
∴AC=2 ﹣2,
﹣2,
∴CA的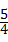 倍=
倍=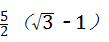 ,
,
CE= ,
,
∵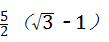 ﹣
﹣ =
=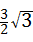 ﹣
﹣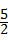 >0,
>0,
∴该圆与x轴的位置关系是相交.
故答案为:相交.
点评:此题主要考查了直线与圆的位置关系以及反比例函数的性质以及直线与反比例函数交点坐标的求法,综合性较强得出AC的长是解决问题的关键.
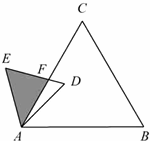
17、(2011•苏州)如图,巳知△ABC是面积为 的等边三角形,△ABC∽△ADE,AB=2AD,∠BAD=45°,AC与DE相交于点F,则△AEF的面积等于
的等边三角形,△ABC∽△ADE,AB=2AD,∠BAD=45°,AC与DE相交于点F,则△AEF的面积等于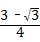 (结果保留根号).
(结果保留根号).
考点:相似三角形的性质;等边三角形的性质。
专题:计算题。
分析:根据相似三角形面积比等于相似比的平方求得三角形ADE的面积,再根据求出其边长,可根据三角函数得出三角形面积.
解答:解:∵△ABC∽△ADE,AB=2AD,
∴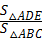 =
=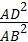 ,
,
∵AB=2AD,S△ABC= ,
,
∴S△ADE=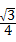 ,
,
在△EAD中,连接HF,则∠AFH=45°,∠EFH=30°,
设AH=HF=x,则EH=xtan30°=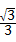 x.
x.
又∵S△ADE=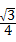 ,
,
∴AE=1,
∴x+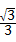 x=1,
x=1,
解得x=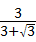 =
=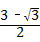 .
.
∴S△AEF=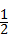 ×1×
×1×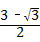 =
=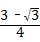 .
.

点评:此题主要考查相似三角形的判定与性质和等边三角形的性质等知识点,解得此题的关键是根据相似三角形面积比等于相似比的平方求得三角形ADE的面积,然后问题可解.
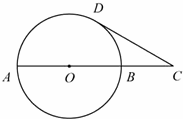
16、(2011•苏州)如图,巳知AB是⊙O的一条直径,延长AB至C点,使得AC=3BC,CD与⊙O相切,切点为D.若CD= ,则线段BC的长度等于 1 .
,则线段BC的长度等于 1 .
考点:切线的性质;勾股定理。
分析:根据切割线定理:从圆外一点引圆的切线和割线,切线长是这点到割线与圆交点的两条线段长的比例中项,即可求解.
解答:解:∵CD与⊙O相切,切点为D,
∴CD2=BC•AC,
即CD2=BC•3BC=3,
解得:BC=1.
故答案是:1.
点评:本题主要考查了切割线定理,正确理解定理是解题的关键.
15、(2011•苏州)巳知a、b是一元二次方程x2﹣2x﹣1=0的两个实数根,则代数式(a﹣b)(a+b﹣2)+ab的值等于 ﹣1 .
考点:根与系数的关系。
专题:计算题。
分析:欲求(a﹣b)(a+b﹣2)+ab的值,先把此代数式变形为两根之积或两根之和的形式,代入数值计算即可.
解答:解:∵a、b是一元二次方程x2﹣2x﹣1=0的两个实数根,
∴ab=﹣1,a+b=2,
∴(a﹣b)(a+b﹣2)+ab
=(a﹣b)(2﹣2)+ab,
=0+ab,
=﹣1,
故答案为:﹣1.
点评:此题主要考查了根与系数的关系,将根与系数的关系与代数式变形相结合解题是一种经常使用的解题方法.
14、(2011•苏州)函数y=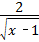 的自变量x的取值范闱是 x>1 .
的自变量x的取值范闱是 x>1 .
考点:函数自变量的取值范围。
专题:计算题。
分析:一般地从两个角度考虑:分式的分母不为0;偶次根式被开方数大于或等于0;当一个式子中同时出现这两点时,应该是取让两个条件都满足的公共部分.
解答:解:根据题意得到:x﹣1>0,
解得x>1.
故答案为:x>1.
点评:本题考查了函数式有意义的x的取值范围.判断一个式子是否有意义,应考虑分母上若有字母,字母的取值不能使分母为零,二次根号下字母的取值应使被开方数为非负数.易错易混点:学生易对二次根式的非负性和分母不等于0混淆.
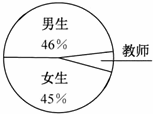
13、(2011•苏州)某初中学校的男生、女生以及教师人数的扇形统计图如图所示,若该校男生、女生以及教师的总人数为1200人,则根据图中信息,可知该校教师共有 108 人.
考点:扇形统计图。
分析:首先求得教师所占百分比,乘以总人数即可求解.
解答:解:教师所占的百分比是:1﹣46%﹣45%=9%,
则教师的人数是:1200×9%=108.
故答案是:108.
点评:本题主要考查了扇形统计图,扇形统计图直接反映部分占总体的百分比大小.
12、(2011•苏州)如图,在四边形ABCD中,AB∥CD,AD∥BC,AC、BD相交于点0.若AC=6,则线段AO的长度等于 3 .
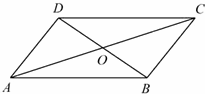
考点:平行四边形的判定与性质。
专题:计算题。
分析:根据在四边形ABCD中,AB∥CD,AD∥BC,求证四边形ABCD是平行四边形,然后即可求解.
解答:解:∵在四边形ABCD中,AB∥CD,AD∥BC,
∴四边形ABCD是平行四边形,
∵AC=6,
∴AO=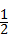 AC=
AC=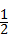 ×6=3.
×6=3.
故答案为:3.
点评:此题主要考查学生对平行四边形的判定与性质的理解和掌握,难度不大,属于基础题.
11、(2007•丽水)因式分解:a2﹣9= (a+3)(a﹣3) .
考点:因式分解-运用公式法。
分析:a2﹣9可以写成a2﹣32,符合平方差公式的特点,利用平方差公式分解即可.
解答:解:a2﹣9=(a+3)(a﹣3).
点评:本题考查了公式法分解因式,熟记平方差公式的结构特点是解题的关键.
10、(2011•苏州)如图,巳知A点坐标为(5,0),直线y=x+b(b>0)与y轴交于点B,连接AB,∠α=75°,则b的值为( )
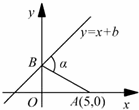
A、3 B、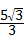
C、4 D、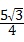
考点:一次函数综合题。
专题:综合题。
分析:根据三角函数求出点B的坐标,代入直线y=x+b(b>0),即可求得b的值.
解答:解: 由直线y=x+b(b>0),可知∠1=45°,
由直线y=x+b(b>0),可知∠1=45°,
∵∠α=75°,
∴∠ABO=180°﹣45°﹣75°=60°,
∴OB=OA÷tan∠ABO=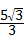 .
.
∴点B的坐标为(0,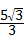 ),
),
∴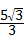 =0+b,b=
=0+b,b=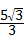 .
.
故选B.
点评:本题灵活考查了一次函数点的坐标的求法和三角函数的知识,注意直线y=x+b(b>0)与x轴的夹角为45°.
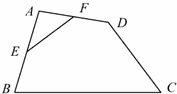
9、(2011•苏州)如图,在四边形ABCD中,E、F分別是AB、AD的中点,若EF=2,BC=5,CD=3,则tanC等于( )
A、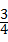 B、
B、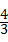
C、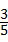 D、
D、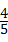
考点:锐角三角函数的定义;勾股定理的逆定理;三角形中位线定理。
专题:几何图形问题。
分析:根据三角形的中位线定理即可求得BD的长,然后根据勾股定理的逆定理即可证得△BCD是直角三角形,然后根据正切函数的定义即可求解.
解答:解: 连接BD.
连接BD.
∵E、F分別是AB、AD的中点.
∴BD=2EF=4
∵BC=5,CD=3
∴△BCD是直角三角形.
∴tanC=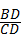 =
=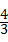
故选B.
点评:本题主要考查了三角形的中位线定义,勾股定理的逆定理,和三角函数的定义,正确证明△BCD是直角三角形是解题关键.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com