9．27的立方根为　 ▲　 ．

[答案]3。

[考点]立方根。

[分析]根据立方根的定义，直接得出结果。

8．小亮从家步行到公交车站台，等公交车去学校. 图中的

折线表示小亮的行程s(km)与所花时间t(min)之间的函

数关系. 下列说法错误的是

A．他离家8km共用了30min

B．他等公交车时间为6min

C．他步行的速度是100m/min

D．公交车的速度是350m/min

[答案]D。

[考点]二次函数。

[分析]从图可知，他离家8km共用了30min，他等公交车时间为16-10=6min，他步行的速度是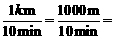100m/min，公交车的速度是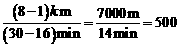m/min。二、填空题(本大题共有10小题，每小题3分，共30分．不需写出解答过程，请将答案直接写在答题卡相应位置上)

7．某市6月上旬前5天的最高气温如下(单位：℃)：28，29，31，29，32．对这组数据，下列说法正确的是

A．平均数为30　　　　 B．众数为29　　　　　　　　 C．中位数为31　　　　 D．极差为5

[答案]B。

[考点]平均数、众数、中位数、极差。

[分析]。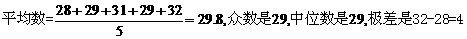

6．对于反比例函数y = ，下列说法正确的是

　 A．图象经过点(1，-1)　　　　　　　 B．图象位于第二、四象限

C．图象是中心对称图形　　　　　　　　 D．当x＜0时，y随x的增大而增大

[答案]C。

[考点]反比例函数。

[分析]根据反比例函数性质，直接得出结果。

5．若⊙O₁、⊙O₂的半径分别为4和6，圆心距O₁O₂=8，则⊙O₁与⊙O₂的位置关系是

　 A．内切　　　　　 　B．相交　　　　 　C．外切　　　　 　　D．外离

[答案]B。

[考点]圆心距。

[分析]。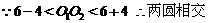

4．已知a - b =1，则代数式2a -2b -3的值是

A．-1　　　 　　　　 B．1　　 　　　　　　 C．-5　　 　　　　　 D．5

[答案]A。

[考点]代数式代换。

[分析]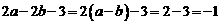

3．下面四个几何体中，俯视图为四边形的是

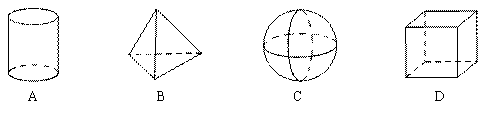
[答案]D。

[考点]几何体的三视图。

[分析]根据几何体的三视图，直接得出结果。

2．下列运算正确的是

A．x²+ x³ = x⁵　　　　　　 B．x⁴·x² = x⁶　　　　　　 C．x⁶÷x² = x³ D．( x² )³ = x⁸

[答案]B。

[考点]同底幂的乘法。

[分析]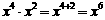

1．-2的绝对值是

A．-2　　　　　　　　　　　　 B．- 　　　　　　　　　　　 C．2　　　　　　　　　　　　 D．

[答案]C。

[考点]绝对值。

[分析]根据绝对值的定义，直接得出结果。

29、(2011•苏州)巳知二次函数y=a(x²﹣6x+8)(a＞0)的图象与x轴分别交于点A、B，与y轴交于点C．点D是抛物线的顶点．

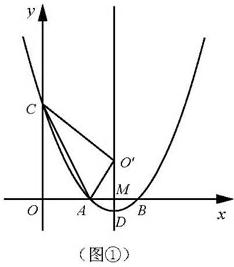
(1)如图①．连接AC，将△OAC沿直线AC翻折，若点O的对应点0'恰好落在该抛物线的 对称轴上，求实数a的值；

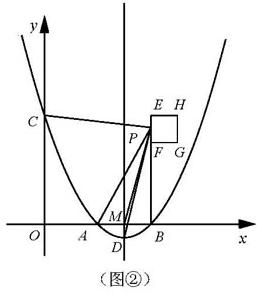
(2)如图②，在正方形EFGH中，点E、F的坐标分别是(4，4)、(4，3)，边HG位于边EF的 右侧．小林同学经过探索后发现了一个正确的命题：“若点P是边EH或边HG上的任意一点，则四条线段PA、PB、PC、PD不能与任何一个平行四边形的四条边对应相等 (即这四条线段不能构成平行四边形)．“若点P是边EF或边FG上的任意一点，刚才的结论是否也成立？请你积极探索，并写出探索过程；

(3)如图②，当点P在抛物线对称轴上时，设点P的纵坐标l是大于3的常数，试问：是否存在一个正数阿a，使得四条线段PA、PB、PC、PD与一个平行四边形的四条边对应相等 (即这四条线段能构成平行四边形)？请说明理由．

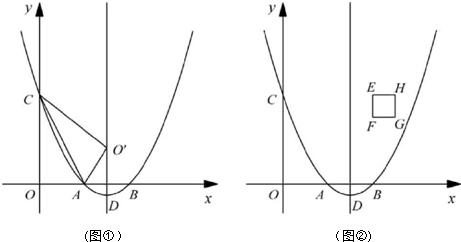
考点：二次函数综合题。

分析：(1)本题需先求出抛物线与x轴交点坐标和对称轴，再根据∠OAC=60°得出AO，从而求出a．

(2)本题需先分两种情况进行讨论，当P是EF上任意一点时，可得PC＞PB，从而得出PB≠PA，PB≠PC，PB≠PD，即可求出线段PA、PB、PC、PD不能构成平行四边形．

(3)本题需先得出PA=PB，再由PC=PD，列出关于t与a的方程，从而得出a的值，即可求出答案．

解答：解：(1)令y=0，由a(x²﹣6x+8)=0，

解得x₁=2，x₂=4；

令x=0，解得y=8a，

∴点 A、B、C的坐标分别是(2，0)、(4，0)、(0，8a)，

该抛物线对称轴为直线x=3，

∴OA=2，

如图①，设抛物线对称轴与x轴的交点为M，则AM=1，

由题意得：O′A=OA=2，

∴O′A=2AM，

∴∠O′AM=60°，

∴∠OAC=∠O′AC60°，

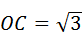∴，AO=2，

即8a=2，

∴a=；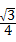

(2)若点P是边EF或边FG上的任意一点，结论同样成立，

①如图②，设P是边EF上的任意一点(不与点E重合)，连接PM，

∵点E(4，4)、F(4，3)与点B(4，0)在一直线上，点C在y轴上，

∴PB＜4，PC≥4，

∴PC＞PB，

又PD＞PM＞PB，PA＞PM＞PB，

∴PB≠PA，PB≠PC，PB≠PD，

∴此时线段PA、PB、PC、PD不能构成平行四边形，

②设P是边FG上的任意一点(不与点G重合)，

∵点F的坐标是(4，3)，点G的坐标是(5，3)，

∴FG=3，GB=，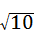

∴3≤PB，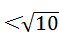

∵PC≥4，

∴PC＞PB，

又PD＞PM＞PB，PA＞PM＞PB，

∴PB≠PA，PB≠PC，PB≠PD，

∴此时线段PA、PB、PC、PD也不能构成平行四边形；

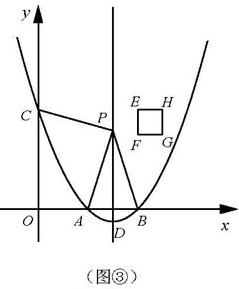
(3)存在一个正数a，使得线段PA、PB、PC、PD能构成一个平行四边形，

如图③，∵点A、B是抛物线与x轴交点，点P在抛物线对称轴上，

∴PA=PB，

∴当PC=PD时，线段PA、PB、PC、PD能构成一个平行四边形，

∵点C的坐标是(0，8a)，点D的坐标是(3，﹣a)，

点P的坐标是(3，t)，

∴PC²=3²+(t﹣8a)²，PD²=(t+a)²，

由PC=PD得PC²=PD²，

∴3²+(t﹣8a)²=(t+a)²，

整理得：7a²﹣2ta+1=0有两个不相等的实数根a==，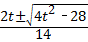

显然a=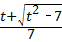满足题意

当t是一个大于3的常数时，存在一个正数a=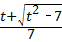，使得线段PA、旁边、PC、PD能构成一个平行四边形．

点评：本题主要考查了二次函数的综合问题，在解题时要注意运用数形结合和分类讨论，把二次函数的图象与性质和平行四边形的判定相结合是本题的关键．