
题目列表(包括答案和解析)
22、(1)提示:∵PQ∥FN,PW∥MN ∴∠QPW =∠PWF,∠PWF =∠MNF ∴∠QPW =∠MNF
同理可得:∠PQW =∠NFM或∠PWQ =∠NFM ∴△FMN∽△QWP
(2)当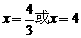 时,△PQW为直角三角形;
时,△PQW为直角三角形;
当0≤x<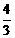 ,
,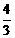 <x<4时,△PQW不为直角三角形。(3)
<x<4时,△PQW不为直角三角形。(3)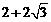
22.(2011年广东省)如图(1),(2)所示,矩形ABCD的边长AB=6,BC=4,点F在DC上,DF=2。动点M、N分别从点D、B同时出发,沿射线DA、线段BA向点A的方向运动(点M可运动到DA的延长线上),当动点N运动到点A时,M、N两点同时停止运动。连接FM、FN,当F、N、M不在同一直线时,可得△FMN,过△FMN三边的中点作△PQW。设动点M、N的速度都是1个单位/秒,M、N运动的时间为x秒。试解答下列问题:
(1)说明△FMN∽△QWP;
(2)设0≤x≤4(即M从D到A运动的时间段)。试问x为何值时,△PQW为直角三角形?
当x在何范围时,△PQW不为直角三角形?
 (3)问当x为何值时,线段MN最短?求此时MN的值。
(3)问当x为何值时,线段MN最短?求此时MN的值。

24.(本小题满分l4分)
解:(1)∵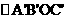 由
由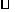 ABOC旋转得到,且点A的坐标为(0,3),
ABOC旋转得到,且点A的坐标为(0,3),
点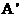 的坐标为(3,0)。
的坐标为(3,0)。
所以抛物线过点C(-1,0),A(0,3),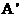 (3,0)设抛物线的解析式为
(3,0)设抛物线的解析式为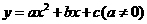 ,可得
,可得
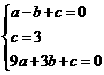 解得
解得
∴过点C,A,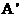 的抛物线的解析式为
的抛物线的解析式为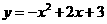 。
。
(2)因为AB∥CO,所以∠OAB=∠AOC=90°。
 ∴
∴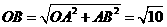 ,又
,又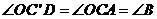 .
.
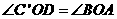 ,∴
,∴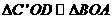 又
又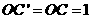 ,
,
∴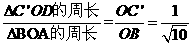 ,又△ABO的周长为
,又△ABO的周长为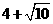 。
。
∴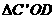 的周长为
的周长为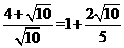 。
。
(3)连接OM,设M点的坐标为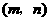 ,
,
∵点M在抛物线上,∴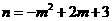 。
。
∴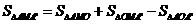
=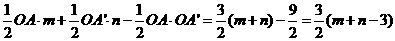
=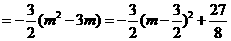
因为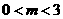 ,所以当
,所以当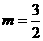 时,
时,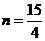 。△AMA’的面积有最大值
。△AMA’的面积有最大值
所以当点M的坐标为(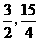 )时,△AMA’的面积有最大值,且最大值为
)时,△AMA’的面积有最大值,且最大值为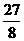 。
。
28. (1)∵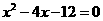 ,∴
,∴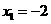 ,
,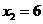 。
。
∴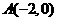 ,
,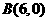 。·························1分
。·························1分
又∵抛物线过点 、
、 、
、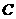 ,故设抛物线的解析式为
,故设抛物线的解析式为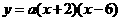 ,将点
,将点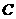 的坐标代入,求得
的坐标代入,求得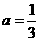 。
。
∴抛物线的解析式为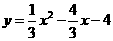 。················3分
。················3分
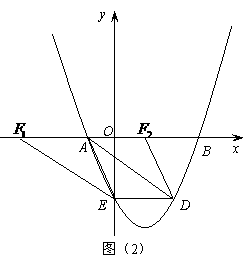
(2)设点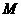 的坐标为(
的坐标为( ,0),过点
,0),过点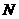 作
作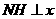 轴于点
轴于点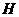 (如图(1))。
(如图(1))。
∵点 的坐标为(
的坐标为(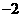 ,0),点
,0),点 的坐标为(6,0),
的坐标为(6,0),
∴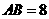 ,
,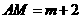 。···························4分
。···························4分
∵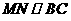 ,∴
,∴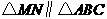 。
。
∴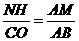 ,∴
,∴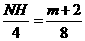 ,∴
,∴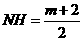 。·················5分
。·················5分
∴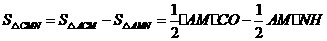
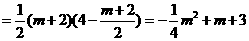 ···························6分
···························6分
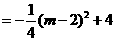 。
。
∴当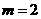 时,
时,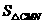 有最大值4。
有最大值4。
此时,点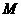 的坐标为(2,0)。·····································7分
的坐标为(2,0)。·····································7分
(3)∵点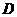 (4,
(4,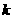 )在抛物线
)在抛物线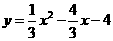 上,
上,
∴当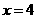 时,
时,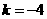 ,
,
∴点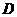 的坐标是(4,
的坐标是(4,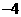 )。
)。
② 如图(2),当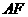 为平行四边形的边时,
为平行四边形的边时,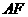


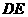 ,
,
∵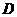 (4,
(4,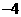 ),∴错误!链接无效。
),∴错误!链接无效。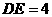 。
。
∴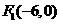 ,
,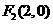 。 ···························9分
。 ···························9分
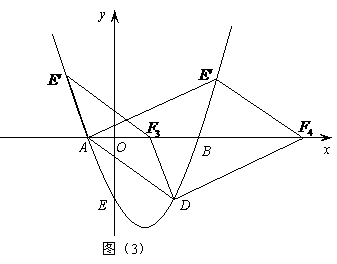
③ 如图(3),当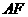 为平行四边形的对角线时,设
为平行四边形的对角线时,设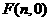 ,
,
则平行四边形的对称中心为(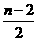 ,0)。 ··················10分
,0)。 ··················10分
∴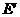 的坐标为(
的坐标为(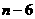 ,4)。
,4)。
把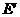 (
(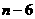 ,4)代入
,4)代入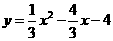 ,得
,得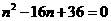 。
。
解得 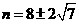 。
。
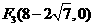 ,
,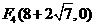 。·························12分
。·························12分
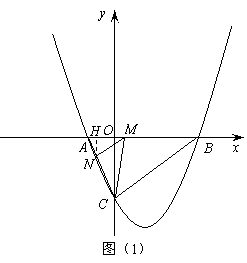
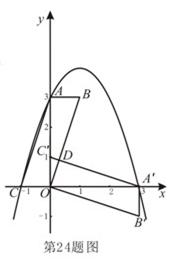
(芜湖2011)本小题满分14分)
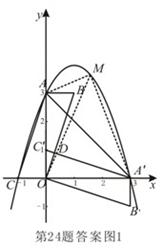
平面直角坐标系中,平行四边形ABOC如图放置,点A、C的坐标分别为(0,3)、(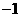 ,0),将此平行四边形绕点0顺时针旋转90°,得到平行四边形
,0),将此平行四边形绕点0顺时针旋转90°,得到平行四边形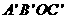 。
。
(1)若抛物线过点C,A,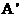 ,求此抛物线的解析式;
,求此抛物线的解析式;
(2)求平行四边形ABOC和平行四边形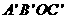 重叠部分△
重叠部分△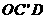 的周长;
的周长;
(3)点M是第一象限内抛物线上的一动点,间:点M在何处时△ 的面积最大?最大面积是多少?并求出此时点M的坐标。
的面积最大?最大面积是多少?并求出此时点M的坐标。
24、(1)解法1:由题意易知:△BOC∽△COA
∴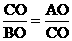 ,即
,即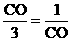
∴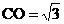
∴点C的坐标是(0,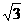 )
)
由题意,可设抛物线的函数解析式为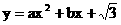
把A(1,0),B(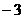 ,0)的坐标分别代入
,0)的坐标分别代入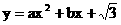 ,得
,得
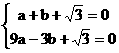
解这个方程组,得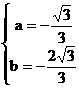
∴抛物线的函数解析式为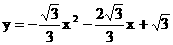
解法2:由勾股定理,得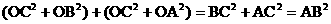
又∵OB=3,OA=1,AB=4
∴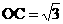
∴点C的坐标是(0,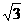 )
)
由题意可设抛物线的函数解析式为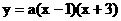 ,把C(0,
,把C(0,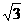 )代入
)代入
函数解析式得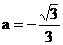
所以,抛物线的函数解析式为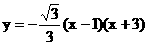
(2)解法1:截得三条线段的数量关系为KD=DE=EF
理由如下:
可求得直线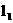 的解析式为
的解析式为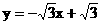 ,直线
,直线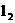 的解析式为
的解析式为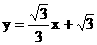
抛物线的对称轴为直线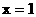
由此可求得点K的坐标为(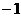 ,
,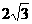 ),点D的坐标为(
),点D的坐标为(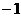 ,
,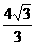 ),点E的坐标为(
),点E的坐标为(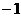 ,
,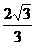 ),点F的坐标为(
),点F的坐标为(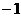 ,0)
,0)
∴KD=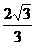 ,DE=
,DE=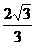 ,EF=
,EF=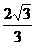
∴KD=DE=EF
解法2:截得三条线段的数量关系为KD=DE=EF
理由如下:
由题意可知Rt△ABC中,∠ABC=30°,∠CAB=60°,则可得
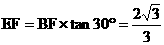 ,
,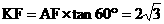 ,
,
由顶点D坐标(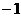 ,
,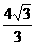 )得
)得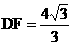
∴KD=DE=EF=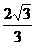
(3)解法1:(i)以点K为圆心,线段KC长为半径画圆弧,交抛物线于点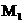 ,由抛物线对称性可知点
,由抛物线对称性可知点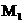 为点C关于直线
为点C关于直线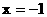 的对称点
的对称点
∴点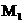 的坐标为(
的坐标为(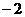 ,
,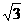 ),此时△
),此时△ 为等腰三角形
为等腰三角形
(ii)当以点C为圆心,线段CK长为半径画圆弧时,与抛物线交点为点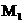 和点A,而三点A、C、K在同一直线上,不能构成三角形
和点A,而三点A、C、K在同一直线上,不能构成三角形
(iii)作线段KC的中垂线l,由点D是KE的中点,且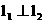 ,可知l经过点D,
,可知l经过点D,
∴KD=DC
此时,有点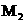 即点D坐标为(
即点D坐标为(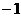 ,
,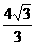 ),使△
),使△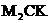 为等腰三角形;
为等腰三角形;
综上所述,当点M的坐标分别为(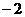 ,
,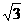 ),(
),(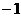 ,
,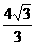 )时,△MCK为等腰三角形。
)时,△MCK为等腰三角形。
解法2:当点M的坐标分别为(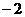 ,
,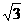 ),(
),(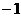 ,
,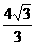 )时,△MCK为等腰三角形。
)时,△MCK为等腰三角形。
理由如下:
(i)连接BK,交抛物线于点G,易知点G的坐标为(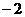 ,
,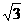 )
)
又∵点C的坐标为(0,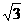 ),则GC∥AB
),则GC∥AB
∵可求得AB=BK=4,且∠ABK=60°,即△ABK为正三角形
∴△CGK为正三角形
∴当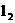 与抛物线交于点G,即
与抛物线交于点G,即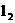 ∥AB时,符合题意,此时点
∥AB时,符合题意,此时点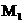 的坐标为(
的坐标为(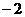 ,
,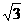 )
)
(ii)连接CD,由KD=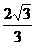 ,CK=CG=2,∠CKD=30°,易知△KDC为等腰三角形
,CK=CG=2,∠CKD=30°,易知△KDC为等腰三角形
∴当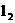 过抛物线顶点D时,符合题意,此时点
过抛物线顶点D时,符合题意,此时点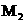 坐标为(
坐标为(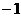 ,
,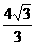 )
)
(iii)当点M在抛物线对称轴右边时,只有点M与点A重合时,满足CM=CK,但点
A、C、K在同一直线上,不能构成三角形
综上所述,当点M的坐标分别为(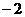 ,
,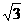 ),(
),(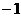 ,
,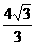 )时,△MCK为等腰三
)时,△MCK为等腰三
角形。
(2011年凉山州)如图,抛物线与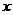 轴交于
轴交于 (
(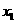 ,0)、
,0)、 (
(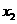 ,0)两点,且
,0)两点,且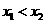 ,与
,与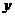 轴交于点
轴交于点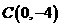 ,其中
,其中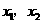 是方程
是方程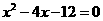 的两个根。
的两个根。
(1)求抛物线的解析式;
(2)点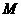 是线段
是线段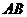 上的一个动点,过点
上的一个动点,过点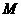 作
作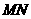 ∥
∥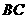 ,交
,交 于点
于点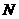 ,连接
,连接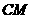 ,当
,当 的面积最大时,求点
的面积最大时,求点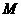 的坐标;
的坐标;
(3)点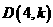 在(1)中抛物线上,点
在(1)中抛物线上,点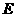 为抛物线上一动点,在
为抛物线上一动点,在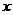 轴上是否存在点
轴上是否存在点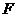 ,使以
,使以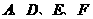 为顶点的四边形是平行四边形,如果存在,求出所有满足条件的点
为顶点的四边形是平行四边形,如果存在,求出所有满足条件的点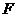 的坐标,若不存在,请说明理由。
的坐标,若不存在,请说明理由。
24、(本题12分)
 已知两直线
已知两直线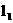 ,
,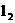 分别经过点A(1,0),点B
分别经过点A(1,0),点B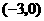 ,
,
并且当两直线同时相交于y正半轴的点C时,恰好有
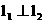 ,经过点A、B、C的抛物线的对称轴与直线
,经过点A、B、C的抛物线的对称轴与直线
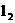 交于点K,如图所示。
交于点K,如图所示。
(1)求点C的坐标,并求出抛物线的函数解析式;
|
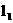 ,抛物线,直线
,抛物线,直线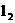 和x轴
和x轴
依次截得三条线段,问这三条线段有何数量关系?请说明理由。
(3)当直线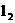 绕点C旋转时,与抛物线的另一个交点为M,请找出使△MCK为等腰三角形的点M,简述理由,并写出点M的坐标。
绕点C旋转时,与抛物线的另一个交点为M,请找出使△MCK为等腰三角形的点M,简述理由,并写出点M的坐标。
28. 解⑴①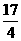 ,
,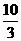 ,
,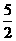 ,2,
,2,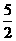 ,
,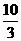 ,
,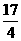 .
.
函数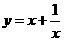
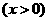 的图象如图.
的图象如图.
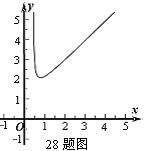
②本题答案不唯一,下列解法供参考.
当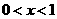 时,
时,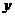 随
随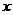 增大而减小;当
增大而减小;当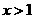 时,
时,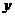 随
随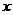 增大而增大;当
增大而增大;当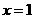 时函数
时函数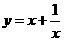
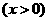 的最小值为2.
的最小值为2.
③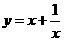
=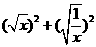
=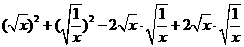
=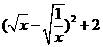
当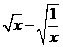 =0,即
=0,即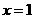 时,函数
时,函数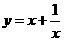
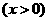 的最小值为2.
的最小值为2.
⑵当该矩形的长为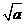 时,它的周长最小,最小值为
时,它的周长最小,最小值为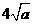 .
.
浙江省2011年初中毕业生学业考试(衢州卷)
27. 解⑴在Rt △ABC中,∠ACB=90°,CD是AB上的中线,∴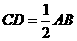 ,∴CD=BD.
,∴CD=BD.
∴∠BCE=∠ABC.∵BE⊥CD,∴∠BEC=90°,∴∠BEC=∠ACB.∴△BCE∽△ABC.
∴E是△ABC的自相似点.
⑵①作图略.
作法如下:(i)在∠ABC内,作∠CBD=∠A;
(ii)在∠ACB内,作∠BCE=∠ABC;BD交CE于点P.
则P为△ABC的自相似点.
②连接PB、PC.∵P为△ABC的内心,∴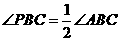 ,
,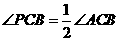 .
.
∵P为△ABC的自相似点,∴△BCP∽△ABC.
∴∠PBC=∠A,∠BCP=∠ABC=2∠PBC =2∠A,
∠ACB=2∠BCP=4∠A.∵∠A+∠ABC+∠ACB=180°.
∴∠A+2∠A+4∠A=180°.
∴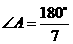 .∴该三角形三个内角的度数分别为
.∴该三角形三个内角的度数分别为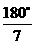 、
、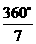 、
、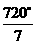 .
.
26.解⑴直线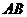 与⊙P相切.
与⊙P相切.
如图,过点P作PD⊥AB, 垂足为D.
在Rt△ABC中,∠ACB=90°,∵AC=6cm,BC=8cm,
∴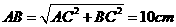 .∵P为BC的中点,∴PB=4cm.
.∵P为BC的中点,∴PB=4cm.
∵∠PDB=∠ACB=90°,∠PBD=∠ABC.∴△PBD∽△ABC.
∴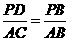 ,即
,即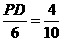 ,∴PD =2.4(cm) .
,∴PD =2.4(cm) .
当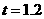 时,
时,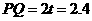 (cm)
(cm)
∴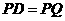 ,即圆心
,即圆心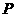 到直线
到直线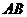 的距离等于⊙P的半径.
的距离等于⊙P的半径.
∴直线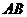 与⊙P相切.
与⊙P相切.
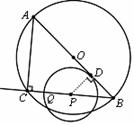
⑵ ∠ACB=90°,∴AB为△ABC的外切圆的直径.∴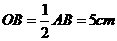 .
.
连接OP.∵P为BC的中点,∴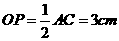 .
.
∵点P在⊙O内部,∴⊙P与⊙O只能内切.
∴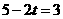 或
或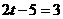 ,∴
,∴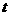 =1或4.
=1或4.
∴⊙P与⊙O相切时,t的值为1或4.
24.解:
(1)设线段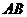 与
与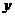 轴的交点为
轴的交点为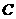 ,由抛物线的对称性可得
,由抛物线的对称性可得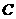 为
为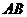 中点,
中点,

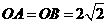 ,
,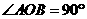 ,
,

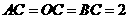 ,
,
 (
(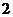 ,
,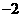 )
……… 2分
)
……… 2分
将 (
(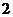 ,
,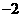 )代入抛物线
)代入抛物线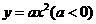 得,
得,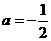 .
……… 3分
.
……… 3分
(2)解法一:过点 作
作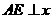 轴于点
轴于点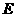 ,
,
 点
点 的横坐标为
的横坐标为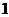 ,
,
 (1,
(1,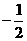 ),
……… 4分
),
……… 4分

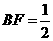 . 又
. 又
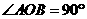 ,易知
,易知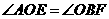 ,又
,又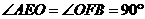 ,
,
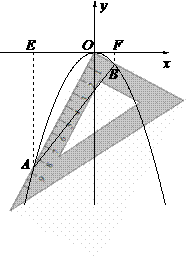
 △
△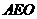 ∽△
∽△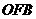 ,
,
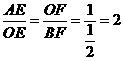

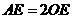 ……… 5分
……… 5分
设点 (
(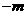 ,
,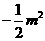 )(
)(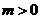 ),则
),则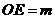 ,
,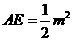 ,
,
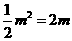

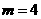 ,即点
,即点 的横坐标为
的横坐标为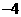 . ……… 6分
. ……… 6分
解法二:过点 作
作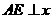 轴于点
轴于点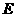 ,
,
 点
点 的横坐标为
的横坐标为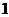 ,
,
 (1,
(1,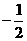 ),
……… 4分
),
……… 4分

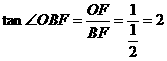

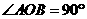 ,易知
,易知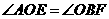 ,
,

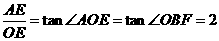 ,
,
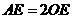 ……… 5分
……… 5分
设点 (-
(- ,
,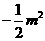 )(
)(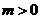 ),则
),则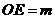 ,
,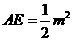 ,
,
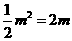

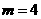 ,即点
,即点 的横坐标为
的横坐标为 .
……… 6分
.
……… 6分
解法三:过点 作
作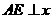 轴于点
轴于点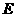 ,
,
 点
点 的横坐标为
的横坐标为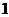 ,
,
 (1,
(1,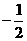 ),
……… 4分
),
……… 4分
设 (-
(- ,
,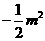 )(
)(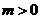 ),则
),则
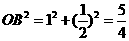 ,
,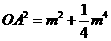 ,
,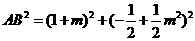 ,
,

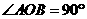

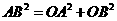 ,
,

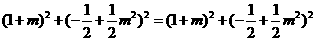 ,
,
解得: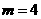 ,即点
,即点 的横坐标为
的横坐标为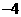 .
……… 6分
.
……… 6分
(3)解法一:设 (
(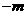 ,
,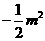 )(
)(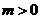 ),
), (
(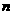 ,
,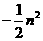 )(
)(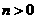 ),
),
设直线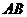 的解析式为:
的解析式为: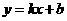 , 则
, 则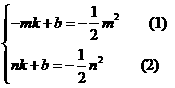 ,……… 7分
,……… 7分
 得,
得,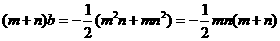 ,
,

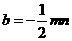 ……… 8分
……… 8分
又易知△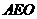 ∽△
∽△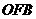 ,
,
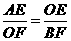 ,
,
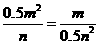 ,
,
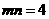 ……… 9分
……… 9分

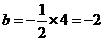 .由此可知不论
.由此可知不论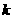 为何值,直线
为何值,直线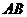 恒过点(
恒过点( ,
,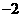 )………10分
)………10分
(说明:写出定点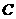 的坐标就给2分)
的坐标就给2分)
解法二:设 (
(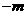 ,
,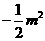 )(
)(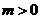 ),
), (
(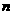 ,
,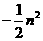 )(
)(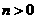 ),
),
直线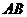 与
与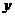 轴的交点为
轴的交点为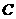 ,根据
,根据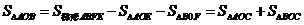 ,可得
,可得
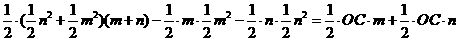 ,
,
化简,得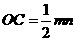 . ……… 8分
. ……… 8分
又易知△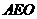 ∽△
∽△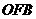 ,
,
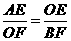 ,
,
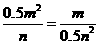 ,
,
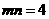 ……… 9分
……… 9分
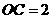 为固定值.故直线
为固定值.故直线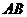 恒过其与
恒过其与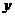 轴的交点
轴的交点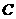 (
( ,
,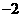 )……… 10分
)……… 10分
说明: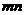 的值也可以通过以下方法求得.
的值也可以通过以下方法求得.
由前可知,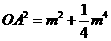 ,
,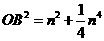 ,
,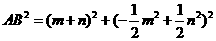 ,
,
由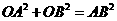 ,得:
,得: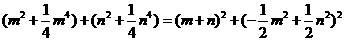 ,
,
化简,得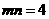 .
.
本答案仅供参考,若有其他解法,请参照本评分标准
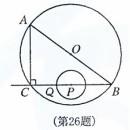
(南京市2011年)26.(8分)如图,在Rt△ABC中,∠ACB=90°,AC=6㎝,BC=8㎝,P为BC的中点.动点Q从点P出发,沿射线PC方向以2㎝/s的速度运动,以P为圆心,PQ长为半径作圆.设点Q运动的时间为t s.
⑴当t=1.2时,判断直线AB与⊙P的位置关系,并说明理由;
⑵已知⊙O为△ABC的外接圆,若⊙P与⊙O相切,求t的值.


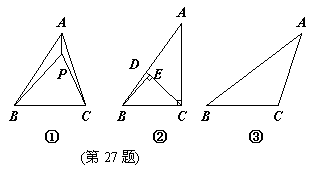
27.(9分)如图①,P为△ABC内一点,连接PA、PB、PC,在△PAB、△PBC和△PAC中,如果存在一个三角形与△ABC相似,那么就称P为△ABC的自相似点.
⑴如图②,已知Rt△ABC中,∠ACB=90°,∠ACB>∠A,CD是AB上的中线,过点B作BE⊥CD,垂足为E,试说明E是△ABC的自相似点.
⑵在△ABC中,∠A<∠B<∠C.
①如图③,利用尺规作出△ABC的自相似点P(写出作法并保留作图痕迹);
②若△ABC的内心P是该三角形的自相似点,求该三角形三个内角的度数.

28.(11分)
问题情境
已知矩形的面积为a(a为常数,a>0),当该矩形的长为多少时,它的周长最小?最小值是多少?
数学模型
设该矩形的长为x,周长为y,则y与x的函数关系式为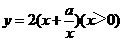 .
.
探索研究
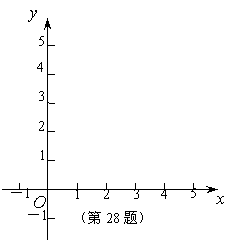 ⑴我们可以借鉴以前研究函数的经验,先探索函数
⑴我们可以借鉴以前研究函数的经验,先探索函数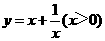 的图象性质.
的图象性质.
① 填写下表,画出函数的图象:
②
|
x |
…… |
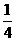 |
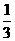 |
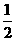 |
1 |
2 |
3 |
4 |
…… |
|
y |
…… |
|
|
|
|
|
|
|
…… |
②观察图象,写出该函数两条不同类型的性质;
③在求二次函数y=ax2+bx+c(a≠0)的最大(小)值时,除了通过观察图象,还可以通过配方得到.请你通过配方求函数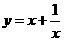 (x>0)的最小值.
(x>0)的最小值.
解决问题
⑵用上述方法解决“问题情境”中的问题,直接写出答案.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com