
题目列表(包括答案和解析)
4. (2011浙江绍兴,23,12分)数学课上,李老师出示了如下框中的题目.

小敏与同桌小聪讨论后,进行了如下解答:
(1)特殊情况,探索结论
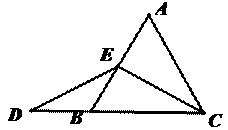
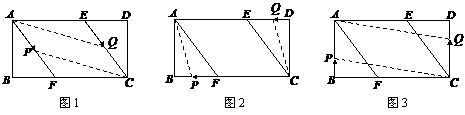
当点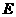 为
为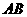 的中点时,如图1,确定线段
的中点时,如图1,确定线段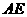 与
与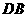 的大小关系,请你直接写出结论:
的大小关系,请你直接写出结论:
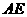
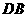 (填“>”,“<”或“=”).
(填“>”,“<”或“=”).
|
|
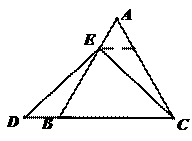
(2)特例启发,解答题目
解:题目中,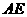 与
与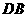 的大小关系是:
的大小关系是: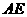
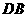 (填“>”,“<”或“=”).理由如下:如图2,过点
(填“>”,“<”或“=”).理由如下:如图2,过点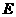 作
作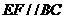 ,交
,交 于点
于点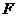 .
.
(请你完成以下解答过程)
(3)拓展结论,设计新题
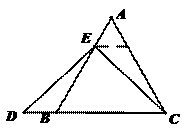
在等边三角形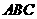 中,点
中,点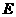 在直线
在直线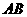 上,点
上,点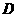 在直线
在直线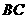 上,且
上,且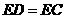 .若
.若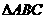 的边长为1,
的边长为1,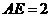 ,求
,求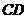 的长(请你直接写出结果).
的长(请你直接写出结果).
[答案](1)= .
(2)=.
方法一:如图,等边三角形 中,
中,
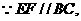
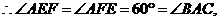
 是等边三角形,
是等边三角形,
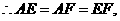
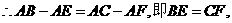
又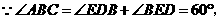
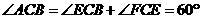
.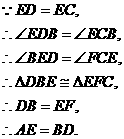
方法二:在等边三角形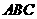 中,
中,

而由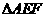 是正三角形可得
是正三角形可得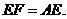
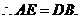
(3)1或3.
3. (2011浙江衢州,23,10分)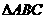 是一张等腰直角三角形纸板,
是一张等腰直角三角形纸板, .
.
要在这张纸板中剪出一个尽可能大的正方形,有甲、乙两种剪法(如图1),比较甲、乙两种剪法,哪种剪法所得的正方形面积更大?请说明理由.
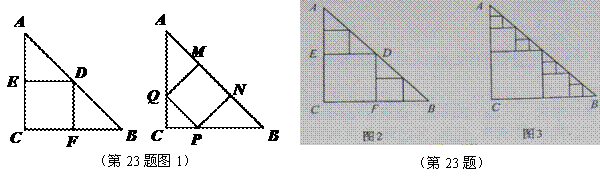

图1中甲种剪法称为第1次剪取,记所得的正方形面积为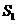 ;按照甲种剪法,在余下的
;按照甲种剪法,在余下的 中,分别剪取正方形,得到两个相同的正方形,称为第2次剪取,并记这两个正方形面积和为
中,分别剪取正方形,得到两个相同的正方形,称为第2次剪取,并记这两个正方形面积和为 (如图2),则
(如图2),则 ;再在余下的四个三角形中,用同样的方法分别剪取正方形,得到四个相同的正方形,称为第3次剪取,并记这四个正方形的面积和为
;再在余下的四个三角形中,用同样的方法分别剪取正方形,得到四个相同的正方形,称为第3次剪取,并记这四个正方形的面积和为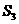 (如图3);继续操作下去…则第10次剪取时,
(如图3);继续操作下去…则第10次剪取时,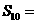 .
.
求第10次剪取后,余下的所有小三角形的面积和.
[答案](1)解法1:如图甲,由题意得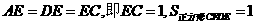 .如图乙,设
.如图乙,设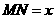 ,则由题意,得
,则由题意,得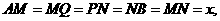
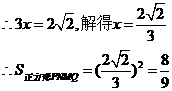
又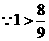
 甲种剪法所得的正方形的面积更大
甲种剪法所得的正方形的面积更大
说明:图甲可另解为:由题意得点D、E、F分别为 的中点,
的中点,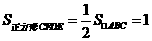
解法2:如图甲,由题意得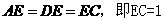
如图乙,设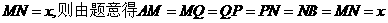
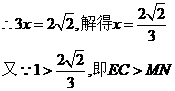
 甲种剪法所得的正方形的面积更大
甲种剪法所得的正方形的面积更大
(2)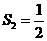
(3)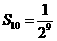
(3)解法1:探索规律可知: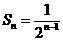 ‘
‘
剩余三角形的面积和为: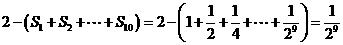
解法2:由题意可知,
第一次剪取后剩余三角形面积和为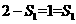
第二次剪取后剩余三角形面积和为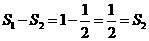
第三次剪取后剩余三角形面积和为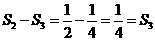
…
第十次剪取后剩余三角形面积和为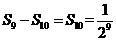

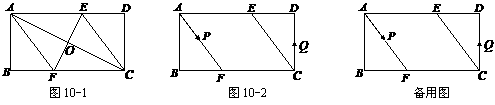
2. (2011福建福州,21,12分)已知,矩形 中,
中,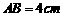 ,
,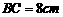 ,
,  的垂直平分线
的垂直平分线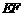 分别交
分别交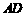 、
、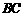 于点
于点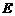 、
、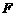 ,垂足为
,垂足为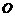 .
.
(1)如图10-1,连接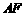 、
、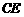 .求证四边形
.求证四边形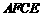 为菱形,并求
为菱形,并求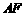 的长;
的长;
(2)如图10-2,动点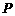 、
、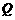 分别从
分别从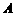 、
、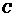 两点同时出发,沿
两点同时出发,沿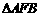 和
和 各边匀速运动一周.即点
各边匀速运动一周.即点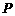 自
自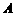 →
→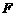 →
→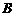 →
→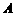 停止,点
停止,点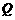 自
自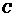 →
→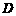 →
→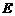 →
→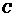 停止.在运动过程中,
停止.在运动过程中,
①已知点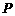 的速度为每秒5
的速度为每秒5 ,点
,点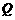 的速度为每秒4
的速度为每秒4 ,运动时间为
,运动时间为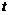 秒,当
秒,当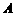 、
、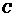 、
、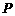 、
、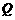 四点为顶点的四边形是平行四边形时,求
四点为顶点的四边形是平行四边形时,求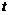 的值.
的值.
②若点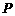 、
、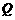 的运动路程分别为
的运动路程分别为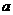 、
、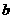 (单位:
(单位: ,
,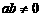 ),已知
),已知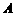 、
、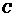 、
、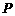 、
、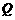 四点为顶点的四边形是平行四边形,求
四点为顶点的四边形是平行四边形,求 与
与 满足的数量关系式.
满足的数量关系式.

[答案](1)证明:①∵四边形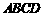 是矩形
是矩形
∴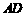 ∥
∥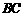
∴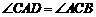 ,
,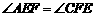
∵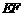 垂直平分
垂直平分 ,垂足为
,垂足为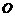
∴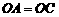
∴ ≌
≌
∴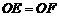
∴四边形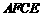 为平行四边形
为平行四边形
又∵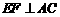
∴四边形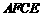 为菱形
为菱形
②设菱形的边长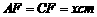 ,则
,则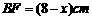
在 中,
中,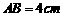
由勾股定理得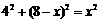 ,解得
,解得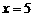
∴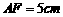
(2)①显然当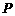 点在
点在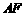 上时,
上时,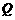 点在
点在 上,此时
上,此时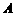 、
、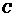 、
、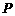 、
、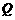 四点不可能构成平行四边形;同理
四点不可能构成平行四边形;同理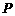 点在
点在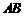 上时,
上时,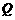 点在
点在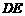 或
或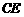 上,也不能构成平行四边形.因此只有当
上,也不能构成平行四边形.因此只有当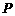 点在
点在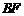 上、
上、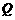 点在
点在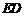 上时,才能构成平行四边形
上时,才能构成平行四边形
∴以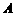 、
、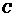 、
、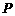 、
、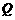 四点为顶点的四边形是平行四边形时,
四点为顶点的四边形是平行四边形时,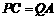
∵点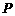 的速度为每秒5
的速度为每秒5 ,点
,点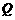 的速度为每秒4
的速度为每秒4 ,运动时间为
,运动时间为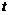 秒
秒
∴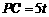 ,
,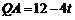
∴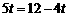 ,解得
,解得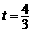
∴以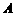 、
、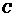 、
、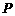 、
、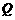 四点为顶点的四边形是平行四边形时,
四点为顶点的四边形是平行四边形时,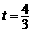 秒.
秒.
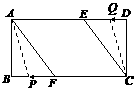

②由题意得,以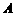 、
、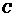 、
、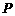 、
、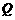 四点为顶点的四边形是平行四边形时,点
四点为顶点的四边形是平行四边形时,点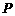 、
、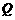 在互相平行的对应边上.
在互相平行的对应边上.
分三种情况:
i)如图1,当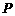 点在
点在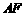 上、
上、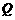 点在
点在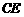 上时,
上时,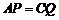 ,即
,即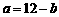 ,得
,得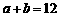
ii)如图2,当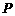 点在
点在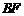 上、
上、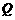 点在
点在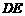 上时,
上时,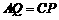 , 即
, 即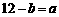 ,得
,得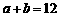
iii)如图3,当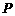 点在
点在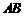 上、
上、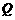 点在
点在 上时,
上时,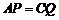 ,即
,即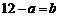 ,得
,得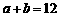
综上所述,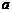 与
与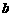 满足的数量关系式是
满足的数量关系式是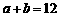
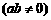

1. (2011江西南昌,25,10分)某数学兴趣小组开展了一次活动,过程如下:
设∠BAC=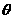 (0°<
(0°<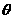 <90°).现把小棒依次摆放在两射线AB,AC之间,并使小棒两端分别落在两射线上.
<90°).现把小棒依次摆放在两射线AB,AC之间,并使小棒两端分别落在两射线上.
活动一:
如图甲所示,从点A1开始,依次向右摆放小棒,使小棒与小棒在两端点处互相垂直,A1A2为第1根小棒.
数学思考:
(1)小棒能无限摆下去吗?答: .(填“能”或“不能”)
(2)设AA1=A1A2=A2A3=1.
①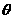 =
度;
=
度;
②若记小棒A2n-1A2n的长度为an(n为正整数,如A1A2=a1,A3A4=a2,),求此时a2,a3的值,并直接写出an(用含n的式子表示).
图甲
活动二:
如图乙所示,从点A1开始,用等长的小棒依次向右摆放,其中A1A2为第1根小棒,且A1A2= AA1.
数学思考:
(3)若已经向右摆放了3根小棒,则 = ,
= , =
,
=
,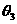 =
;(用含
=
;(用含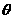 的式子表示)
的式子表示)
(4)若只能摆放4根小棒,求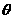 的范围.
的范围.
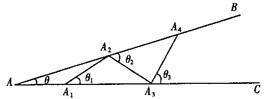
图乙
[答案]解:(1)能
(2)①22.5°
②方法一:
∵AA1=A1A2=A2A3=1, A1A2⊥A2A3,∴A1A3=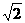 ,AA3=1+
,AA3=1+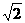 .
.
又∵A2A3⊥A3A4,∴A1A2∥A3A4.同理:A3A4∥A5A6,∴∠A=∠AA2A1=∠AA4A3=∠AA6A5,
∴AA3=A3A4,AA5=A5A6,∴a2= A3A4=AA3=1+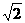 ,a3=AA3+A3A5=a2+A3A5.∵A3A5=
,a3=AA3+A3A5=a2+A3A5.∵A3A5=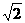 a2,
a2,
∴a3=A5A6=AA5=a2+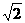 a2=(
a2=(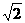 +1)2.
+1)2.
方法二:
∵AA1=A1A2=A2A3=1, A1A2⊥A2A3,∴A1A3=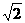 ,AA3=1+
,AA3=1+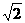 .
.
又∵A2A3⊥A3A4,∴A1A2∥A3A4.同理:A3A4∥A5A6,∴∠A=∠AA2A1=∠AA4A3=∠AA6A5,
∴a2=A3A4=AA3=1+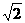 ,又∵∠A2A3A4=∠A4A5A6=90°,∠A2A4A3=∠A4A6A5,∴△A2A3A4∽△A4A5A6,
,又∵∠A2A3A4=∠A4A5A6=90°,∠A2A4A3=∠A4A6A5,∴△A2A3A4∽△A4A5A6,
∴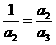 ,∴a3=
,∴a3=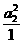 =(
=(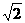 +1)2.
+1)2.
an=(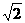 +1)n-1.
+1)n-1.
(3)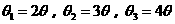
(4)由题意得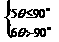 ,∴15°<
,∴15°<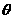 ≤18°.
≤18°.
2. (2011安徽芜湖,9,4分)如图,从边长为(a+4)cm的正方形纸片中剪去一个边长为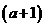 cm的正方形
cm的正方形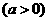 ,剩余部分沿虚线又剪拼成一个矩形(不重叠无缝隙),则矩形的面积为( ).
,剩余部分沿虚线又剪拼成一个矩形(不重叠无缝隙),则矩形的面积为( ).
A.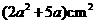 B.
B.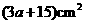 C.
C.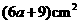 D.
D.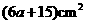
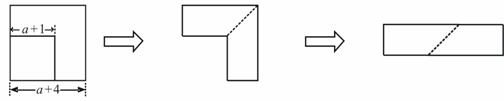
[答案]D
二 填空题
三 解答题
1. (2011广东广州市,8,3分)如图1所示,将矩形纸片先沿虚线AB按箭头方向向右对折,接着将对折后的纸片沿虚线CD向下对折,然后剪下一个小三角形,再将纸片打开,则打开后的展开图是( )
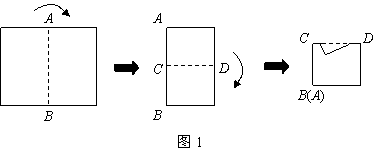
A. B. C. D.
[答案]D
14. (2011浙江省,20,8分)据媒体报道:某市四月份空气质量优良,高举全国榜首,青春中学九年级课外兴趣小组据此提出了“今年究竟能有多少天空气质量达到优良”的问题,他们高举国家环保总局所公布的空气质量级别表(见表1)以及市环保监测站提供的资料,从中随机抽取了今年1-4月份中30天空气综合污染指数,统计数据如下:
表I:空气质量级别表
|
空气污染 指数 |
0~50 |
51~100 |
101~150 |
151~200 |
201~250 |
251~300 |
大于300 |
|
空气质量级别 |
Ⅰ级(优) |
Ⅱ级(良) |
Ⅲ1(轻微污染) |
Ⅲ2(轻度污染) |
Ⅳ1(中度污染) |
Ⅳ2(中度重污染) |
Ⅴ(重度污染) |
空气综合污染指数
30,32,40,42,45,45,77,83,85,87,90,113,127,153,167
38,45,48,53,57,64,66,77,92,98,130,184,201,235,243
请根据空气质量级别表和抽查的空气综合污染指数,解答以下问题:
(1) 填写频率分布表中未完成的空格;
|
分组 |
频数统计 |
频数 |
频率 |
|
0~50 |
 |
|
0.30 |
|
51~100 |
 |
12 |
0.40 |
|
101~150 |
|
|
|
|
151~200 |
 |
3 |
0.10 |
|
201~250 |
 |
3 |
0.10 |
|
合计 |
30 |
30 |
1.00 |
(2) 写出统计数据中的中位数、众数;
(3)请根据抽样数据,估计该市今年(按360天计算)空气质量是优良(包括Ⅰ、Ⅱ级)的天数.
[答案](1)
|
分组 |
频数统计 |
频数 |
频率 |
|
0~50 |
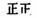 |
9 |
0.30 |
|
51~100 |
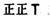 |
12 |
0.40 |
|
101~150 |
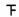 |
3 |
0.10 |
|
151~200 |
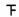 |
3 |
0.10 |
|
201~250 |
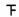 |
3 |
0.10 |
|
合计 |
30 |
30 |
1.00 |
(2) 中位数是 80 、众数是 45 。
(3) ∵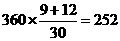
∴空气质量优良(包括Ⅰ、Ⅱ级)的天数是252天.
12. (2011广东省,18,7分)李老师为了解班里学生的作息时间,调查班上50名学生上学路上花费的时间,他发现学生所花时间都少于50分钟,然后将调查数据整理,作出如下频数分布直方图的一部分(每 组数据含最小值不含最大值).请根据该频数分布直方图,回答下列问题:
(1)此次调查的总体是什么?
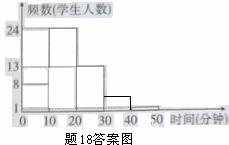
(2)补全频数分布直方图;
(3)该班学生上学路上花费时间在30分钟以上(含30分钟)的人数占全班人数的百分比是多少?
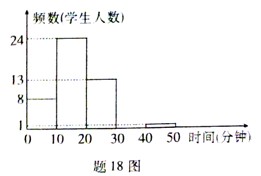
[解](1)此次调查的总体是:班上50名学生上学路上花费的时间的全体.
(2)补全图形,如图所示:
(3)该班学生上学路上花费时间在30分钟以上的人数有5人,总人数有50,
5÷50=0.1=10%
答:该班学生上学路上花费时间在30分钟以上的人数占全班人数的百分之10.
11. (2011山东聊城,19,8分)今年“世界水日”的主题是“城市用水:应对都市化挑战”.为了解城市居民用水量的情况,小亮随机抽查了阳光小区50户居民去年每户每月的用水量,将得到的数据整理并绘制了这50户居民去年每月总用水量的折线图和频数、频率分布表如下:
|
组 别
|
频 数
|
频 率 |
|
350<x≤400
|
1
|
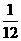
|
|
400<x≤450
|
1
|
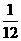
|
|
450<x≤500
|
2
|
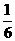 |
|
500<x≤550
|
a
|
b |
|
550<x≤600 |
c
|
d |
|
600<x≤650 |
1
|
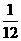 |
|
650<x≤700
|
2
|
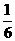
|
注:x表示50户居民月总用水量(m3)(1)表中的a=________;d=___________.
(2)这50户居民每月总用水量超过550m3的月份占全年月份的百分率是多少(精确到1%)?
(3)请根据折线统计图提供的数据,估计该小区去年每户居民平均月用水量是多少?
[答案](1)3,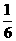 ;(2)这50户居民月总用水量超过550m3的月份有5个,占全年月份的百分率为(5÷12)×100%=42%
;(2)这50户居民月总用水量超过550m3的月份有5个,占全年月份的百分率为(5÷12)×100%=42%
(3)(378+641+456+543+550+667+693+600+574+526+423)÷50÷12=109m3
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com