
题目列表(包括答案和解析)
21、已知函数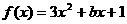 是偶函数,
是偶函数,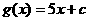 是奇函数,正数数列
是奇函数,正数数列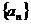 满足
满足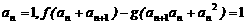
①
求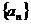 的通项公式;
的通项公式;
②若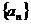 的前
的前 项和为
项和为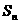 ,求
,求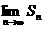 .
.
20.已知△OFQ的面积为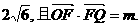
(1)设 正切值的取值范围;
正切值的取值范围;
(2)设以O为中心,F为焦点的双曲线经过点Q(如图),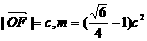 ,
,
当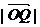 取得最小值时,求此双曲线的方程.
取得最小值时,求此双曲线的方程.
(3)设F1为(2)中所求双曲线的左焦点,若A、B分别为此双曲线渐近线l1、l2上的动
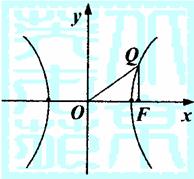 点,且2|AB|=5|F1F|,求线段AB的中点M的轨迹方程,并说明轨迹是什么曲线.
点,且2|AB|=5|F1F|,求线段AB的中点M的轨迹方程,并说明轨迹是什么曲线.
19.已知函数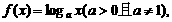 若数列:
若数列: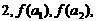 …,
…,
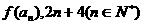 成等差数列.
成等差数列.
(1)求数列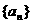 的通项
的通项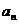 ;
;
(2)若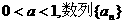 的前n项和为Sn,求
的前n项和为Sn,求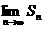 ;
;
(3)若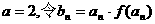 ,对任意
,对任意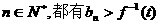 ,求实数t的取值范围.
,求实数t的取值范围.
18.已知函数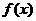 对任意实数p、q都满足
对任意实数p、q都满足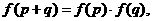
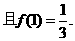
(1)当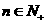 时,求
时,求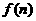 的表达式;
的表达式;
(2)设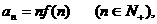 求证:
求证: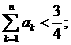
(3)设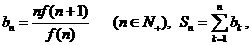 试比较
试比较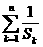 与6的大小.
与6的大小.
17. 已知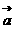 =(x,0),
=(x,0),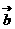 =(1,y),(
=(1,y),(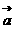 +
+
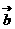 )
)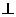 (
(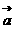 –
–
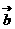 ).
).
(I)
求点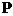 (x,y)的轨迹C的方程;
(x,y)的轨迹C的方程;
(II)
若直线L:y=kx+m(m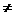 0)与曲线C交于A、B两点,D(0,–1),且有 |AD|=|BD|,试求m的取值范围.
0)与曲线C交于A、B两点,D(0,–1),且有 |AD|=|BD|,试求m的取值范围.
16.(14分)设f1(x)=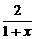 ,定义fn+1 (x)=f1[fn(x)],an=
,定义fn+1 (x)=f1[fn(x)],an=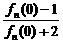 ,其中n∈N*.
,其中n∈N*.
(1) 求数列{an}的通项公式;
(2)若T2n=a1+2a2+3a3+…+2na2n,Qn=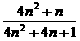 ,其中n∈N*,试比较9T2n与Qn的大小.
,其中n∈N*,试比较9T2n与Qn的大小.
15.(
12分)已知点H(-3,0),点P在y轴上,点Q在x轴的正半轴上,点M在直线PQ上,且满足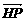 ·
·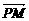 =0,
=0,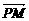 =-
=-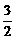
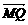 ,
,
(1)当点P在y轴上移动时,求点M的轨迹C;
(2)过点T(-1,0)作直线l与轨迹C交于A、B两点,若在x轴上存在一点E(x0,0),使得△ABE为等边三角形,求x0的值.
14.已知数列{an}各项均为正数,Sn为其前n项的和.对于任意的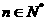 ,都有
,都有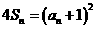 .
.
I、求数列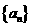 的通项公式.
的通项公式.
II、若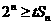 对于任意的
对于任意的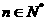 恒成立,求实数
恒成立,求实数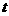 的最大值.
的最大值.
13.设关于x的方程2x2-tx-2=0的两根为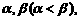 函数f(x)=
函数f(x)=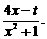
(1). 求f(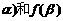 的值。
的值。
(2)。证明:f(x)在[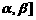 上是增函数。
上是增函数。
(3)。对任意正数x1、x2,求证: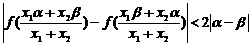
12.知函数f(x)=log3(x2-2mx+2m2+)的定义域为R (1)求实数m的取值集合M; (2)求证:对m∈M所确定的所有函数f(x)中,其函数值最小的一个是2,并求使函数值等于2的m的值和x的值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com