
题目列表(包括答案和解析)
5. 已知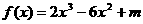 (m为常数)在
(m为常数)在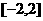 上有最大值3,那么此函数在
上有最大值3,那么此函数在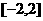 上的最小值为( )
上的最小值为( )
A. 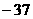 B.
B.
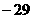 C.
C. 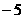 D.
D.
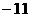
4. 若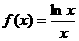 ,
,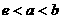 ,则( )
,则( )
A. 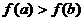 B.
B.
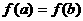
C. 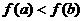 D.
D.
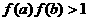
3. 已知曲线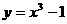 与曲线
与曲线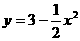 在
在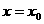 处的切线互相垂直,则
处的切线互相垂直,则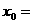 ( )
( )
A. 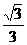 B.
B.
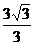 C.
C.
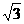 D.
D.
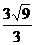
2. 点P在曲线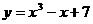 上移动,设点P处切线的倾斜角为
上移动,设点P处切线的倾斜角为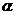 ,则角
,则角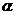 的取值范围是( )
的取值范围是( )
A. 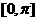 B.
B.
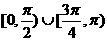
C. 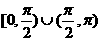 D.
D.
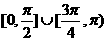
1. 函数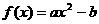 在区间
在区间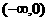 内是减函数,则
内是减函数,则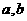 应满足( )
应满足( )
A. 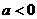 且b=0 B.
且b=0 B.
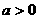 且
且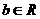
C. 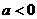 且
且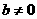 D.
D.
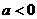 且
且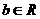
(15) 已知函数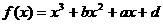 的图象过点P(0,2),且在点M
的图象过点P(0,2),且在点M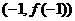 处的切线方程为
处的切线方程为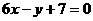 .
.
(Ⅰ)求函数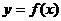 的解析式;
的解析式;
(Ⅱ)求函数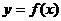 的单调区间.
的单调区间.
(16) 已知函数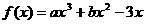 在
在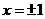 处取得极值.
处取得极值.
(Ⅰ)讨论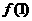 和
和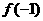 是函数
是函数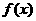 的极大值还是极小值;
的极大值还是极小值;
(Ⅱ)过点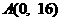 作曲线
作曲线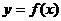 的切线,求此切线方程.
的切线,求此切线方程.
(17) 已知向量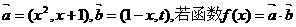 在区间(-1,1)上是增函数,求t的取值范围.
在区间(-1,1)上是增函数,求t的取值范围.
(18) 已知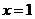 是函数
是函数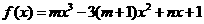 的一个极值点,其中
的一个极值点,其中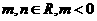 ,
,
(I)求 与
与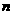 的关系式;
的关系式;
(II)求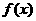 的单调区间;
的单调区间;
(III)(理科做)当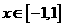 时,函数
时,函数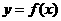 的图象上任意一点的切线斜率恒大于3
的图象上任意一点的切线斜率恒大于3 ,求
,求 的取值范围.
的取值范围.
(11)设f(x)= x|x|, 则f′( 0)= .
(12)函数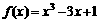 在闭区间[-3,0]上的最大值、最小值分别是
.
在闭区间[-3,0]上的最大值、最小值分别是
.
(13)若曲线y=h(x)在点P(a, h(a))处的切线方程为2x+y+1=0,则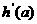 与0的大小关系是
与0的大小关系是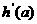 0
0
(14)过原点作曲线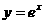 的切线,则切点的坐标为
,切线的斜率为 。
的切线,则切点的坐标为
,切线的斜率为 。
(1) 下列求导运算正确的是 ( )
A.(x+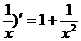 B.(log2x)′=
B.(log2x)′=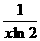
C.(3x)′=3xlog3e D. (x2cosx)′=-2xsinx
(2) 函数y=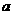 x2+1的图象与直线y=x相切,则
x2+1的图象与直线y=x相切,则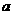 =
( )
=
( )
A. 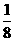 B.
B.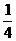 C.
C.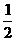 D.1
D.1
(3) 函数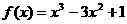 是减函数的区间为 ( )
是减函数的区间为 ( )
A.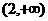 B.
B.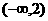 C.
C.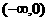 D.(0,2)
D.(0,2)
(4) 函数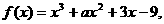 已知
已知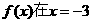 时取得极值,则
时取得极值,则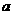 = ( )
= ( )
A.2 B.3 C.4 D.5
(5) 在函数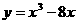 的图象上,其切线的倾斜角小于
的图象上,其切线的倾斜角小于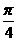 的点中,坐标为整数的点的个数是 ( )
的点中,坐标为整数的点的个数是 ( )
A.3 B.2 C.1 D.0
(6) 设f0(x) = sinx,f1(x)=f0′(x),f2(x)=f1′(x),…,fn+1(x) = fn′(x),n∈N,则f2005(x)= ( )
A.sinx B.-sinx C.cosx D.-cosx
(7) 已知函数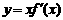 的图象如图所示(其中
的图象如图所示(其中 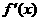 是函数
是函数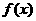 的导函数),下面四个图象中
的导函数),下面四个图象中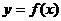 的图象大致是 ( )
的图象大致是 ( )
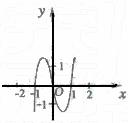
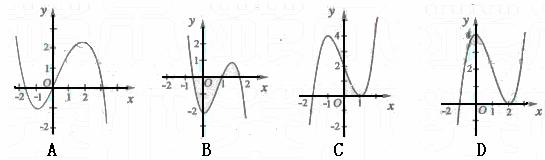
(8)设在[0, 1]上的函数f(x)的曲线连续, 且f′(x)>0, 则下列一定成立的是 ( )
A. f(0)<0 B. f(1)>0 C. f(1)> f(0) D. f(1)<f(0)
(9)设f(x)、g(x)分别是定义在R上的奇函数和偶函数,当x<0时,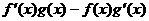 >0.且g(3)=0.则不等式f(x)g(x)<0的解集是 ( )
>0.且g(3)=0.则不等式f(x)g(x)<0的解集是 ( )
A. (-3,0)∪(3,+∞) B. (-3,0)∪(0, 3)
C. (-∞,- 3)∪(3,+∞) D. (-∞,- 3)∪(0, 3)
(10)若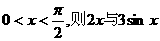 的大小关系
(
)
的大小关系
(
)
A.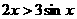 B.
B.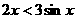 C.
C.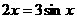 D.与x的取值有关
D.与x的取值有关
3.排列与组合的应用题
历届高考数学试题中,排列与组合部分的试题主要是应用问题。一般都附有某些限制条件;或是限定元素的选择,或是限定元素的位置,这些应用问题的内容和情景是多种多样的而解决它们的方法还是有规律可循的。常用的方法有:一般方法和特殊方法两种。
一般方法有:直接法和间接法
(1)在直接法中又分为两类,若问题可分为互斥各类,据加法原理,可用分类法;若问题考虑先后次序,据乘法原理,可用占位法。
(2)间接法一般用于当问题的反面简单明了,据A∪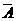 =I且A∩
=I且A∩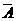 =Æ的原理,采用排除的方法来获得问题的解决。
=Æ的原理,采用排除的方法来获得问题的解决。
特殊方法:
(1)特元特位:优先考虑有特殊要求的元素或位置后,再去考虑其它元素或位置。
(2)捆绑法:某些元素必须在一起的排列,用“捆绑法”,紧密结合粘成小组,组内外分别排列。
(3)插空法:某些元素必须不在一起的分离排列用“插空法”,不需分离的站好实位,在空位上进行排列。
(4)其它方法。
例5.7人排成一行,分别求出符合下列要求的不同排法的种数。
(1)甲排中间;(2)甲不排两端;(3)甲,乙相邻;
(4)甲在乙的左边(不要求相邻);(5)甲,乙,丙连排;
(6)甲,乙,丙两两不相邻。
解:(1)甲排中间属“特元特位”,优先安置,只有一种站法,其余6人任意排列,故共有:1×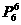 =720种不同排法。
=720种不同排法。
(2)甲不排两端,亦属于“特元特位”问题,优先安置甲在中间五个位置上任何一个位置则有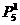 种,其余6人可任意排列有
种,其余6人可任意排列有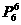 种,故共有
种,故共有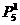 ·
·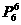 =3600种不同排法。
=3600种不同排法。
(3)甲、乙相邻,属于“捆绑法”,将甲、乙合为一个“元素”,连同其余5人共6个元素任意排列,再由甲、乙组内排列,故共有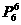 ·
·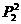 =1400种不同的排法。
=1400种不同的排法。
(4)甲在乙的左边。考虑在7人排成一行形成的所有排列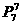 中:“甲在乙左边”与“甲在乙右边”的排法是一一对应的,在不要求相邻时,各占所有排列的一半,故甲在乙的左边的不同排法共有
中:“甲在乙左边”与“甲在乙右边”的排法是一一对应的,在不要求相邻时,各占所有排列的一半,故甲在乙的左边的不同排法共有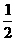
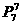 =2520种。
=2520种。
(5)甲、乙、丙连排,亦属于某些元素必须在一起的排列,利用“捆绑法”,先将甲、乙、丙合为一个“元素”,连同其余4人共5个“元素”任意排列,现由甲、乙、丙交换位置,故共有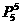 ·
·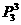 =720种不同排法。
=720种不同排法。
(6)甲、乙、丙两两不相邻,属于某些元素必须不在一起的分离排列,用“插空法”,先将甲、乙、丙外的4人排成一行,形成左、右及每两人之间的五个“空”。再将甲、乙、丙插入其中的三个“空”,故共有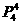 ·
·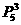 =1440种不同的排法。
=1440种不同的排法。
例6.用0,1,2,3,4,5这六个数字组成无重复数字的五位数,分别求出下列各类数的个数:
(1)奇数;(2)5的倍数;(3)比20300大的数;
(4)不含数字0,且1,2不相邻的数。
解:(1)奇数:要得到一个5位数的奇数,分成3步,第一步考虑个位必须是奇数,从1,3,5中选出一个数排列个位的位置上有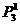 种;第二步考虑首位不能是0,从余下的不是0的4个数字中任选一个排在首位上有
种;第二步考虑首位不能是0,从余下的不是0的4个数字中任选一个排在首位上有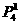 种;第三步:从余下的4个数字中任选3个排在中间的3个
种;第三步:从余下的4个数字中任选3个排在中间的3个
数的位置上,由乘法原理共有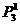
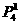
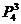 =388(个)。
=388(个)。
(2)5的倍数:按0作不作个位来分类
第一类:0作个位,则有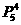 =120。
=120。
第二类:0不作个位即5作个位,则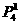
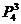 =96。
=96。
则共有这样的数为: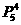 +
+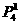
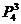 =216(个)。
=216(个)。
(3)比20300大的数的五位数可分为三类:
第一类:3xxxx, 4xxxx, 5xxxx有3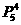 个;
个;
第二类:21xxx, 23xxx, 24xxx, 25xxx, 的4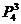 个;
个;
第三类:203xx, 204xx, 205xx, 有3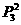 个,因此,比20300大的五位数共有:
个,因此,比20300大的五位数共有:
3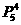 +4
+4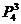 +3
+3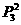 =474(个)。
=474(个)。
(4)不含数字0且1,2不相邻的数:分两步完成,第一步将3,4,5三个数字排成一行;第二步将1和2插入四个“空”中的两个位置,故共有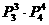 =72个不含数字0,且1和2不相邻的五位数。
=72个不含数字0,且1和2不相邻的五位数。
例7.直线与圆相离,直线上六点A1,A2,A3,A4,A5,A6,圆上四点B1,B2,B3,B4,任两点连成直线,问所得直线最多几条?最少几条?
解:所得直线最多时,即为任意三点都不共线可分为三类:第一类为已知直线上与圆上各取一点连线的直线条数为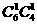 =24;第二类为圆上任取两点所得的直线条数为
=24;第二类为圆上任取两点所得的直线条数为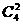 =6;第三类为已知直线为1条,则直线最多的条数为N1=
=6;第三类为已知直线为1条,则直线最多的条数为N1=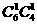 +
+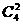 +1=31(条)。
+1=31(条)。
所得直线最少时,即重合的直线最多,用排除法减去重合的字数较为方便,而重合的直线即是由圆上取两点连成的直线,排除重复,便是直线最少条数:
N2=N1-2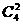 =31-12=19(条)。
=31-12=19(条)。
2.排列数与组合数的两个公式
排列数与组合数公式各有两种形式,一是连乘积的形式,这种形式主要用于计算;二是阶乘的形式,这种形式主要用于化简与证明。
连乘积的形式 阶乘形式
Pnm=n(n-1)(n-2)……(n-m+1) =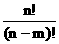
Cnm=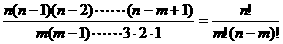
例3.求证:Pnm+mPnm-1=Pn+1m
证明:左边=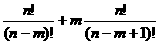
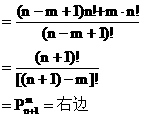
∴ 等式成立。
评述:这是一个排列数等式的证明问题,选用阶乘之商的形式,并利用阶乘的性质。
n!(n+1)=(n+1)!.可使变形过程得以简化。
例4.解方程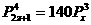 .
.
解:原方程可化为:
Û 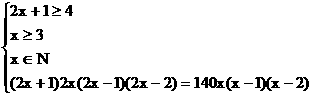
Û 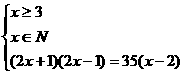
Û 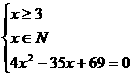 解得x=3.
解得x=3.
评述:解由排列数与组合数形式给出的方程时,在脱掉排列数与组合数的符号时,要注意把排列数与组合数定义中的取出元素与被取元素之间的关系以及它们都属自然数的这重要限定写在脱掉符号之前。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com