
题目列表(包括答案和解析)
6.设0<x<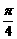 ,下列关系中正确的是( )
,下列关系中正确的是( )
A、sin(sinx)<sinx<sin(tgx) B、sin(sinx)<sin(tgx)<sinx
C、sin(tgx)<sinx<sin(sinx) D、sinx<sin(tgx)<sin(sinx)
5.已知函数y=cos(sinx),下列结论中正确的是( )
A、它的定义域是[-1,1] B、它是奇函数;
C、它的值域是[0, 1] D、它是周期为p的函数
4.函数y=2sin(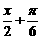 )在[p,2p]上的最小值是( )
)在[p,2p]上的最小值是( )
A、2 B、1 C、-1 D、-2
3.若p<q<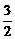 p, 则
p, 则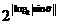 等于( )
等于( )
A、sin(q-p) B、-sinq C、cos(p-q) D、-cscq
2.在下列表示中正确的是( )
A、终边在y轴上的角的集合是{a|a=2kp+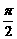 , kÎZ}
, kÎZ}
B、终边在y=x的直线上的角的集合是{a|a=kp+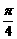 , kÎZ}
, kÎZ}
C、与(-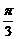 )的终边相同的角的集合是{a|a=kp-
)的终边相同的角的集合是{a|a=kp-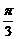 , kÎZ}
, kÎZ}
D、终边在y=-x的直线上的角的集合是{a|a=2kp-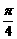 , kÎZ}
, kÎZ}
例1.(1)已知-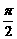 <a<b<
<a<b<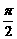 , 求a+b与a-b的范围。
, 求a+b与a-b的范围。
(2)已知a的终边在第二象限,确定p-a所在象限。
解:(1)∵-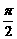 <a<b<
<a<b<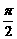 , ∴-p<a+b<p,-p<a-b<0.
, ∴-p<a+b<p,-p<a-b<0.
(2)有两种思路:其一是先把a的终边关于x轴对称放到-a的终边(在第三象限),再将-a的终边按逆时方向旋转p放到p-a的终边即-a的终边的反向延长线,此时p-a的终边也在第二象限。
思路2:是先把a的终边(第二象限)按顺时针方向旋转p,得到a+(-p)(第四象限),再将它关于x轴对称得到-(a-p)=p-a的终边,此时也在第一象限。
例2.若A={x|x=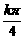 , kÎZ},
B={x|x=
, kÎZ},
B={x|x=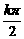 +
+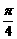 , kÎZ}, 则A _____B。
, kÎZ}, 则A _____B。
解:由B中的x=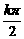 +
+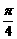 =
=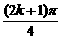 可视为
可视为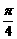 的奇数倍所构成的集合。
的奇数倍所构成的集合。
而A中的x=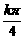 是
是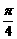 的所有奇数倍,因此AÉB。
的所有奇数倍,因此AÉB。
例3.设0<q<2p, 问5q与角q终边相同,求q。
解:由已知 5q=2kp+q, kÎZ, 有q=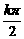 ,
,
∵ 0<q<2p, ∴k=1时,q=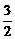 ;k=2时,q=p;k=3时,q=
;k=2时,q=p;k=3时,q=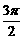 .
.
例4.若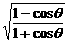 =ctgq-cscq,求q取值范围。
=ctgq-cscq,求q取值范围。
解:先看一看右边=ctgq-cscq=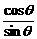 -
-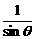 =
=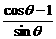 ,这样就决定了左边的变形方向。
,这样就决定了左边的变形方向。
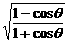 =
=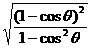 =
=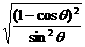 ,
,
∵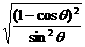 =
=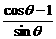 , ∴
, ∴ 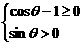 Þ
Þ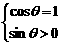 Þq无解,
Þq无解,
∴ 不存在这样的q使所给等式成立。
例5.已知sin(p-a)-cos(p+a)=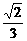 ,
, 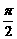 <a<p.
<a<p.
求:(1)sina-cosa的值 (2)sin3(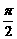 +a)+cos3(
+a)+cos3(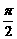 +a)的值
+a)的值
解:(1)由已知,得sina+cosa=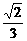 ,平方得:1+2sinacosa=
,平方得:1+2sinacosa=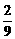 ,
,
∴ 2sinacosa=-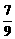 ,
,
∵ 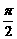 <a<p,
<a<p,
∴ sina-cosa=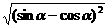 =
=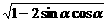 =
=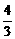 .
.
(2)sin3(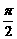 +a)+cos3(
+a)+cos3(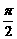 +a)=cos3a-sin3a
+a)=cos3a-sin3a
=(cosa-sina)(cos2a+sinacosa+sin2a)
=-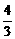 (1-
(1-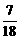 )
)
=-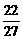 .
.
例6.已知sin(a-p)=2cos(a-2p),求下列三角函数的值:
(1)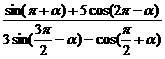 (2)1+cos2a-
(2)1+cos2a-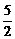 sin2a.
sin2a.
解:由已知:-sina=2cosa,有 tga=-2, 则
(1)原式=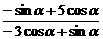 =
=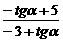 =-
=-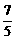 。
。
(2)1+cos2a-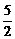 sin2a
sin2a
=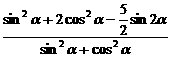 =
=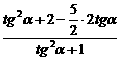
=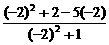 =
=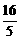 .
.
评述:对于形如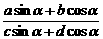 为关于sina与cosa的一次分式齐次式,处理的方法,就是将分子与分母同除以cosa,即可化为只含tga的式子。而对于1+cos2a-
为关于sina与cosa的一次分式齐次式,处理的方法,就是将分子与分母同除以cosa,即可化为只含tga的式子。而对于1+cos2a-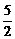 sin2a属于关于sina与cosa的二次齐次式。即sin2a+2cos2a-5sinacosa. 此时若能将分母的“1”用sin2a+cos2a表示的话,这样就构成了关于sina与cosa的二次分式齐次式,分子分母同除以cos2a即可化为只含有tga的分式形式。
sin2a属于关于sina与cosa的二次齐次式。即sin2a+2cos2a-5sinacosa. 此时若能将分母的“1”用sin2a+cos2a表示的话,这样就构成了关于sina与cosa的二次分式齐次式,分子分母同除以cos2a即可化为只含有tga的分式形式。
例7.求函数y=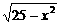 +logsinx(2sinx-1)的定义域。
+logsinx(2sinx-1)的定义域。
解:使函数有意义的不等式为: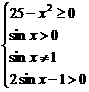 Þ
Þ 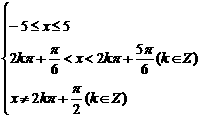
将上面的每个不等式的范围在数轴上表示出来,然后,取公共部分,由于xÎ[-5,5],故下面的不等式的范围只取落入[-5,5]之内的值,即

∴因此函数的定义域为:
[-5,-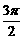 )∪(-
)∪(-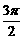 ,-
,-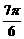 )∪(
)∪(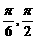 )∪(
)∪(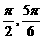 )。
)。
例8.求证: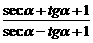 =
=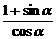 .
.
证法一(左边化弦后再证等价命题)
左边=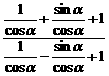 =
=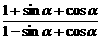
要证 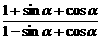 =
=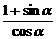
只需证:(1+sina+cosa)cosa=(1-sina+cosa)(1+sina)
左边=cosa+sinacosa+cos2a
右边=1-sin2a+cosa+cosasina=cos2a+cosa+sinacosa
∵左边=右边,∴原等式成立。
或证等价命题: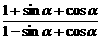 -
-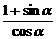 =0
=0
证法二(利用化“1”的技巧)
左边=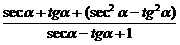
=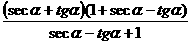 =seca+tga=
=seca+tga=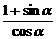 =右边。
=右边。
证法三(利用同角关系及比例的性质)
由公式 sec2a-tg2a=1
Þ(seca-tga)(seca+tga)=1
Þ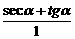 =
=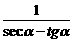 .
.
由等比定理有: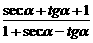 =seca+tga=
=seca+tga=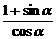 .
.
证法四(利用三角函数定义)
证seca=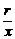 , tga=
, tga=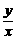 , sina=
, sina=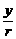 , cosa=
, cosa=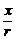 .
.
然后代入所证等式的两边,再证是等价命题。
其证明过程同学自己尝试一下。
评述:证明三角恒等式的实质,就是逐步消除等号两边结构差异的过程,而“消除差异”的理论依据除了必要三角公式以外,还需要有下列等式的性质:
(1)若A=B,B=C则A=C(传递性)
(2)A=BÛA-B=0
(3)A=BÛ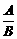 =1 (B¹0)
=1 (B¹0)
(4)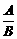 =
=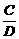 Û AD=BC
(BD¹0)
Û AD=BC
(BD¹0)
(5)比例:一些性质,如等比定理:
若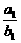 =
=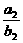 =……=
=……=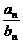 ,则
,则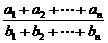 =
=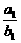 =
=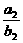 =……=
=……=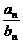 。
。
1.如果q是第二象限角,则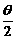 所在的象限是( )
所在的象限是( )
A、第一象限 B、第一或第三象限 C、第二象限 D、第二或第四象限
3.诱导公式
总共9组共36个公式,记忆口决为“奇变偶不变,符号看象限”,并弄清口决中的字词含义,并根据结构总结使用功能。
“奇变”是指所涉及的轴上角为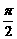 的奇数倍时(包括4组:
的奇数倍时(包括4组: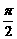 ±a,
±a,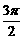 ±a)函数名称变为原来函数的余函数;其主要功能在于:当需要改变函数名称时,比如:由于“和差化积”公式都是同名函数的和差。使用时,对于不同名的函数先化为同名函数,又如:复数化三角形式,有时也需要改变函数名称,如:sina-icosa=cos(
±a)函数名称变为原来函数的余函数;其主要功能在于:当需要改变函数名称时,比如:由于“和差化积”公式都是同名函数的和差。使用时,对于不同名的函数先化为同名函数,又如:复数化三角形式,有时也需要改变函数名称,如:sina-icosa=cos(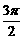 +a)+isin(
+a)+isin(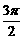 +a)。
+a)。
“偶不变”是指所涉及的轴上角为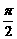 的偶数倍时(包括5组:2kp+a, p±a, 2p-a, -a), 函数名称不变,其主要功能在于:求任意角的三角函数值,化简及某些证明问题。
的偶数倍时(包括5组:2kp+a, p±a, 2p-a, -a), 函数名称不变,其主要功能在于:求任意角的三角函数值,化简及某些证明问题。
2.任意角的三角函数定义
任意角的6个三角函数定义的本质是给角这个几何量以代数表达。借助直角坐标系这个工具,把角放进直角坐标系中完成的。由任意角的三角函数定义直接可以得到:
(1)三角函数的定义域
(2)三角函数值在四个象限中的符号
(3)同角三角函数的关系
(4)单位圆中的三角函数线:要充分利用三角函数线在记忆三角函数性质与公式以及解决三角函数问题中的作用。
1.角的概念
(1)角的定义及正角,负角与零角
(2)象限角与轴上角的表达
(3)终边相同的角
(4)角度制
(5)弧度制
题,如果两题都做,以第14题的得分为最后得分),满分20分.
11.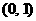 . 12.
. 12. 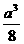 . 13.(Ⅰ)
. 13.(Ⅰ)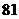 ; (Ⅱ)
; (Ⅱ) . 14.
. 14.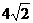 . 15.
. 15.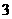 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com