
题目列表(包括答案和解析)
1.加法原理和乘法原理
两个原理是理解排列与组合的概念,推导排列数及组合数公式;分析和解决排列与组合的应用问题的基本原则和依据;完成一件事共有多少种不同方法,这是两个原理所要回答的共同问题。而两者的区别在于完成一件事可分几类办法和需要分几个步骤。
例1.书架上放有3本不同的数学书,5本不同的语文书,6本不同的英语书。
(1)若从这些书中任取一本,有多少种不同的取法? (2)若从这些书中取数学书、语文书、英语书各一本,有多少种不同的取法?
(3)若从这些书中取不同的科目的书两本,有多少种不同的取法。
解:(1)由于从书架上任取一本书,就可以完成这件事,故应分类,由于有3种书,则分为3类然后依据加法原理,得到的取法种数是:3+5+6=14种。
(2)由于从书架上任取数学书、语文书、英语书各1本,需要分成3个步骤完成,据乘法原理,得到不同的取法种数是:3×5×6=90(种)。
(3)由于从书架上任取不同科目的书两本,可以有3类情况(数语各1本,数英各1本,语英各1本)而在每一类情况中又需分2个步骤才能完成。故应依据加法与乘法两个原理计算出共得到的不同的取法种数是:3×5+3×6+5×6=63(种)。
例2.已知两个集合A={1,2,3},B={a,b,c,d},从A到B建立映射,问可建立多少个不同的映射?
分析:首先应明确本题中的“这件事是指映射,何谓映射?即对A中的每一个元素,在B中都有唯一的元素与之对应。”
因A中有3个元素,则必须将这3个元素都在B中找到家,这件事才完成。因此,应分3个步骤,当这三个步骤全进行完,一个映射就被建立了,据乘法原理,共可建立不同的映射数目为:5×5×5=53(种)。
22.已知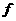 (x)在
(x)在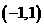 上有定义,
上有定义,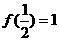 ,且满足
,且满足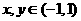 时有
时有
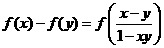 ,对数列
,对数列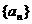 满足
满足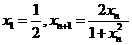
(1)证明: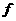 (x)在(-1,1)上为奇函数;
(x)在(-1,1)上为奇函数;
(2)求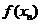 的表达式;
的表达式;
(3)是否存在自然数m,使得对于任意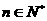 ,有
,有 成立?若存在,求出m的最小值.
成立?若存在,求出m的最小值.
21.已知数列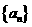 的首项
的首项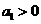 ,公比
,公比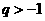 且
且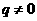 的等比数列,设数列
的等比数列,设数列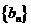 的通项
的通项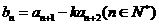 ,数列
,数列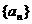 ,
,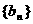 的前n项之和分别为
的前n项之和分别为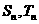 ,如果存在常数k,使得对所有的适合条件的两个数列,均有
,如果存在常数k,使得对所有的适合条件的两个数列,均有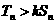 对一切
对一切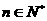 都成立,试求实数k的取值范围。
都成立,试求实数k的取值范围。
20.用分期付款方式购买家用电器一件,价格为1150元,购买当天先付150元,以后每月这一天都交付50元,并加付欠款的利息,月利率为1%,若交付150元后的第一个月开始算分期付款的第一个月,问分期付款的第十个月该交付多少钱?全部货款付清后,买这件家电实际花了多少钱?
19.已知数列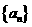 是等差数列,其前项和为
是等差数列,其前项和为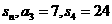 。
。
(1)求数列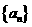 的通项公式
的通项公式
(2)设p,q是正整数,且p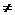 q,证明
q,证明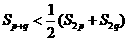
18.数列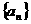 满足条件
满足条件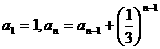
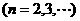
(1)求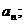 (2)求
(2)求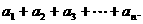
17.设数列{a n}的前n项和为S n,已知an=5S n-3 (n∈N+),{bn}是{a n}的奇数项构成的数列,求数列{bn} 的通项公式.
16.依次写出数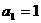 ,
,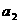 ,
,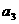 ,…法则如下:如果
,…法则如下:如果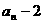 为自然数且未写出过,则写
为自然数且未写出过,则写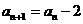 ,否则就写
,否则就写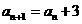 ,那么
,那么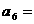
15.已知等差数列有一性质:若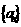 是等差数列.则通项为
是等差数列.则通项为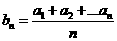 的数列
的数列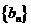 也是等差数列,类似上述命题,相应的等比数列有性质:若
也是等差数列,类似上述命题,相应的等比数列有性质:若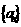 是等比数列
是等比数列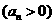 ,则通项为
,则通项为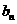 =_____________的数列
=_____________的数列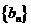 也是等比数列
也是等比数列
14. 设数列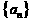 的前
的前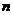 项和为
项和为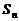 (
(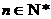 ). 关于数列
). 关于数列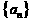 有下列三个命题:
有下列三个命题:
(1)若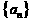 既是等差数列又是等比数列,则
既是等差数列又是等比数列,则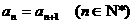 ;
;
(2)若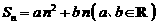 ,则
,则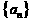 是等差数列;
是等差数列;
(3)若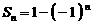 ,则
,则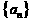 是等比数列.
是等比数列.
这些命题中,真命题的序号是 .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com