
题目列表(包括答案和解析)
3.三角形的面积公式:
(1)△=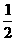 aha=
aha=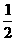 bhb=
bhb=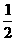 chc(ha、hb、hc分别表示a、b、c上的高);
chc(ha、hb、hc分别表示a、b、c上的高);
(2)△=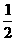 absinC=
absinC=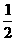 bcsinA=
bcsinA=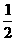 acsinB;
acsinB;
(3)△=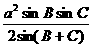 =
=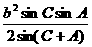 =
=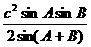 ;
;
(4)△=2R2sinAsinBsinC。(R为外接圆半径)
(5)△=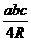 ;
;
(6)△=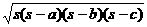 ;
;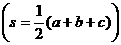 ;
;
(7)△=r·s。
2.斜三角形中各元素间的关系:
如图6-29,在△ABC中,A、B、C为其内角,a、b、c分别表示A、B、C的对边。
(1)三角形内角和:A+B+C=π。
(2)正弦定理:在一个三角形中,各边和它所对角的正弦的比相等
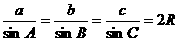 。
。
(R为外接圆半径)
(3)余弦定理:三角形任何一边的平方等于其他两边平方的和减去这两边与它们夹角的余弦的积的两倍
a2=b2+c2-2bccosA;b2=c2+a2-2cacosB;c2=a2+b2-2abcosC。
1.直角三角形中各元素间的关系:
如图,在△ABC中,C=90°,AB=c,AC=b,BC=a。
(1)三边之间的关系:a2+b2=c2。(勾股定理)
(2)锐角之间的关系:A+B=90°;
(3)边角之间的关系:(锐角三角函数定义)
sinA=cosB=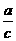 ,cosA=sinB=
,cosA=sinB=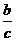 ,tanA=
,tanA=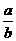 。
。
对本讲内容的考察主要涉及三角形的边角转化、三角形形状的判断、三角形内三角函数的求值以及三角恒等式的证明问题,立体几何体的空间角以及解析几何中的有关角等问题。今后高考的命题会以正弦定理、余弦定理为知识框架,以三角形为主要依托,结合实际应用问题考察正弦定理、余弦定理及应用。题型一般为选择题、填空题,也可能是中、难度的解答题
(1)通过对任意三角形边长和角度关系的探索,掌握正弦定理、余弦定理,并能解决一些简单的三角形度量问题;
(2)能够运用正弦定理、余弦定理等知识和方法解决一些与测量和几何计算有关的实际问题。
4.画水平放置的多边形的直观图的关键是确定多边形顶点的位置,因为多边形顶点的位置一旦确定,依次连结这些顶点就可画出多边形来,因此平面多边形水平放置时,直观图的画法可以归结为确定点的位置的画法
3.
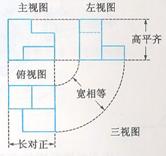 三视图画法规则
三视图画法规则
高平齐:主视图与左视图的高要保持平齐
长对正:主视图与俯视图的长应对正
宽相等:俯视图与左视图的宽度应相等
2.一些特殊棱柱、棱锥、棱台的概念和主要性质
|
名称 |
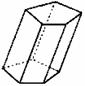
棱柱 |
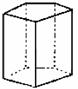
直棱柱 |
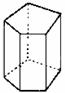
正棱柱 |
|
图 形 |
 |
 |
 |
|
定 义 |
有两个面互相平行,而其余每相邻两个面的交线都互相平行的多面体 |
侧棱垂直于底面的棱柱 |
底面是正多边形的直棱柱 |
|
侧棱 |
平行且相等 |
平行且相等 |
平行且相等 |
|
侧面的形状 |
平行四边形 |
矩形 |
全等的矩形 |
|
对角面的形状 |
平行四边形 |
矩形 |
矩形 |
|
平行于底面的截面的形状 |
与底面全等的多边形 |
与底面全等的多边形 |
与底面全等的正多边形 |
|
名称 |
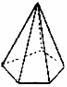
棱锥 |
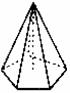
正棱锥 |
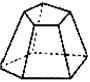
棱台 |
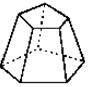
正棱台 |
|
图形 |
 |
 |
 |
 |
|
定义 |
有一个面是多边形,其余各面是有一个公共顶点的三角形的多面体 |
底面是正多边形,且顶点在底面的射影是底面的射影是底面和截面之间的部分 |
用一个平行于棱锥底面的平面去截棱锥,底面和截面之间的部分 |
由正棱锥截得的棱台 |
|
侧棱 |
相交于一点但不一定相等 |
相交于一点且相等 |
延长线交于一点 |
相等且延长线交于一点 |
|
侧面的形状 |
三角形 |
全等的等腰三角形 |
梯形 |
全等的等腰梯形 |
|
对角面的形状 |
三角形 |
等腰三角形 |
梯形 |
等腰梯形 |
|
平行于底的截面形状 |
与底面相似的多边形 |
与底面相似的正多边形 |
与底面相似的多边形 |
与底面相似的正多边形 |
|
其他性质 |
|
高过底面中心;侧棱与底面、侧面与底面、相邻两侧面所成角都相等 |
|
两底中心连线即高;侧棱与底面、侧面与底面、相邻两侧面所成角都相等 |
几种特殊四棱柱的特殊性质
|
名称 |
特殊性质 |
|
平行六面体 |
底面和侧面都是平行四边行;四条对角线交于一点,且被该点平分 |
|
直平行六面体 |
侧棱垂直于底面,各侧面都是矩形;四条对角线交于一点,且被该点平分 |
|
长方体 |
底面和侧面都是矩形;四条对角线相等,交于一点,且被该点平分 |
|
正方体 |
棱长都相等,各面都是正方形四条对角线相等,交于一点,且被该点平分 |
1.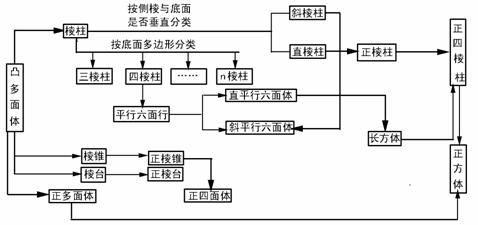 几种常凸多面体间的关系
几种常凸多面体间的关系
题型1:空间几何体的构造
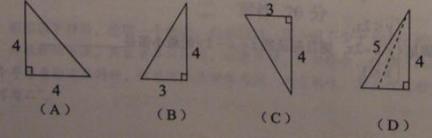 例1.9,如图,已知三棱锥的底面是直角三角形,直角边长分别为3和4,过直角顶点的侧棱长为4,且垂直于底面,该三棱锥的主视图是( )
例1.9,如图,已知三棱锥的底面是直角三角形,直角边长分别为3和4,过直角顶点的侧棱长为4,且垂直于底面,该三棱锥的主视图是( )
答案 B
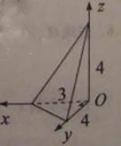
2.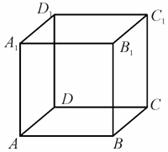 (2009湖南卷理)正方体ABCD-
(2009湖南卷理)正方体ABCD-
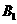

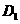 的棱上到异面直线AB,C
的棱上到异面直线AB,C 的距离相等的点的个数为(C)
的距离相等的点的个数为(C)
A.2 B.3 C. 4 D. 5
[答案]:C
[解析]解析如图示,则BC中点,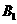 点,
点,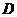 点,
点,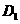 点分别到两异面直线的距离相等。即满足条件的点有四个,故选C项
点分别到两异面直线的距离相等。即满足条件的点有四个,故选C项
(3)正方体ABCD_A1B1C1D1的棱长为2,点M是BC的中点,点P是平面ABCD内的一个动点,且满足PM=2,P到直线A1D1的距离为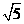 ,则点P的轨迹是[ ]
,则点P的轨迹是[ ]
A.圆 B.双曲线 C.两个点 D.直线
解析: 点P到A1D1的距离为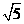 ,则点P到AD的距离为1,满足此条件的P的轨迹是到直线AD的距离为1的两条平行直线,
,则点P到AD的距离为1,满足此条件的P的轨迹是到直线AD的距离为1的两条平行直线,
又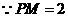 ,
, 满足此条件的P的轨迹是以M为圆心,半径为2的圆,这两种轨迹只有两个交点.
满足此条件的P的轨迹是以M为圆心,半径为2的圆,这两种轨迹只有两个交点.
故点P的轨迹是两个点。选项为C。
点评:该题考察空间内平面轨迹的形成过程,考察了空间想象能力。
 例2.(07江苏9)
例2.(07江苏9)
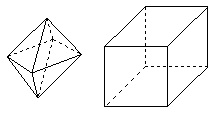
两相同的正四棱锥组成如图1所示的几何体,可放棱长为1的正方体内,使正四棱锥的底面ABCD与正方体的某一个平面平行,且各顶点均在正方体的面上,则这样的几何体体积的可能值有( )
A.1个 B.2个 C.3个 D.无穷多个
解析:由于两个正四棱锥相同,所以所求几何体的中心在正四棱锥底面正方形ABCD中心,有对称性知正四棱锥的高为正方体棱长的一半,影响几何体体积的只能是正四棱锥底面正方形ABCD的面积,问题转化为边长为1的正方形的内接正方形有多少种,所以选D。
点评:本题主要考查空间想象能力,以及正四棱锥的体积。正方体是大家熟悉的几何体,它的一些内接或外接图形需要一定的空间想象能力,要学会将空间问题向平面问题转化。
题型2:空间几何体的定义
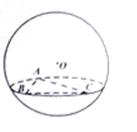 例3.(2009四川卷理)如图,在半径为3的面上有
例3.(2009四川卷理)如图,在半径为3的面上有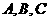 三点,
三点, ,球心
,球心 到平面
到平面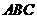 的距离是
的距离是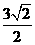 ,则
,则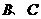 两点的球面距离是
两点的球面距离是
A.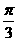 B.
B.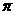 C.
C.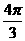 D.
D.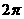
[考点定位]本小题考查球的截面圆性质、球面距,基础题。(同文9)
解析:由知截面圆的半径
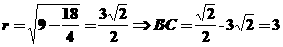 ,故
,故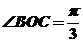 ,所以
,所以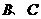 两点的球面距离为
两点的球面距离为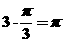 ,故选择B。
,故选择B。
解析2:过球心 作平面
作平面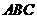 的垂线交平面与
的垂线交平面与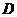 ,
,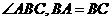 ,则
,则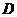 在直线
在直线 上,由于
上,由于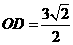 ,
,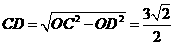 ,所以
,所以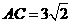 ,由
,由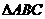 为等腰直角三角形可得
为等腰直角三角形可得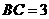 ,所以
,所以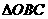 为等边三角形,则
为等边三角形,则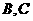 两点的球面距离是
两点的球面距离是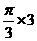 。
。
例4.(2009浙江卷文)设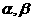 是两个不同的平面,
是两个不同的平面,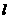 是一条直线,以下命题正确的是( )
是一条直线,以下命题正确的是( )
A.若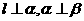 ,则
,则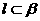 B.若
B.若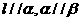 ,则
,则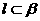
C.若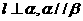 ,则
,则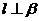 D.若
D.若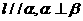 ,则
,则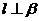
[命题意图]此题主要考查立体几何的线面、面面的位置关系,通过对平行和垂直的考查,充分调动了立体几何中的基本元素关系.
[解析]对于A、B、D均可能出现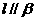 ,而对于C是正确的
,而对于C是正确的
点评:对于空间几何体的定义要有深刻的认识,掌握它们并能判断它们的性质。
题型3:空间几何体中的想象能力
例5.(2009北京卷理)(本小题共14分)
如图,在三棱锥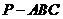 中,
中,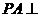 底面
底面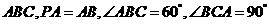 ,
,
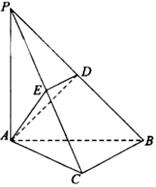 点
点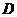 ,
,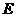 分别在棱
分别在棱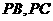 上,且
上,且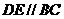
(Ⅰ)求证: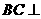 平面
平面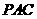 ;
;
(Ⅱ)当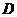 为
为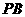 的中点时,求
的中点时,求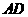 与平面
与平面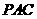 所成的角的大小;
所成的角的大小;
(Ⅲ)是否存在点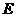 使得二面角
使得二面角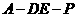 为直二面角?并说明理由.
为直二面角?并说明理由.
[解法1]本题主要考查直线和平面垂直、直线与平面所成的角、二面角等基础知识,考查空间想象能力、运算能力和推理论证能力.
(Ⅰ)∵PA⊥底面ABC,∴PA⊥BC.
又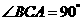 ,∴AC⊥BC.
,∴AC⊥BC.
∴BC⊥平面PAC.
(Ⅱ)∵D为PB的中点,DE//BC,
∴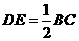 ,
,
又由(Ⅰ)知,BC⊥平面PAC,
∴DE⊥平面PAC,垂足为点E.
∴∠DAE是AD与平面PAC所成的角,
∵PA⊥底面ABC,∴PA⊥AB,又PA=AB,
∴△ABP为等腰直角三角形,∴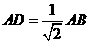 ,
,
∴在Rt△ABC中,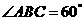 ,∴
,∴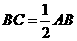 .
.
∴在Rt△ADE中,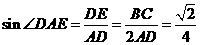 ,
,
∴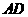 与平面
与平面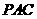 所成的角的大小
所成的角的大小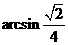 .
.
(Ⅲ)∵AE//BC,又由(Ⅰ)知,BC⊥平面PAC,∴DE⊥平面PAC,
又∵AE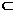 平面PAC,PE
平面PAC,PE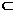 平面PAC,∴DE⊥AE,DE⊥PE,
平面PAC,∴DE⊥AE,DE⊥PE,
∴∠AEP为二面角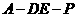 的平面角,
的平面角,
∵PA⊥底面ABC,∴PA⊥AC,∴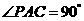 .
.
∴在棱PC上存在一点E,使得AE⊥PC,这时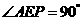 ,
,
故存在点E使得二面角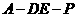 是直二面角.
是直二面角.
[解法2]如图,以A为原煤点建立空间直角坐标系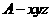 ,
,
设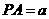 ,由已知可得
,由已知可得
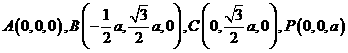 .
.
(Ⅰ)∵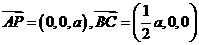 ,
,
∴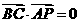 ,∴BC⊥AP.
,∴BC⊥AP.
又∵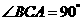 ,∴BC⊥AC,∴BC⊥平面PAC.
,∴BC⊥AC,∴BC⊥平面PAC.
(Ⅱ)∵D为PB的中点,DE//BC,∴E为PC的中点,
∴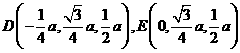 ,
,
∴又由(Ⅰ)知,BC⊥平面PAC,∴∴DE⊥平面PAC,垂足为点E.
∴∠DAE是AD与平面PAC所成的角,
∵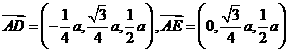 ,
,
∴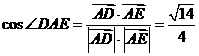 .
.
∴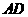 与平面
与平面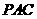 所成的角的大小
所成的角的大小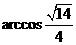 .
.
(Ⅲ)同解法1.
例6.(2009全国卷Ⅱ文)(本小题满分12分
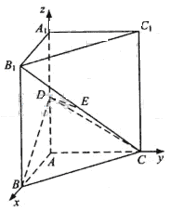
如图,直三棱柱ABC-A1B1C1中,AB⊥AC,D、E分别为AA1、B1C的中点,DE⊥平面BCC1
(Ⅰ)证明:AB=AC
(Ⅱ)设二面角A-BD-C为60°,求B1C与平面BCD所成的角的大小
解析:本题考查线面垂直证明线面夹角的求法,第一问可取BC中点F,通过证明AF⊥平面BCC1,再证AF为BC的垂直平分线,第二问先作出线面夹角,即证四边形AFED是正方形可证平面DEF⊥平面BDC,从而找到线面夹角求解。此题两问也可建立空间直角坐标系利用向量法求解。
解法一:(Ⅰ)取BC中点F,连接EF,则EF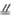
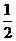
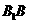 ,从而EF
,从而EF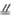 DA。
DA。
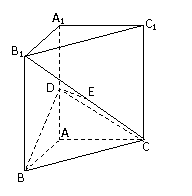

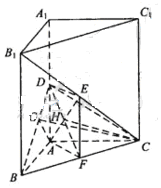
连接AF,则ADEF为平行四边形,从而AF//DE。又DE⊥平面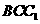 ,故AF⊥平面
,故AF⊥平面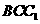 ,从而AF⊥BC,即AF为BC的垂直平分线,所以AB=AC。
,从而AF⊥BC,即AF为BC的垂直平分线,所以AB=AC。
(Ⅱ)作AG⊥BD,垂足为G,连接CG。由三垂线定理知CG⊥BD,故∠AGC为二面角A-BD-C的平面角。由题设知,∠AGC=600..
设AC=2,则AG=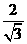 。又AB=2,BC=
。又AB=2,BC=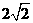 ,故AF=
,故AF=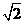 。
。
由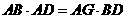 得2AD=
得2AD=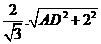 ,解得AD=
,解得AD=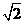 。
。
故AD=AF。又AD⊥AF,所以四边形ADEF为正方形。
因为BC⊥AF,BC⊥AD,AF∩AD=A,故BC⊥平面DEF,因此平面BCD⊥平面DEF。
连接AE、DF,设AE∩DF=H,则EH⊥DF,EH⊥平面BCD。
连接CH,则∠ECH为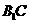 与平面BCD所成的角
与平面BCD所成的角
 因ADEF为正方形,AD=
因ADEF为正方形,AD=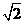 ,故EH=1,又EC=
,故EH=1,又EC=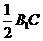 =2,
=2,
所以∠ECH=300,即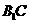 与平面BCD所成的角为300.
与平面BCD所成的角为300.
解法二:
(Ⅰ)以A为坐标原点,射线AB为x轴的正半轴,建立如图所示的直角坐标系A-xyz。
设B(1,0,0),C(0,b,0),D(0,0,c),则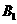 (1,0,2c),E(
(1,0,2c),E(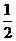 ,
,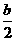 ,c).
,c).
于是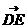 =(
=(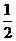 ,
,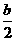 ,0),
,0),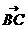 =(-1,b,0).由DE⊥平面
=(-1,b,0).由DE⊥平面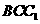 知DE⊥BC,
知DE⊥BC, 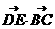 =0,求得b=1,所以 AB=AC。
=0,求得b=1,所以 AB=AC。
(Ⅱ)设平面BCD的法向量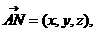 则
则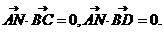
又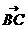 =(-1,1, 0),
=(-1,1, 0),
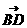 =(-1,0,c),故
=(-1,0,c),故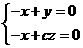
令x=1, 则y=1, z=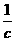 ,
,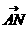 =(1,1,
=(1,1,
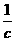 ).
).
又平面 的法向量
的法向量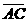 =(0,1,0)
=(0,1,0)
由二面角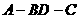 为60°知,
为60°知,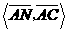 =60°,
=60°,
故 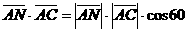 °,求得
°,求得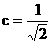
于是 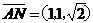 ,
, 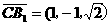
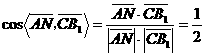 ,
,
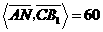 °
°
所以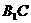 与平面
与平面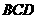 所成的角为30°
所成的角为30°
题型4:斜二测画法
例7.画正五棱柱的直观图,使底面边长为3cm侧棱长为5cm。
解析:先作底面正五边形的直观图,再沿平行于Z轴方向平移即可得
作法:
(1)画轴:画X′,Y′,Z′轴,使∠X′O′Y′=45°(或135°),∠X′O′Z′=90°。
(2)画底面:按X′轴,Y′轴画正五边形的直观图ABCDE。
(3)画侧棱:过A、B、C、D、E各点分别作Z′轴的平行线,并在这些平行线上分别截取AA′,BB′,CC′,DD′,EE。′
(4)成图:顺次连结A′,B′,C′,D′,F′,加以整理,去掉辅助线,改被遮挡的部分为虚线
点评:用此方法可以依次画出棱锥、棱柱、棱台等多面体的直观图。
例8.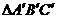 是正△ABC的斜二测画法的水平放置图形的直观图,若
是正△ABC的斜二测画法的水平放置图形的直观图,若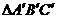 的面积为
的面积为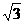 ,那么△ABC的面积为_______________。
,那么△ABC的面积为_______________。
解析: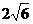 。
。
点评:该题属于斜二测画法的应用,解题的关键在于建立实物图元素与直观图元素之间的对应关系。特别底和高的对应关系。
题型5:平行投影与中心投影
例9.(1)如图,在正四面体A-BCD中,E、F、G分别是三角形ADC、ABD、BCD的中心,则△EFG在该正四面体各个面上的射影所有可能的序号是( )
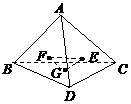
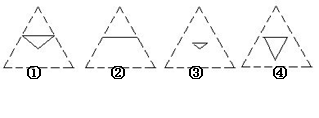
A.①③ B.②③④ C.③④ D.②④
(2)(2009宁夏海南卷理)(本小题满分12分)
如图,四棱锥S-ABCD 的底面是正方形,每条侧棱的长都是地面边长的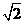 倍,P为侧棱SD上的点。
倍,P为侧棱SD上的点。
(Ⅰ)求证:AC⊥SD;
(Ⅱ)若SD⊥平面PAC,求二面角P-AC-D的大小
(Ⅲ)在(Ⅱ)的条件下,侧棱SC上是否存在一点E, 使得BE∥平面PAC。若存在,求SE:EC的值;若不存在,试说明理由。
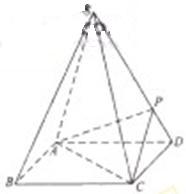
解法一:
(Ⅰ)连BD,设AC交BD于O,由题意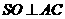 。在正方形ABCD中,
。在正方形ABCD中,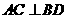 ,所以
,所以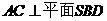 ,得
,得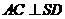 .
.
(Ⅱ)设正方形边长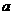 ,则
,则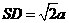 。
。
又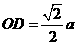 ,所以
,所以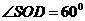 ,
,
连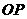 ,由(Ⅰ)知
,由(Ⅰ)知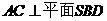 ,所以
,所以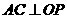
且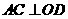 ,所以
,所以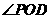 是二面角
是二面角 的平面角。
的平面角。
由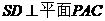 ,知
,知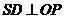 ,所以
,所以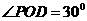 ,
,
即二面角 的大小为
的大小为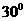 。
。
(Ⅲ)在棱SC上存在一点E,使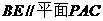
由(Ⅱ)可得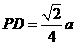 ,故可在
,故可在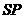 上取一点
上取一点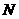 ,使
,使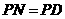 ,过
,过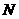 作
作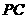 的平行线与
的平行线与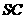 的交点即为
的交点即为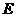 。连BN。在
。连BN。在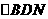 中知
中知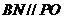 ,又由于
,又由于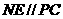 ,故平面
,故平面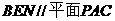 ,得
,得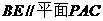 ,由于
,由于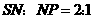 ,故
,故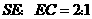 .
.
解法二:
(Ⅰ);连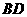 ,设
,设 交于
交于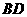 于
于 ,由题意知
,由题意知 .以O为坐标原点,
.以O为坐标原点,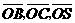 分别为
分别为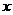 轴、
轴、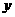 轴、
轴、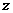 轴正方向,建立坐标系
轴正方向,建立坐标系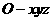 如图
如图
设底面边长为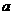 ,则高
,则高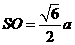 。
。
于是 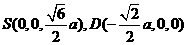
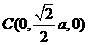
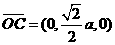
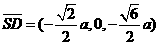
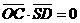
故 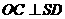
从而 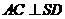
(Ⅱ)由题设知,平面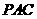 的一个法向量
的一个法向量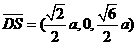 ,平面
,平面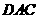 的一个法向量
的一个法向量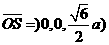 ,设所求二面角为
,设所求二面角为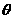 ,则
,则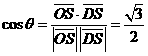 ,所求二面角的大小为
,所求二面角的大小为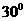
(Ⅲ)在棱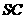 上存在一点
上存在一点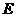 使
使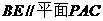 .
.
由(Ⅱ)知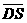 是平面
是平面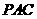 的一个法向量,
的一个法向量,
且 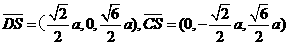
设 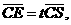
则 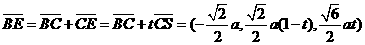
而 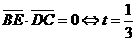
即当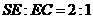 时,
时,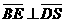
而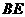 不在平面
不在平面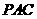 内,故
内,故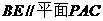
例10.多面体上,位于同一条棱两端的顶点称为相邻的,如图,正方体的一个顶点A在平面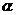 内,其余顶点在
内,其余顶点在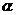 的同侧,正方体上与顶点A相邻的三个顶点到
的同侧,正方体上与顶点A相邻的三个顶点到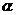 的距离分别为1,2和4,P是正方体的其余四个顶点中的一个,则P到平面
的距离分别为1,2和4,P是正方体的其余四个顶点中的一个,则P到平面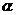 的距离可能是:
①3; ②4; ③5; ④6; ⑤7
的距离可能是:
①3; ②4; ③5; ④6; ⑤7
以上结论正确的为________________________(写出所有正确结论的编号)
 解析:如图,B、D、A1到平面
解析:如图,B、D、A1到平面 的距离分别为1、2、4,则D、A1的中点到平面
的距离分别为1、2、4,则D、A1的中点到平面 的距离为3,所以D1到平面
的距离为3,所以D1到平面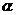 的距离为6;B、A1的中点到平面
的距离为6;B、A1的中点到平面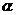 的距离为
的距离为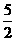 ,所以B1到平面
,所以B1到平面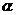 的距离为5;则D、B的中点到平面
的距离为5;则D、B的中点到平面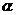 的距离为
的距离为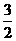 ,所以C到平面
,所以C到平面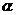 的距离为3;C、A1的中点到平面
的距离为3;C、A1的中点到平面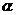 的距离为
的距离为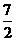 ,所以C1到平面
,所以C1到平面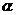 的距离为7;而P为C、C1、B1、D1中的一点,所以选①③④⑤。
的距离为7;而P为C、C1、B1、D1中的一点,所以选①③④⑤。
点评:该题将计算蕴涵于射影知识中,属于难得的综合题目
题型6:三视图
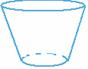
例11.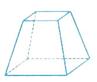 (1)画出下列几何体的三视图
(1)画出下列几何体的三视图
|
 解析:这二个几何体的三视图如下
解析:这二个几何体的三视图如下
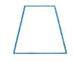


(2)如图,设所给的方向为物体的正前方,试画出它的三视图(单位:cm)
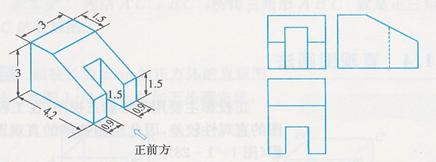
点评:画三视图之前,应把几何体的结构弄清楚,选择一个合适的主视方向。一般先画主视图,其次画俯视图,最后画左视图。画的时候把轮廓线要画出来,被遮住的轮廓线要画成虚线。物体上每一组成部分的三视图都应符合三条投射规律。
例12.某物体的三视图如下,试判断该几何体的形状
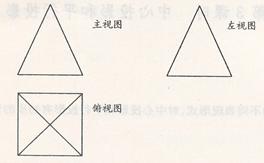
解析:该几何体为一个正四棱锥分析:三视图是从三个不同的方向看同一物体得到的三个视图。
点评:主视图反映物体的主要形状特征,主要体现物体的长和高,不反映物体的宽。而俯视图和主视图共同反映物体的长要相等。左视图和 俯视图共同反映物体的宽要相等。据此就不难得出该几何体的形状
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com