
题目列表(包括答案和解析)
例1.某地区有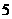 个工厂,由于电力紧缺,规定每个工厂在一周内必须选择某一天停电(选哪一天是等可能的),假定工厂之间的选择互不影响.
个工厂,由于电力紧缺,规定每个工厂在一周内必须选择某一天停电(选哪一天是等可能的),假定工厂之间的选择互不影响.
(1)求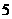 个工厂均选择星期日停电的概率;(2)求至少有两个工厂选择同一天停电的概率.
个工厂均选择星期日停电的概率;(2)求至少有两个工厂选择同一天停电的概率.
解:设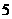 个工厂均选择星期日停电的事件为
个工厂均选择星期日停电的事件为 .
.
则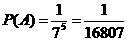 .
.
(2)设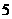 个工厂选择停电的时间各不相同的事件为
个工厂选择停电的时间各不相同的事件为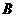 .
.
则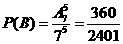 ,
,
至少有两个工厂选择同一天停电的事件为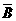 ,
,
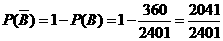 .
.
小结: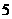 个工厂均选择星期日停电可看作
个工厂均选择星期日停电可看作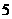 个相互独立事件.
个相互独立事件.
例2.某厂生产的 产品按每盒
产品按每盒 件进行包装,每盒产品均需检验合格后方可出厂.质检办法规定:从每盒
件进行包装,每盒产品均需检验合格后方可出厂.质检办法规定:从每盒 件
件 产品中任抽
产品中任抽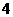 件进行检验,若次品数不超过
件进行检验,若次品数不超过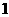 件,就认为该盒产品合格;否则,就认为该盒产品不合格.已知某盒
件,就认为该盒产品合格;否则,就认为该盒产品不合格.已知某盒 产品中有
产品中有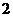 件次品.
件次品.
(1)求该盒产品被检验合格的概率;
(2)若对该盒产品分别进行两次检验,求两次检验得出的结果不一致的概率.
解: (1)从该盒 件产品中任抽
件产品中任抽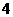 件,有等可能的结果数为
件,有等可能的结果数为 种,
种,
其中次品数不超过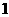 件有
件有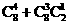 种,
种,
被检验认为是合格的概率为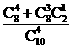
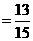 .
.
(2)两次检验是相互独立的,可视为独立重复试验,
因两次检验得出该盒产品合格的概率均为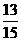 ,
,
故“两次检验得出的结果不一致”即两次检验中恰有一次是合格的概率为
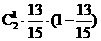
 .
.
答:该盒产品被检验认为是合格的概率为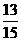 ;两次检验得出的结果不一致的概率为
;两次检验得出的结果不一致的概率为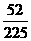 .
.
例3.假定在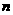 张票中有
张票中有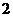 张奖票(
张奖票(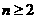 ),
),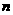 个人依次从中各抽一张,且后抽人不知道先抽人抽出的结果,(1)分别求第一,第二个抽票者抽到奖票的概率,(2)求第一,第二个抽票者都抽到奖票的概率.
个人依次从中各抽一张,且后抽人不知道先抽人抽出的结果,(1)分别求第一,第二个抽票者抽到奖票的概率,(2)求第一,第二个抽票者都抽到奖票的概率.
解:记事件 :第一个抽票者抽到奖票,记事件
:第一个抽票者抽到奖票,记事件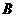 :第一个抽票者抽到奖票,
:第一个抽票者抽到奖票,
则(1)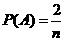 ,
,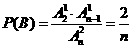 ,
,
(2)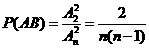
小结:因为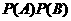 ≠
≠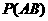 ,故A与B是不独立的.
,故A与B是不独立的.
例4. 将一枚骰子任意的抛掷 次,问
次,问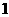 点出现(即
点出现(即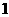 点的面向上)多少次的概率最大?
点的面向上)多少次的概率最大?
解:设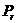 为
为 次抛掷中
次抛掷中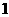 点出现
点出现 次的概率,则
次的概率,则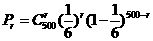 ,
,
∴ ,
,
∵由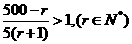 ,得
,得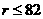 ,
,
即当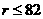 时,
时,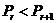 ,
,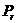 单调递增,当
单调递增,当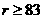 时,
时,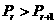 ,
,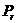 单调递减,
单调递减,
从而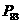 最大.
最大.
5.口袋里装有大小相同的黑、白两色的手套,黑色手套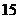 只,白色手套
只,白色手套 只,现从中随机地取出两只手套,如果两只是同色手套则甲获胜,两只手套颜色不同则乙获胜,则甲、乙获胜的机会是
( )
只,现从中随机地取出两只手套,如果两只是同色手套则甲获胜,两只手套颜色不同则乙获胜,则甲、乙获胜的机会是
( )
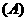 甲多
甲多
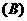 乙多
乙多  一样多
一样多 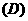 不确定
不确定
4.三个互相认识的人乘同一列火车,火车有 节车厢,则至少两人上了同一车厢的概率是
( )
节车厢,则至少两人上了同一车厢的概率是
( )
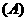
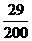
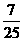

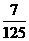
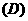
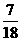
3. 件产品中有
件产品中有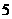 件次品,从中连续取两次,(1)取后不放回,(2)取后放回,则两次都取合格品的概率分别是
件次品,从中连续取两次,(1)取后不放回,(2)取后放回,则两次都取合格品的概率分别是 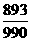 、
、 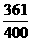 .
.
2.某射手射击一次,击中目标的概率是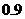 ,他连续射击
,他连续射击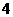 次,且各次射击是否击中目标相互之间没有影响,有下列结论:
次,且各次射击是否击中目标相互之间没有影响,有下列结论:
①他第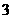 次击中目标的概率是
次击中目标的概率是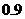 ;②他恰好击中目标
;②他恰好击中目标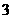 次的概率是
次的概率是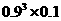 ;
;
③他至少击中目标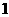 次的概率是
次的概率是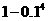 ,其中正确结论的序号 ①③ .
,其中正确结论的序号 ①③ .
1.下列各对事件
(1)运动员甲射击一次,“射中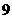 环”与“射中
环”与“射中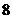 环”,
环”,
(2)甲、乙二运动员各射击一次, “甲射中 环”与“乙射中
环”与“乙射中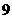 环”,
环”,
(3)甲、乙二运动员各射击一次, “甲、乙都射中目标”与,“甲、乙都没有射中目标”,
(4)甲、乙二运动员各射击一次, “至少有一人射中目标”与,“甲射中目标但乙没有射中目标”,是互斥事件的有 (1),(3) .相互独立事件的有 (2) .
3.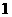 次试验中某事件发生的概率是
次试验中某事件发生的概率是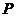 ,则
,则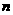 次独立重复试验中恰好发生
次独立重复试验中恰好发生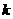 次的概率是 .
次的概率是 .
2.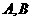 是相互独立事件,则
是相互独立事件,则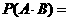 .
.
1.相互独立事件的概念: .
2.会计算事件在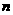 次独立重复试验中恰好发生
次独立重复试验中恰好发生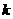 次的概率.
次的概率.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com