
题目列表(包括答案和解析)
例1.(1)若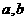 是正实数,且
是正实数,且 ,求
,求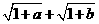 的最大值;
的最大值;
(2)若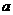 是正实数,且
是正实数,且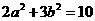 ,求
,求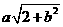 的最大值及相应的实数
的最大值及相应的实数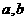 的值.
的值.
例2.商店经销某商品,年销售量为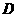 件,每件商品库存费用为
件,每件商品库存费用为 元,每批进货量为
元,每批进货量为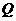 件,每次进货所需的费用为
件,每次进货所需的费用为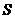 元,现假定商店在卖完该货物时立即进货,使库存存量平均为
元,现假定商店在卖完该货物时立即进货,使库存存量平均为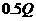 ,问每批进货量
,问每批进货量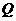 为多大时,整个费用最省?
为多大时,整个费用最省?
例3.已知 且
且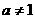 ,数列
,数列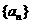 是首项为
是首项为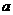 ,公比也为
,公比也为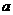 的等比数列,令
的等比数列,令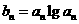
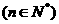 ,问是否存在实数
,问是否存在实数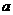 ,对任意正整数
,对任意正整数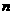 ,数列
,数列 中的每一项总小于它后面的项?证明你的结论.
中的每一项总小于它后面的项?证明你的结论.
6.若正数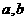 满足
满足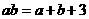 ,则
,则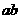 的取值范围是 .
的取值范围是 .
5.若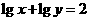 ,则
,则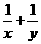 的最小值是
.
的最小值是
.
4.设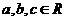 ,
, 且
且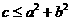 恒成立,则
恒成立,则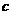 的最大值为
.
的最大值为
.
3.若实数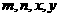 满足
满足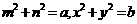
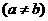 ,则
,则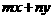 的最大值是( )
的最大值是( )
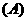
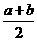
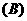
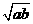

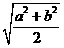
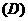
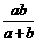
2.已知 ,且满足
,且满足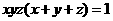 ,则
,则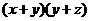 的最小值为( )
的最小值为( )
 2
2
 3
3  4
4  1
1
1.数列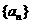 的通项公式是
的通项公式是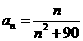 ,数列
,数列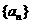 中最大的项是 ( )
中最大的项是 ( )
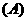 第9项
第9项 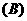 第10项
第10项  第8项和第9项
第8项和第9项  第9项和第10项
第9项和第10项
2.关于有关函数、不等式的实际应用问题:
这些问题大致分为两类:一是建立不等式解不等式;二是建立目标函数求最大、最小值.
1.利用均值不等式求最值:
常用公式: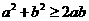 ,
,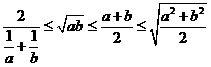 ,你知道这些公式的使用条件吗?等号成立的条件呢?使用
,你知道这些公式的使用条件吗?等号成立的条件呢?使用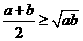 求最值时要满足“一正、二定、三相等”.
求最值时要满足“一正、二定、三相等”.
2.应用题中有一类是寻找最优化结果,通常是把问题转化为不等式模型,再求出极值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com