
题目列表(包括答案和解析)
2.正方体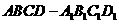 中,
中,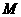 是
是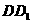 的中点,
的中点, 为底面正方形
为底面正方形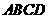 的中心,
的中心,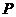 为棱
为棱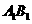 上任意一点,则直线
上任意一点,则直线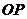 与直线
与直线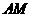 所成的角为 ( )
所成的角为 ( )
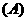
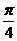
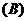
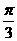

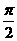
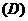 与
与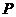 点的位置有关
点的位置有关
1.设正六棱锥的底面边长为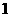 ,侧棱长为
,侧棱长为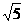 ,那么它的体积为( )
,那么它的体积为( )
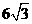
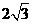

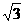
例1.正四棱锥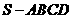 中,高
中,高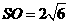 ,两相邻侧面所成角为
,两相邻侧面所成角为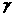 ,
,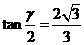 ,
,
(1)求侧棱与底面所成的角。(2)求侧棱 长、底面边长和斜高(见图)。
 解:(1) 作
解:(1) 作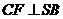 于
于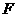 ,连结
,连结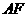 ,则
,则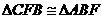 且
且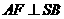 ,故
,故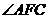 是相邻侧面所成二面角的平面角,连结
是相邻侧面所成二面角的平面角,连结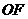 ,则
,则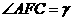 ,
, 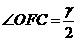 ,在
,在 与
与 中,
中, 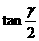 =
=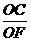 =
=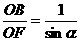 (其中
(其中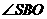 为
为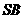 与底面所成的角,设为
与底面所成的角,设为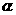 ) 故
) 故 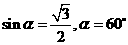 。
。
(2)在  中,侧棱
中,侧棱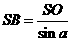 =
=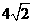 ,
,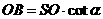
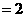
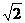 ,
,
∴边长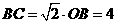 ;取
;取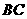 的中点
的中点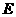 ,连结
,连结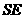 ,则
,则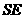 是正四棱锥的斜高,
是正四棱锥的斜高,
在 中,斜高
中,斜高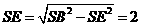
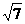 ;
;
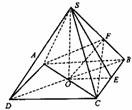
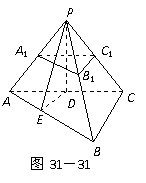
 例2.如图正三棱锥
例2.如图正三棱锥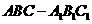 中,底面边长为
中,底面边长为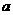 ,侧棱长为
,侧棱长为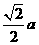 ,若经过对角线
,若经过对角线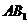 且与对角线
且与对角线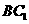 平行的平面交上底面于
平行的平面交上底面于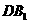 。(1)试确定
。(1)试确定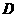 点的位置,并证明你的结论;(2)求平面
点的位置,并证明你的结论;(2)求平面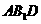 与侧面
与侧面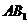 所成的角及平面
所成的角及平面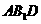 与底面所成的角;(3)求
与底面所成的角;(3)求 到平面
到平面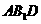 的距离。
的距离。
解:(1)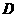 为
为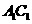 的中点。连结
的中点。连结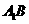 与
与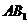 交于
交于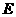 ,则
,则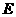 为
为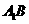 的中点,
的中点,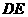 为平面
为平面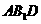 与平面
与平面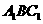 的交线,∵
的交线,∵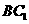 //平面
//平面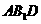
∴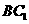 //
//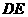 ,∴
,∴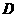 为
为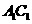 的中点。
的中点。
(2)过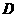 作
作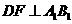 于
于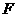 ,由正三棱锥的性质,
,由正三棱锥的性质,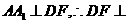 平面
平面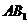 ,连结
,连结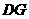 ,则
,则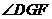 为平面
为平面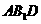 与侧面
与侧面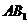 所成的角的平面角,可求得
所成的角的平面角,可求得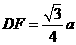 ,
,
由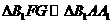 ,得
,得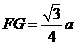 ,∴
,∴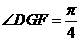
∵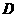 为
为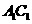 的中点,∴
的中点,∴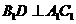 ,由正三棱锥的性质,
,由正三棱锥的性质,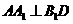 ,∴
,∴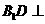 平面
平面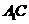
∴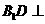
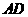 ,∴
,∴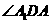 是平面
是平面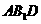 与上底面所成的角的平面角,可求得
与上底面所成的角的平面角,可求得
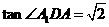 ,∴
,∴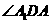

(3)过 作
作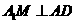 ,∵
,∵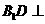 平面
平面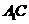 ,∴
,∴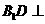
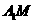 ,∴
,∴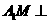 平面
平面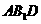
即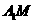 是
是 到平面
到平面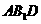 的距离,
的距离,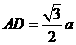 ,∴
,∴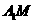
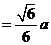
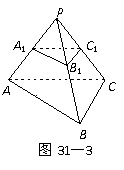
例3.如图,已知三棱锥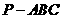 的侧面
的侧面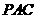 是底角为
是底角为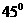 的等腰三角形,
的等腰三角形,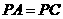 ,且该侧面垂直于底面,
,且该侧面垂直于底面,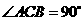 ,
,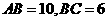 ,
,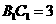 ,
,
(1)求证:二面角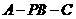 是直二面角;
是直二面角;
(2)求二面角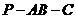 的正切值;
的正切值;
 (3)若该三棱锥被平行于底面的平面所截,得到一个几何体
(3)若该三棱锥被平行于底面的平面所截,得到一个几何体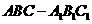 ,求几何体
,求几何体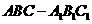 的侧面积.
的侧面积.
证 (1) 如图,在三棱锥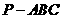 中,取
中,取 的中点
的中点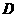 .
.
由题设知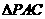 是等腰直角三角形,且
是等腰直角三角形,且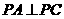 .
.
∴ 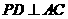 .
.
∵ 平面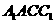
 平面
平面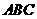 ,∴
,∴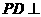 平面
平面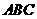 ,
,
∵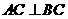 ∴
∴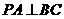 ,∴
,∴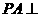 平面
平面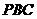 ,
,
∵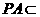 平面
平面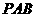 ,∴平面
,∴平面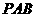
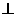 平面
平面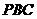 ,
,
 即二面角
即二面角 是直二面角.
是直二面角.
解 (2)作 ,
, 为垂足,则
为垂足,则 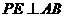 .∴
.∴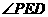 是二面角
是二面角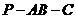 的平面角.在
的平面角.在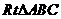 中,
中,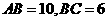 ,则
,则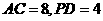
由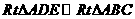 ,得
,得
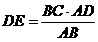 =
=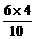 =
=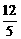 ,
,
∴ 所求正切为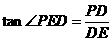 =
=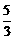 .
.
(3) ∵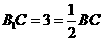 ∴
∴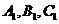 分别是
分别是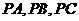 的中点.
的中点.
∴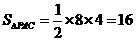 ,
, 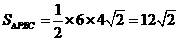 .
.
∵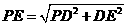 =
=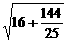 =
=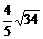 ,
,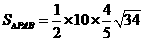
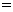
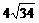 .
.
∴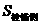
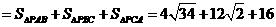 ,∴几何体
,∴几何体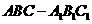 的侧面积
的侧面积 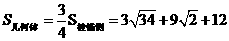
5.三棱柱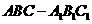 ,侧棱
,侧棱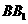 在下底面上的射影平行于
在下底面上的射影平行于 ,如果侧棱
,如果侧棱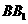 与底面所成的角为
与底面所成的角为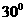 ,
,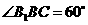 ,则
,则 的余弦为
的余弦为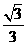
4.已知长方体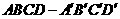 中,棱
中,棱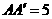 ,
,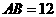 ,那么直线
,那么直线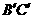 和平面
和平面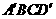 的距离是
的距离是 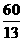 .
.
2.如果三棱锥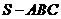 的底面是不等边三角形,侧面与底面所成的二面角都相等,且顶点
的底面是不等边三角形,侧面与底面所成的二面角都相等,且顶点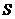 在底面的射影
在底面的射影 在
在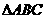 内,那么
内,那么 是
是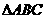 的(
的(  )
)
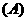 垂心
垂心
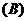 重心
重心  外心
外心 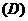 内心
内心
 .已知三棱锥
.已知三棱锥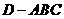 的三个侧面与底面全等,且
的三个侧面与底面全等,且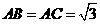 ,
,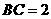 ,则以
,则以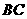 为棱,以面
为棱,以面 与面
与面 为面的二面角的大小是(
为面的二面角的大小是( 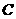 )
)
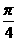
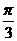

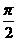
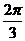
1.给出下列命题:
①底面是正多边形的棱锥是正棱锥;
②侧棱都相等的棱锥是正棱锥;
③侧棱和底面成等角的棱锥是正棱锥;
④侧面和底面所成二面角都相等的棱锥是正棱锥,
其中正确命题的个数是(  )
)


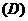
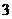
4.正棱锥的性质有
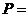 {四棱柱},
{四棱柱},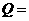 {平行六面体},
{平行六面体},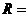 {长方体},
{长方体},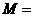 {正方体},
{正方体},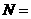 {正四棱柱},
{正四棱柱},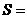 {直平行六面体},这六个集合之间的关系是
{直平行六面体},这六个集合之间的关系是
3. 叫正棱锥
2.正棱柱的性质有
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com