
题目列表(包括答案和解析)
5.若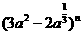 展开式中含有常数项,则正整数
展开式中含有常数项,则正整数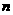 的最小值是 ( )
的最小值是 ( )
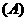

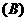
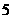

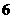
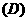

4.由等式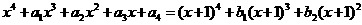
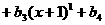 定义
定义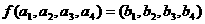 ,则
,则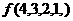 等于
( )
等于
( )
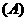
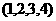
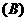



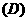
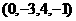
3.某电视台邀请了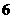 位同学的父母共
位同学的父母共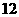 人,请这
人,请这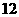 位家长中的
位家长中的 位介绍教育子女的情况,那么这
位介绍教育子女的情况,那么这 位中至多一对夫妻的选择方法为 ( )
位中至多一对夫妻的选择方法为 ( )
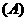
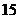 种
种 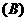
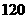 种
种 
 种
种 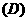
 种
种
2.某人制定了一项旅游计划,从 个旅游城市中选择
个旅游城市中选择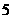 个进行游览.如果
个进行游览.如果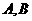 为必选
为必选
城市,并且在游览过程中必须按先 后
后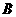 的次序经过
的次序经过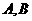 两城市(
两城市(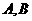 两城市可以不
两城市可以不
相邻),则有不同的游览线路 ( )
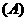
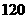 种
种 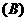
 种
种 
 种
种 
 种
种
1.甲、乙两人独立地解同一问题,甲解决这个问题的概率是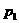 ,乙解决这个问题的概率是
,乙解决这个问题的概率是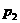 ,那么恰好有
,那么恰好有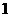 人解决这个问题的概率是 ( )
人解决这个问题的概率是 ( )
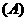
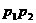
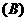
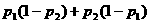

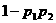
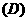

例1.对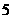 副不同的手套进行不放回抽取,甲先任取一只,乙再任取一只,然后甲又任取一只,最后乙再任取一只.
副不同的手套进行不放回抽取,甲先任取一只,乙再任取一只,然后甲又任取一只,最后乙再任取一只.
(Ⅰ)求下列事件的概率:①A:甲正好取得两只配对手套;②B:乙正好取得两只配对手套;
(Ⅱ)A与B是否独立?并证明你的结论.
(Ⅰ)①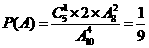 . ②
. ②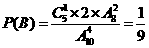 .
.
(Ⅱ)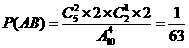 , 又
, 又 ,
,
∴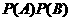 ≠
≠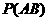 ,故
,故 与
与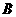 是不独立的.
是不独立的.
例2.甲、乙两人参加一次英语口语考试,已知在备选的 道试题中,甲能答对其中的
道试题中,甲能答对其中的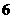 题,乙能答对其中的
题,乙能答对其中的 题,规定每次考试都从备选题中随机抽出
题,规定每次考试都从备选题中随机抽出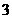 题进行测试,至少答对
题进行测试,至少答对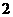 题才算合格.
题才算合格.
(Ⅰ)分别求甲答对试题数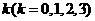 的概率;
的概率;
(Ⅱ)求甲、乙两人至少有一人考试合格的概率.
24.本小题主要考查概率统计的基础知识,运用数学知识解决问题的能力.满分12分.
解:(Ⅰ)依题意,甲答对试题数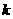 的概率分布如下:
的概率分布如下:
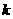

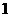
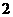
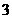
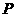
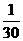
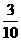
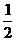
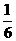
(Ⅱ)设甲、乙两人考试合格的事件分别为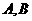 ,则
,则
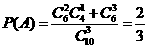 ,
,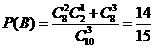 .
.
因为事件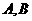 相互独立,
相互独立,
∴甲、乙两人考试均不合格的概率为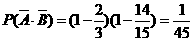
∴甲、乙两人至少有一人考试合格的概率为 ,
,
答:甲、乙两人至少有一人考试合格的概率为 .
.
例3.袋中装有 个红球和
个红球和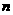 个白球,
个白球,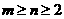 ,这些红球和白球除了颜色不同以外,其余都相同.从袋中同时取出
,这些红球和白球除了颜色不同以外,其余都相同.从袋中同时取出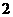 个球.
(1)若取出是
个球.
(1)若取出是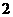 个红球的概率等于取出的是一红一白的
个红球的概率等于取出的是一红一白的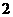 个球的概率的整数倍,试证
个球的概率的整数倍,试证 必为奇数;
必为奇数;
(2)在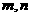 的数组中,若取出的球是同色的概率等于不同色的概率,试求失和
的数组中,若取出的球是同色的概率等于不同色的概率,试求失和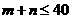 的所有数组
的所有数组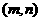 .
.
解:(1)设取出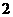 个球是红球的概率是取出的球是一红一白
个球是红球的概率是取出的球是一红一白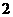 个球的概率的
个球的概率的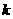 倍(
倍(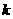 为整数)则有
为整数)则有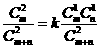
∴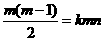 Þ
Þ 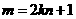 ∵
∵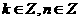 ,∴
,∴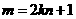 为奇数
为奇数
(2)由题意,有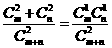 ,∴
,∴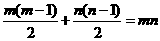 ∴
∴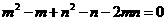 即
即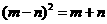 ,∵
,∵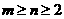 ,∴
,∴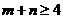 ,
∴
,
∴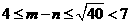 ,
,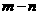 的取值只可能是
的取值只可能是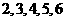 相应的
相应的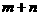 的取值分别是
的取值分别是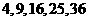 ,
,
∴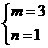 或
或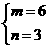 或
或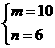 或
或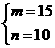 或
或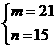 ,
注意到
,
注意到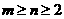 ∴
∴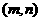 的数组值为
的数组值为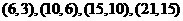
6.从黄瓜、白菜、油菜、扁豆 种蔬菜品种中选出
种蔬菜品种中选出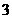 种,分别种在不同土质的三块土地上,其中黄瓜必须种植,不同的种植方法共
种,分别种在不同土质的三块土地上,其中黄瓜必须种植,不同的种植方法共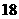 种.
种.
5.某班试用电子投票系统选举班干部候选人.全班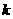 名同学都有选举权和被选举权,他们的编号分别为
名同学都有选举权和被选举权,他们的编号分别为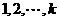 ,规定:同意按“
,规定:同意按“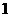 ”,不同意(含弃权)按“
”,不同意(含弃权)按“ ”,
”,
令
其中 ,且
,且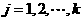 ,则同时同意第
,则同时同意第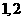 号同学当选的人数为(
号同学当选的人数为( 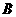 )
)
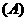
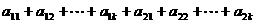
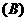
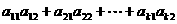

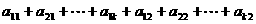
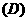
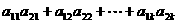
4.若
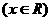 ,
,
则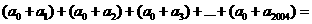
 (用数字作答) .
(用数字作答) .
3.某校高三年级举行一次演讲赛共有10位同学参赛,其中一班有3位,二班有2位,其它班有5位,若采用抽签的方式确定他们的演讲顺序,则一班有3位同学恰好被排在一起(指演讲序号相连),而二班的2位同学没有被排在一起的概率为 ( D )
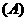
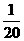

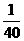
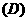

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com