
题目列表(包括答案和解析)
3.设y=8x2-lnx,则此函数在区间(0,1/4)和(1/2,1)内分别为( C )
A.单调递增,单调递减 B、单调递增,单调递增
C、单调递减,单调递增 D、单调递减,单调递减
2.关于函数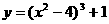 ,下列说法正确的是( B
)
,下列说法正确的是( B
)
(A)当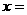 -2时,
-2时,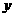 有极大值1 (B) 当
有极大值1 (B) 当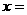 0时,
0时,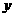 有极小值-63
有极小值-63
(C)当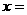 2时,
2时,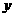 有极大值1 (D)
函数的最大值为1
有极大值1 (D)
函数的最大值为1
1.下列函数中,在x=0处的导数不等于零的是( A )
A.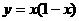 B.
B.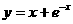
C.y=ln(1-x2) D.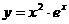
例1.设函数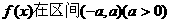 内为奇函数且可导,证明:
内为奇函数且可导,证明:
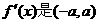 内的偶函数.
内的偶函数.
证明:对任意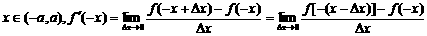
由于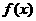 为奇函数,
为奇函数,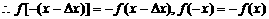 ,
,
于是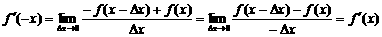 ,
,
因此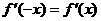 即
即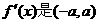 内的偶函数。
内的偶函数。
例2.已知函数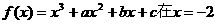 处取得极值,并且它
处取得极值,并且它
的图象与直线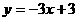 在点(1,0)处相切,求a、b、c的值.
在点(1,0)处相切,求a、b、c的值.
解:由曲线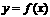 过(1,0)得
过(1,0)得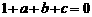 ① 又
① 又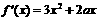 +b
+b
则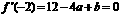 ②
②
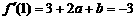 ③
③
解①②③得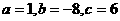 .
.
例3.已知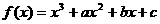 有极大值
有极大值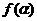 和极小值
和极小值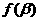 .
.
(1)求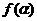 +
+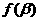 的值;
的值;
(2)设曲线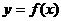 的极值点为A、B,求证:线段AB的中点在
的极值点为A、B,求证:线段AB的中点在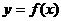 上.
上.
解:(1)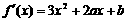 ,由于
,由于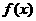 有极大值和极小值,
有极大值和极小值,
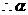 、
、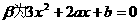 的两根,则
的两根,则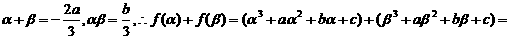
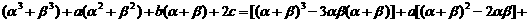
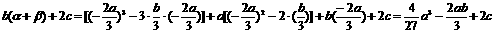
(2)设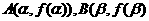 ,由
,由
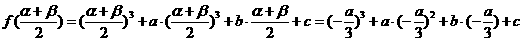
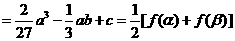 知AB的中点在
知AB的中点在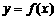 上。
上。
例4.设函数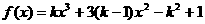 的驻点是0和4.
的驻点是0和4.
(1)求常数k的值;
(2)确定函数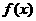 的单调区间;
的单调区间;
(3)求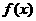 的极值。
的极值。
解:(1)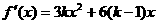 ,由于驻点是0和4,∴0和4是方程
,由于驻点是0和4,∴0和4是方程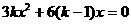 的两根,可求得
的两根,可求得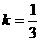
(2)由(1)可知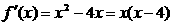 ,∴当
,∴当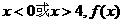 为增函数,
为增函数,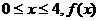 为减函数;
为减函数;
(3)由(2)可判断极大值为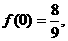 极小值为
极小值为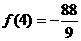
例5.求证: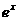

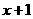 。
。
证明:(1)当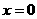 时,
时,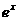 =1,
=1,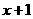 =1,命题成立;
=1,命题成立;
(2)当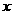 >0时,令
>0时,令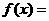
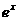
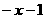 ,则
,则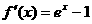 >0
>0
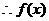 在(0,
在(0, )上为增函数
)上为增函数
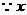 >0,
>0,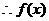 >
>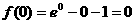 即
即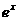
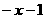 >0
>0

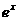 >
>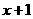 ;
;
(3)当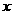 <0时,令
<0时,令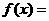
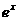
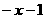 ,则
,则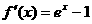 <0
<0
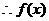 在(
在(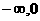 )上为减函数
)上为减函数
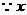 <0,
<0,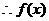 >
>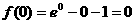 即
即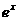
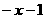 >0
>0

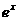 >
>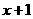
综合以上情况,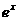

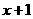 。
。
例6.已知函数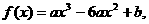 问是否存在实数a、b使f(x)在[-1,2]上取得最大值3,最小值-29,若存在,求出a、b的值.并指出函数的单调区间 . 若不存在,请说明理由 .
问是否存在实数a、b使f(x)在[-1,2]上取得最大值3,最小值-29,若存在,求出a、b的值.并指出函数的单调区间 . 若不存在,请说明理由 .
解: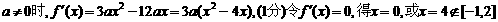 (舍)
(舍)
(1)a>0时,如下表
|
x |
(-1,0) |
0 |
(0,2) |
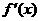 |
+ |
0 |
- |
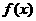 |
 |
最大值3 |
 |
∴当x=0时,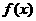 取得最大值, ∴b=3;
取得最大值, ∴b=3;
(2)a<0时,如下表
|
x |
(-1,0) |
0 |
(0,2) |
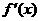 |
- |
0 |
+ |
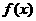 |
 |
最小值-29 |
 |
∴当x=0时,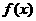 取得最小值, ∴b=-29(9分) 又f(2)=-16a-29,
f(-1)=-7a-29<f(2)
取得最小值, ∴b=-29(9分) 又f(2)=-16a-29,
f(-1)=-7a-29<f(2)
∴当x=2时, 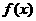 取得最大值,∴-16a-29=3, a=-2,
取得最大值,∴-16a-29=3, a=-2,
综上:a=2, b=3 或a=-2, b=-29。
例7.(2003年普通高等学校招生全国统一考试(天津卷、辽宁卷理19))
设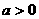 ,求函数
,求函数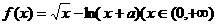 的单调区间.
的单调区间.
分析:本例主要考查导数的概念和计算,应用导数研究函数性质的方法及推理和运算能力。
解: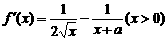 .
.
当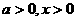 时
时 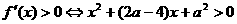 .
.
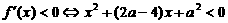
(i)当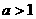 时,对所有
时,对所有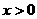 ,有
,有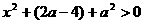 .
.
即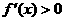 ,此时
,此时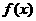 在
在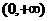 内单调递增.
内单调递增.
(ii)当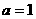 时,对
时,对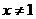 ,有
,有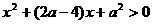 ,
,
即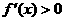 ,此时
,此时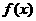 在(0,1)内单调递增,又知函数
在(0,1)内单调递增,又知函数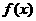 在x=1处连续,因此,函数
在x=1处连续,因此,函数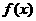 在(0,+
在(0,+ )内单调递增
)内单调递增
(iii)当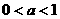 时,令
时,令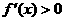 ,即
,即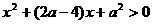 .
.
解得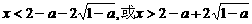 .
.
因此,函数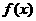 在区间
在区间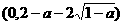 内单调递增,在区间
内单调递增,在区间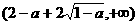 内也单调递增.
内也单调递增.
令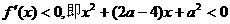 ,
,
解得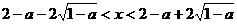 .
.
因此,函数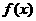 在区间
在区间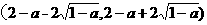 内单调递减.
内单调递减.
例8.⑴ 设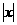 ≤1,求一个正常数a,使得x≤
≤1,求一个正常数a,使得x≤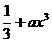 .
.
⑵ 设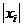 ≤1,
≤1,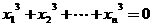 ,求证:
,求证: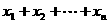 ≤
≤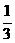 .
.
解:⑴
x≤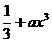 可化为
可化为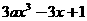 ≥0,令
≥0,令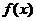 =
=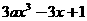 ,
,
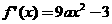 ,由
,由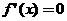 得,
得,
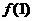 =3a-2≥0,
=3a-2≥0,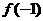 =-3a+4≥0,∴
=-3a+4≥0,∴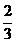 ≤
≤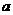 ≤
≤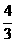 , ①
, ①
∴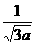 ∈[-1,1],
∈[-1,1],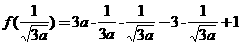 ≥0,即
≥0,即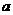 ≥
≥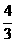 ②
②
由①、②得,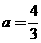 .
.
从而当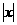 ≤1时,
≤1时,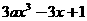 =
=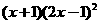 ≥0,即x≤
≥0,即x≤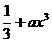 .
.
⑵ 由⑴知,对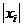 ≤1,有
≤1,有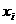 ≤
≤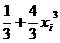 ,(i=1,2,…,n)
,(i=1,2,…,n)
将这n个式子求和,得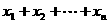 ≤
≤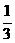 .
.
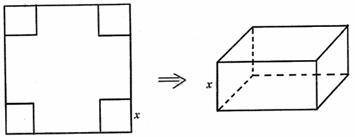
例9.从边长为2a的正方形铁片的四个角各截去一个边为x的正方形,再将四边向上折起,做成一个无盖的长方形铁盒,要求长方体的高度与底面边的比值不超过常数t(t>0)。试问当x取何值时,容量V有最大值。
解: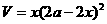 =
=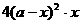
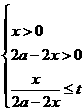

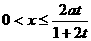
 函数V(
函数V(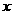 )=
)=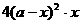 的定义域为
的定义域为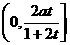
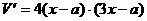 令
令 =0 得
=0 得 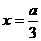
(1)当
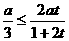 ,即
,即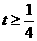 时,
时,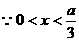 时,
时, >0 .V(
>0 .V(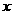 )为增函数;
)为增函数;
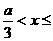
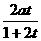 时,
时, <0 .V(
<0 .V(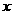 )为减函数;
)为减函数; V(
V(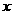 )在
)在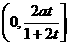 上有极大值V(
上有极大值V(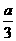 ),
),

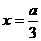 为唯一驻点,
为唯一驻点, 当
当
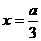 时,
时, 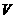 有最大值
有最大值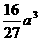 。
。
(2)当
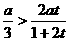 ,即
,即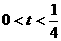 时,
时,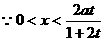 时,
时, >0恒成立;
>0恒成立;
 V(
V(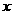 )为增函数;
)为增函数; 当
当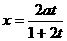 时,
时, 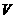 有最大值
有最大值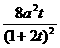 。
。
例10.某银行准备新设一种定期存款业务,经预测,存款量与利率的平方成正比,比例系数为K(K>0),贷款的利率为4.8%,又银行吸收的存款能全部放贷出去.(1)若存款的利率为x,x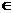 (0,0.048),试写出存款量g(x)及银行应支付给储户的利息h(x);(2)存款利率定为多少时,银行可获得最大收益?
(0,0.048),试写出存款量g(x)及银行应支付给储户的利息h(x);(2)存款利率定为多少时,银行可获得最大收益?
解:(1)由题意,存款量g(x)=Kx2,银行应支付的利息
h(x)=x·g(x)= Kx3
(2)设银行可获收益为y,则y=0.048·Kx2–Kx3
y /=K·0.096x–3 Kx2 令y /=0 即K×0.096x–3 Kx2=0
解得x=0 或x=0.032
又当x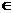 (0,0.032)时,y />0, x
(0,0.032)时,y />0, x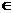 (0.032,0.048)时, y /<0
(0.032,0.048)时, y /<0
 y在(0,0.032)内单调递增,在(0.032,0.048) 单调递减
y在(0,0.032)内单调递增,在(0.032,0.048) 单调递减
故当x=0.032时,y在(0,0.048)内取得极大值,亦即最大值
答:存款利率为3.2%时,银行可获得最大收益
求闭区间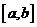 上的可导函数的最大(小)值的方法是:首先求出此函数在开区间
上的可导函数的最大(小)值的方法是:首先求出此函数在开区间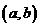 内的驻点,然后计算函数在驻点与端点处的值,并将它们进行比较,其中最大的一个即为最大值,最小的一个即为最小值,这里无须对各驻点讨论其是否为极大(小)值点。
内的驻点,然后计算函数在驻点与端点处的值,并将它们进行比较,其中最大的一个即为最大值,最小的一个即为最小值,这里无须对各驻点讨论其是否为极大(小)值点。
如果函数不在闭区间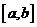 上可导,那么求函数的最大(小)值时,不仅要比较此函数在各驻点与端点处的值,还要比较函数在定义域内各不可导的点处的值。
上可导,那么求函数的最大(小)值时,不仅要比较此函数在各驻点与端点处的值,还要比较函数在定义域内各不可导的点处的值。
一般地,求在闭区间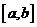 上连续,在开区间
上连续,在开区间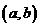 内可导的函数
内可导的函数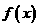 在闭区间
在闭区间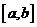 上最值的步骤为:
上最值的步骤为:
⑴求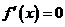 在区间
在区间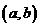 内的根,即导数为0的点(不必确定它是极大值点还是极小值点),求出这些导数为0的点的函数值;
内的根,即导数为0的点(不必确定它是极大值点还是极小值点),求出这些导数为0的点的函数值;
⑵求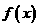 在闭区间
在闭区间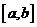 两端点处的函数值,即
两端点处的函数值,即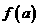 与
与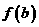 ;
;
⑶将导数为0的函数值与两端点处的函数值进行比较,其中最大的一个即为最大值,最小的一个即为最小值。
若函数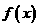 在某个区间内可导,则当
在某个区间内可导,则当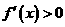 时,
时,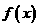 在此区间上为单调增函数;而当
在此区间上为单调增函数;而当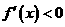 时,
时,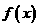 在此区间上为单调减函数。利用上述性质,可以研究函数的单调性。
在此区间上为单调减函数。利用上述性质,可以研究函数的单调性。
注意点:
(1)同一函数的两个单调区间不能并起来
(2)求函数的单调区间,求导的方法不是唯一的方法,也不一定是最好的方法,但它是一种一般性的方法。
10.已知函数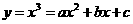 的图像过点
的图像过点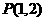 .过
.过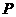 点的切线与图象仅
点的切线与图象仅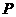 点一个公共点,又知切线斜率的最小值为2,求
点一个公共点,又知切线斜率的最小值为2,求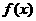 的解析式
的解析式
|

|
版权所有:()
版权所有:()
9..曲线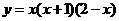 上有一点
上有一点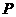 ,它的坐标均为整数,且过
,它的坐标均为整数,且过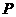 点的切线斜率为正数,求此点坐标及相应的切线方程.
点的切线斜率为正数,求此点坐标及相应的切线方程.
8.已知函数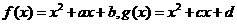 . 若
. 若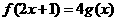 ,且
,且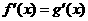 ,
,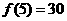 ,求
,求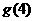 .
.
7.设曲线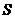 :
: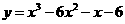 ,
,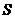 在哪一点处的切线斜率最小?设此点为
在哪一点处的切线斜率最小?设此点为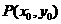
求证:曲线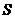 关于
关于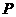 点中心对称.
点中心对称.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com