
题目列表(包括答案和解析)
3.(2010重庆文)(8)若直线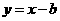 与曲线
与曲线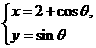 (
(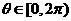 )有两个不同的公共点,则实数
)有两个不同的公共点,则实数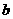 的取值范围为
的取值范围为
(A)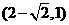 (B)
(B)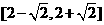
(C) (D)
(D)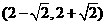
[答案]D
解析: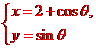 化为普通方程
化为普通方程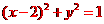 ,表示圆,
,表示圆,
 因为直线与圆有两个不同的交点,所以
因为直线与圆有两个不同的交点,所以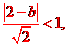 解得
解得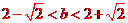
法2:利用数形结合进行分析得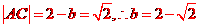
同理分析,可知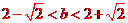
2.(2010安徽文)(4)过点(1,0)且与直线x-2y-2=0平行的直线方程是
(A)x-2y-1=0 (B)x-2y+1=0 (C)2x+y-2=0 (D)x+2y-1=0
[答案]A
[解析]设直线方程为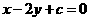 ,又经过
,又经过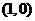 ,故
,故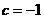 ,所求方程为
,所求方程为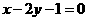 .
.
[方法技巧]因为所求直线与与直线x-2y-2=0平行,所以设平行直线系方程为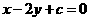 ,代入此直线所过的点的坐标,得参数值,进而得直线方程.也可以用验证法,判断四个选项中方程哪一个过点(1,0)且与直线x-2y-2=0平行.
,代入此直线所过的点的坐标,得参数值,进而得直线方程.也可以用验证法,判断四个选项中方程哪一个过点(1,0)且与直线x-2y-2=0平行.
1.(2010江西理)8.直线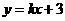 与圆
与圆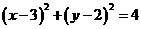 相交于M,N两点,若
相交于M,N两点,若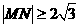 ,则k的取值范围是
,则k的取值范围是
A. 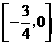 B.
B.
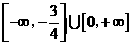 C.
C. 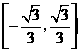 D.
D.
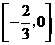
[答案]A
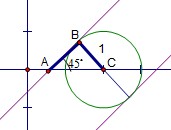
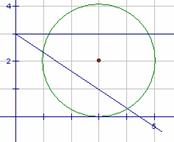 [解析]考查直线与圆的位置关系、点到直线距离公式,重点考察数形结合的运用.
[解析]考查直线与圆的位置关系、点到直线距离公式,重点考察数形结合的运用.
解法1:圆心的坐标为(3.,2),且圆与y轴相切.当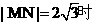 ,由点到直线距离公式,解得
,由点到直线距离公式,解得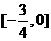 ;
;
解法2:数形结合,如图由垂径定理得夹在两直线之间即可,
不取 ,排除B,考虑区间不对称,排除C,利用斜率估值,选A
,排除B,考虑区间不对称,排除C,利用斜率估值,选A
2010年高考题
2.(2010全国卷2理)(18)(本小题满分12分)
已知数列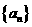 的前
的前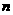 项和
项和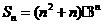 .
.
(Ⅰ)求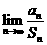 ;
;
(Ⅱ)证明: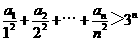 .
.
[命题意图]本试题主要考查数列基本公式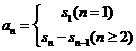 的运用,数列极限和数列不等式的证明,考查考生运用所学知识解决问题的能力.
的运用,数列极限和数列不等式的证明,考查考生运用所学知识解决问题的能力.
1.(2010湖南文)20.(本小题满分13分)
给出下面的数表序列:

其中表n(n=1,2,3  )有n行,第1行的n个数是1,3,5,
)有n行,第1行的n个数是1,3,5, 2n-1,从第2行起,每行中的每个数都等于它肩上的两数之和。
2n-1,从第2行起,每行中的每个数都等于它肩上的两数之和。
(I)写出表4,验证表4各行中数的平均数按从上到下的顺序构成等比数列,并将结论推广到表n(n≥3)(不要求证明);
(II)每个数列中最后一行都只有一个数,它们构成数列1,4,12 ,记此数列为
,记此数列为
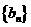 求和:
求和: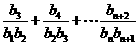
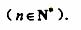



6.(2010湖南理)15.若数列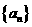 满足:对任意的
满足:对任意的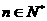 ,只有有限个正整数
,只有有限个正整数 使得
使得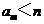 成立,记这样的
成立,记这样的 的个数为
的个数为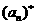 ,则得到一个新数列
,则得到一个新数列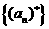 .例如,若数列
.例如,若数列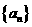 是
是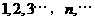 ,则数列
,则数列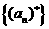 是
是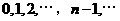 .已知对任意的
.已知对任意的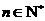 ,
,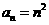 ,则
,则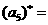 ,
,
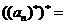 .
.
5.(2010天津文)(15)设{an}是等比数列,公比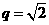 ,Sn为{an}的前n项和。记
,Sn为{an}的前n项和。记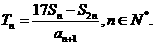 设
设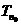 为数列{
为数列{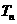 }的最大项,则
}的最大项,则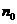 =
。
=
。
[答案]4
[解析]本题主要考查了等比数列的前n项和公式与通项及平均值不等式的应用,属于中等题。

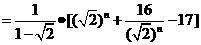 因为
因为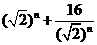 ≧8,当且仅当
≧8,当且仅当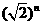 =4,即n=4时取等号,所以当n0=4时Tn有最大值。
=4,即n=4时取等号,所以当n0=4时Tn有最大值。
[温馨提示]本题的实质是求Tn取得最大值时的n值,求解时为便于运算可以对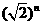 进行换元,分子、分母都有变量的情况下通常可以采用分离变量的方法求解.
进行换元,分子、分母都有变量的情况下通常可以采用分离变量的方法求解.
4.(2010浙江文)(14)在如下数表中,已知每行、每列中的树都成等差数列,
那么,位于下表中的第n行第n+1列的数是 。

答案: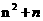
3.(2010辽宁理)(16)已知数列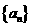 满足
满足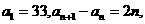 则
则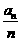 的最小值为__________.
的最小值为__________.
[答案]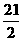
[命题立意]本题考查了递推数列的通项公式的求解以及构造函数利用导数判断函数单调性,考查了同学们综合运用知识解决问题的能力。
[解析]an=(an-an-1)+(an-1-an-2)+…+(a2-a1)+a1=2[1+2+…(n-1)]+33=33+n2-n
所以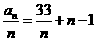
设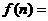
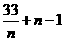 ,令
,令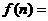
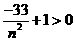 ,则
,则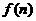 在
在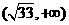 上是单调递增,在
上是单调递增,在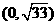 上是递减的,因为n∈N+,所以当n=5或6时
上是递减的,因为n∈N+,所以当n=5或6时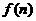 有最小值。
有最小值。
又因为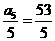 ,
,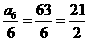 ,所以,
,所以,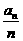 的最小值为
的最小值为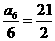
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com