
题目列表(包括答案和解析)
1.(2008广东)将正三棱柱截去三个角(如图1所示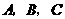 分别是
分别是 三边的中点)得到几何体如图2,则该几何体按图2所示方向的侧视图(或称左视图)为( )
三边的中点)得到几何体如图2,则该几何体按图2所示方向的侧视图(或称左视图)为( )
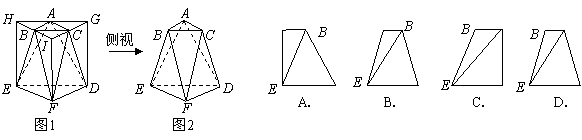

答案 A
20.(本小题满分13分)
某高速公路收费站入口处的安全标识墩如图4所示。墩的上半部分是正四棱锥
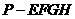 ,下半部分是长方体
,下半部分是长方体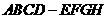 。图5、图6分别是该标识墩的正(主)视图和俯视图。
。图5、图6分别是该标识墩的正(主)视图和俯视图。
(1)请画出该安全标识墩的侧(左)视图;
(2)求该安全标识墩的体积;
(3)证明:直线 平面
平面 .
.
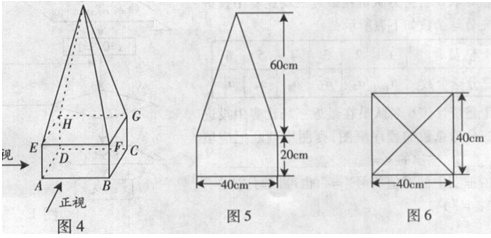
[解析](1)侧视图同正视图,如下图所示.
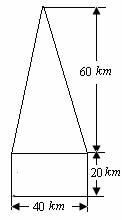
(2)该安全标识墩的体积为:
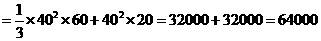

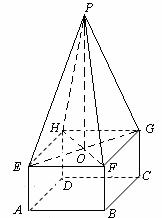
(3)如图,连结EG,HF及 BD,EG与HF相交于O,连结PO.
由正四棱锥的性质可知, 平面EFGH ,
平面EFGH , 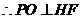
又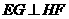
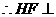 平面PEG
平面PEG
又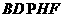
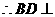 平面PEG;
平面PEG;
2008年高考题
19.若球O1、O2表示面积之比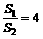 ,则它们的半径之比
,则它们的半径之比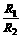 =_____________.
=_____________.
答案 2
三、解答题
18.已知三个球的半径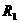 ,
,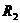 ,
,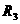 满足
满足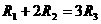 ,则它们的表面积
,则它们的表面积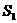 ,
,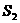 ,
,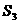 ,
,
满足的等量关系是___________.
答案 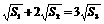
17.如图球O的半径为2,圆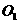 是一小圆,
是一小圆,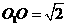 ,A、B
,A、B
是圆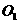 上两点,若A,B两点间的球面距离为
上两点,若A,B两点间的球面距离为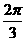 ,则
,则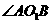 =
.
=
.
答案 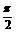
16.体积为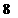 的一个正方体,其全面积与球
的一个正方体,其全面积与球 的表面积相等,则球
的表面积相等,则球 的体积等于
.
的体积等于
.
答案 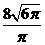
15.正三棱柱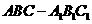 内接于半径为
内接于半径为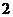 的球,若
的球,若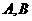 两点的球面距离为
两点的球面距离为 ,则正三棱
,则正三棱
柱的体积为 .
答案 8
14. 直三棱柱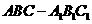 的各顶点都在同一球面上,若
的各顶点都在同一球面上,若
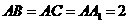 ,
,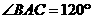 ,则此球的表面积等于
。
,则此球的表面积等于
。
解:在 中
中 ,
,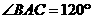 ,可得
,可得 ,由正弦定理,可得
,由正弦定理,可得 [来源:高&考%资(源#网]
[来源:高&考%资(源#网]
外接圆半径r=2,设此圆圆心为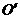 ,球心为
,球心为 ,在
,在 中,易得球半径
中,易得球半径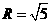 ,故此球的表面积为
,故此球的表面积为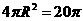 .
.
13.设某几何体的三视图如下(尺寸的长度单位为m)。
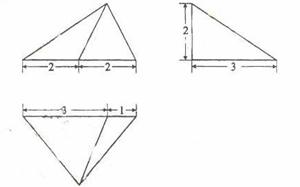
则该几何体的体积为
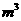
答案答案 4
12.若某几何体的三视图(单位: )如图所示,则此几何体的体积是
)如图所示,则此几何体的体积是
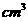 .
.
答案 18
[解析]该几何体是由二个长方体组成,下面体积为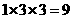 ,上面的长方体体积为
,上面的长方体体积为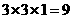 ,因此其几何体的体积为18
,因此其几何体的体积为18
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com