
题目列表(包括答案和解析)
12.(2009安徽卷文)(本小题满分12分) 在 ABC中,C-A=
ABC中,C-A= , sinB=
, sinB= 。
。
(I)求sinA的值;(II)设AC= ,求
,求 ABC的面积。
ABC的面积。
[思路](1)依据三角函数恒等变形可得关于 的式子,这之中要运用到倍角公式;
的式子,这之中要运用到倍角公式;
(2)应用正弦定理可得出边长,进而用面积公式可求出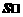 .
.
解(1)∵ ∴
∴
∴
∴
又 ∴
∴
(2)如图,由正弦定理得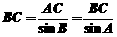 ∴
∴

∴ .
.
11.(2009安徽卷理)在 ABC中,
ABC中, , sinB=
, sinB=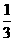 .
.
(I)求sinA的值;
(II)设AC= ,求
,求 ABC的面积.
ABC的面积.
解:(Ⅰ)由 ,且
,且 ,∴
,∴ ,∴
,∴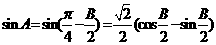 ,
,
 ∴
∴ ,又
,又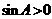 ,∴
,∴
(Ⅱ)如图,由正弦定理得
∴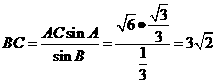 ,又
,又

∴
10.(2009全国卷Ⅱ文)(本小题满分12分)设△ABC的内角A、B、C的对边长分别为a、b、c,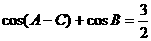 ,
, ,求B.
,求B.
解析:本题考查三角函数化简及解三角形的能力,关键是注意角的范围对角的三角函数值的制约,并利用正弦定理得到sinB= (负值舍掉),从而求出B=
(负值舍掉),从而求出B= 。
。
解:由 cos(A C)+cosB=
C)+cosB= 及B=π
及B=π (A+C)得 cos(A
(A+C)得 cos(A C)
C) cos(A+C)=
cos(A+C)=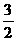 ,
,
cosAcosC+sinAsinC (cosAcosC
(cosAcosC sinAsinC)=
sinAsinC)=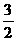 ,
,
sinAsinC= .
.
又由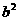 =ac及正弦定理得
=ac及正弦定理得

故  ,
,
 或
或  (舍去),
(舍去),
于是 B= 或 B=
或 B= .
.
又由 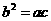 知
知 或
或
所以 B= 。
。
10.(2009山东卷文)(本小题满分12分)设函数f(x)=2 在
在 处取最小值.
处取最小值.
(1)求 .的值;
.的值;
(2)在 ABC中,
ABC中,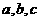 分别是角A,B,C的对边,已知
分别是角A,B,C的对边,已知
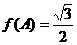 ,
,
求角C.
解 (1)



因为函数f(x)在 处取最小值,所以
处取最小值,所以 ,由诱导公式知
,由诱导公式知 ,因为
,因为 ,所以
,所以 .所以
.所以
(2)因为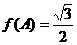 ,所以
,所以 ,因为角A为
,因为角A为 ABC的内角,所以
ABC的内角,所以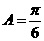 .又因为
.又因为 所以由正弦定理,得
所以由正弦定理,得 ,也就是
,也就是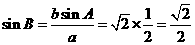 ,
,
因为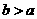 ,所以
,所以 或
或 .
.
当 时,
时, ;当
;当 时,
时, .
.
[命题立意]:本题主要考查了三角函数中两角和差的弦函数公式、二倍角公式和三角函数的性质,并利用正弦定理解得三角形中的边角.注意本题中的两种情况都符合.
9.(2009山东卷理)(本小题满分12分)设函数f(x)=cos(2x+ )+sin
)+sin x.
x.
(1) 求函数f(x)的最大值和最小正周期.
(2) 设A,B,C为 ABC的三个内角,若cosB=
ABC的三个内角,若cosB= ,
, ,且C为锐角,求sinA.
,且C为锐角,求sinA.
解 (1)f(x)=cos(2x+ )+sin
)+sin x.=
x.=
所以函数f(x)的最大值为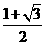 ,最小正周期
,最小正周期 .
.
(2) =
=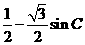 =-
=-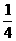 , 所以
, 所以 , 因为C为锐角, 所以
, 因为C为锐角, 所以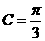 ,
,
又因为在 ABC 中,
cosB=
ABC 中,
cosB= , 所以
, 所以 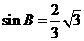 , 所以
, 所以
 .
.
8.(2009北京理) 在 中,角
中,角 的对边分别为
的对边分别为 ,
, 。
。
(Ⅰ)求 的值;
的值;
(Ⅱ)求 的面积.
的面积.
[解析] 本题主要考查三角形中的三角函数变换及求值、诱导公式、三角形的面积公式等基础知识,主要考查基本运算能力.
解(Ⅰ)∵A、B、C为△ABC的内角,且 ,
,
∴ ,
,
∴ .
.
(Ⅱ)由(Ⅰ)知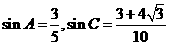 ,
,
又∵ ,∴在△ABC中,由正弦定理,得
,∴在△ABC中,由正弦定理,得
∴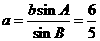 .
.
∴△ABC的面积 .
.
7.(2009浙江文)(本题满分14分)在 中,角
中,角 所对的边分别为
所对的边分别为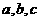 ,且满足
,且满足 ,
, .
.
(I)求 的面积; (II)若
的面积; (II)若 ,求
,求 的值.
的值.
解(Ⅰ)
又 ,
, ,而
,而 ,所以
,所以 ,所以
,所以 的面积为:
的面积为: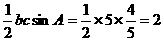
(Ⅱ)由(Ⅰ)知 ,而
,而 ,所以
,所以
所以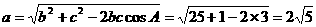
6.(2009浙江理)(本题满分14分)在 中,角
中,角 所对的边分别为
所对的边分别为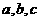 ,且满足
,且满足 ,
, .
.
(I)求 的面积; (II)若
的面积; (II)若 ,求
,求 的值.
的值.
解 (1)因为 ,
, ,又由
,又由
得
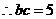 ,
,
(2)对于 ,又
,又 ,
, 或
或 ,由余弦定理得
,由余弦定理得
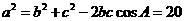 ,
,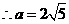
5.(2009全国卷Ⅰ理)在 中,内角A、B、C的对边长分别为
中,内角A、B、C的对边长分别为 、
、 、
、 ,已知
,已知 ,且
,且 求b
求b
分析:此题事实上比较简单,但考生反应不知从何入手.对已知条件(1) 左侧是二次的右侧是一次的,学生总感觉用余弦定理不好处理,而对已知条件(2)
左侧是二次的右侧是一次的,学生总感觉用余弦定理不好处理,而对已知条件(2)  过多的关注两角和与差的正弦公式,甚至有的学生还想用现在已经不再考的积化和差,导致找不到突破口而失分.
过多的关注两角和与差的正弦公式,甚至有的学生还想用现在已经不再考的积化和差,导致找不到突破口而失分.
解法一:在 中
中 则由正弦定理及余弦定理有:
则由正弦定理及余弦定理有: 化简并整理得:
化简并整理得: .又由已知
.又由已知
 .解得
.解得 .
.
解法二:由余弦定理得:
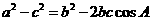 .又
.又 ,
,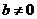 .
.
所以 ①
①
又 ,
,
 ,即
,即
由正弦定理得 ,故
,故 ②
②
由①,②解得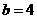 .
.
评析:从08年高考考纲中就明确提出要加强对正余弦定理的考查.在备考中应注意总结、提高自己对问题的分析和解决能力及对知识的灵活运用能力.另外提醒:两纲中明确不再考的知识和方法了解就行,不必强化训练。
4.(2009湖南卷文)在锐角 中,
中, 则
则 的值等于
,
的值等于
,
 的取值范围为 .
的取值范围为 .
答案 2
解析 设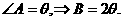 由正弦定理得
由正弦定理得

由锐角 得
得 ,
,
又 ,故
,故 ,
,
 [来源:高&考%资(源#网]
[来源:高&考%资(源#网]
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com