
题目列表(包括答案和解析)
3.(2010辽宁理)(17)(本小题满分12分)
在△ABC中,a, b, c分别为内角A, B, C的对边,且

(Ⅰ)求A的大小;
(Ⅱ)求 的最大值.
的最大值.
解:
(Ⅰ)由已知,根据正弦定理得
即 
由余弦定理得 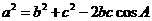
故  ,A=120°
……6分
,A=120°
……6分
(Ⅱ)由(Ⅰ)得:


故当B=30°时,sinB+sinC取得最大值1。 ……12分
2.(2010辽宁文)(17)(本小题满分12分)
在 中,
中,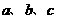 分别为内角
分别为内角 的对边,
的对边,
且
(Ⅰ)求 的大小;
的大小;
(Ⅱ)若 ,试判断
,试判断 的形状.
的形状.
解:(Ⅰ)由已知,根据正弦定理得
即
由余弦定理得
故
(Ⅱ)由(Ⅰ)得
又 ,得
,得
因为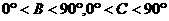 ,
,
故
所以 是等腰的钝角三角形。
是等腰的钝角三角形。
1. (2010陕西文)17.(本小题满分12分)
(2010陕西文)17.(本小题满分12分)
在△ABC中,已知B=45°,D是BC边上的一点,
AD=10,AC=14,DC=6,求AB的长.
解 在△ADC中,AD=10,AC=14,DC=6,
由余弦定理得
cos
 =
= ,
,

 ADC=120°,
ADC=120°,  ADB=60°
ADB=60°
在△ABD中,AD=10,  B=45°,
B=45°,  ADB=60°,
ADB=60°,
由正弦定理得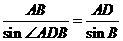 ,
,
 AB=
AB= .
.
6.(2010江苏卷)13、在锐角三角形ABC,A、B、C的对边分别为a、b、c, ,则
,则 =_________。
=_________。
[解析] 考查三角形中的正、余弦定理三角函数知识的应用,等价转化思想。一题多解。
(方法一)考虑已知条件和所求结论对于角A、B和边a、b具有轮换性。
当A=B或a=b时满足题意,此时有: ,
, ,
,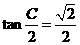 ,
,
 ,
, =
4。
=
4。
(方法二) ,
,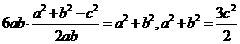
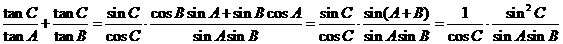
5.(2010广东理)11.已知a,b,c分别是△ABC的三个内角A,B,C所对的边,若a=1,b=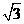 , A+C=2B,则sinC= .
, A+C=2B,则sinC= .
答案1.
解析:由A+C=2B及A+ B+ C=180°知,B =60°.由正弦定理知, ,即
,即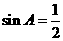 .由
.由 知,
知, ,则
,则 ,
,
 ,
,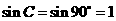
4.(2010北京理)(10)在△ABC中,若b = 1,c =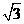 ,
, ,则a =
。
,则a =
。
答案 1
3.(2010北京文)(10)在 中。若
中。若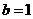 ,
, ,
, ,则a= 。
,则a= 。
答案:1
2.(2010山东文)(15) 在 中,角A,B,C所对的边分别为a,b,c,若
中,角A,B,C所对的边分别为a,b,c,若 ,
, ,
, ,则角A的大小为
.
,则角A的大小为
.
答案:
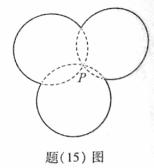
1.(2010重庆文)(15)如题(15)图,图中的实线是由三段圆弧连接而成的一条封闭曲线 ,各段弧所在的圆经过同一点
,各段弧所在的圆经过同一点 (点
(点 不在
不在 上)且半径相等. 设第
上)且半径相等. 设第 段弧所对的圆心角为
段弧所对的圆心角为 ,
, 则
则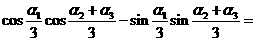 ____________ .
____________ .
解析: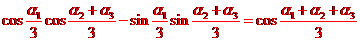
又 ,所以
,所以
7.(2010湖北理)3.在 中,a=15,b=10,A=60°,则
中,a=15,b=10,A=60°,则 =
=
A -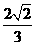 B
B 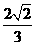 C -
C - D
D 
[答案]D
[解析]根据正弦定理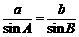 可得
可得 解得
解得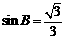 ,又因为
,又因为 ,则
,则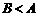 ,故B为锐角,所以
,故B为锐角,所以 ,故D正确.
,故D正确.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com