
题目列表(包括答案和解析)
2.(2009厦门一中)把函数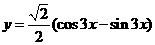 的图象适当变化就可以得到
的图象适当变化就可以得到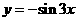 的图象,这个变化可以是 ( )
的图象,这个变化可以是 ( )
A.沿x轴方向向右平移 B.沿x轴方向向左平移
B.沿x轴方向向左平移
C.沿x轴方向向右平移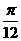 D.沿x轴方向向左平移
D.沿x轴方向向左平移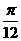
答案 D
1.(2009福建省)为了得到函数y= 的图象,可以将函数y=sin2x的图象( )
的图象,可以将函数y=sin2x的图象( )
A.向左平移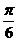 个单位长度,再向下平移
个单位长度,再向下平移 个单位长度
个单位长度
B.向右平移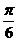 个单位长度,再向上平移
个单位长度,再向上平移 个单位长度
个单位长度
C.向左平移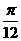 个单位长度,再向下平移
个单位长度,再向下平移 个单位长度
个单位长度
D.向右平移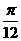 个单位长度,再向上平移
个单位长度,再向上平移 个单位长度
个单位长度
答案 D
10.(2009深圳一模)已知函数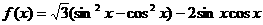 .
.
(Ⅰ)求 的最小正周期;
的最小正周期;
(Ⅱ)设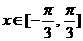 ,求
,求 的值域和单调递增区间.
的值域和单调递增区间.
解:(Ⅰ)∵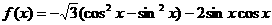
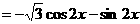
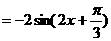 . ……………3分
. ……………3分
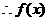 的最小正周期为
的最小正周期为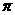 .
………………… 5分
.
………………… 5分
(Ⅱ)∵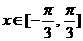 ,
, 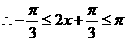 ,
, 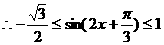 .
.
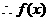 的值域为
的值域为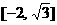 . ……………… 10分
. ……………… 10分
 当
当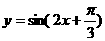 递减时,
递减时, 递增.
递增.
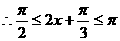 ,即
,即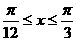 .
.
故 的递增区间为
的递增区间为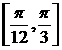 .
……………………12分
.
……………………12分
2009年联考题
9.(2009枣庄一模)已知函数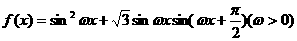
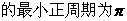
(1)求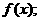
(2)当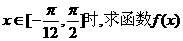 的值域。
的值域。
解:(1)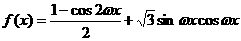 2分
2分
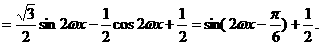 4分
4分
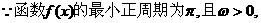

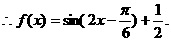 6分
6分
(2)
根据正弦函数的图象可得:
当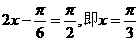 时,
时,
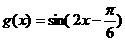 取最大值1 8分
取最大值1 8分
当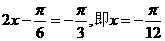 时
时
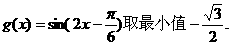 10分
10分
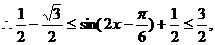
即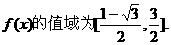 12分
12分
8.(2009汕头一模)己知函数f(x)=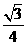 sin x一
sin x一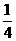 cos x。
cos x。
(1)若cosx=-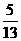 ,x
,x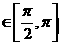 ,求函数f (x)的值;
,求函数f (x)的值;
(2)将函数f(x)的图像向右平移m个单位,使平移后的图像关于原点对称,
若0<m<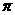 ,试求m的值。
,试求m的值。
解:(1)因为cos=-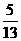 ,x
,x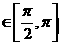 ,所以,sinx=
,所以,sinx=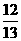
所以,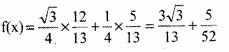
(2)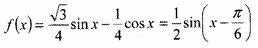 ,
,
所以,把f(x)的图象向右平移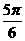 个单位,得到,y=-
个单位,得到,y=-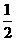 sinx的图象,其图象关于原点对称。
sinx的图象,其图象关于原点对称。
故m=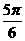
7.(2009日照一模)已知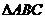 中,角
中,角 的对边分别为
的对边分别为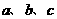 ,且满足
,且满足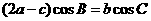 。
。
(I)求角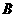 的大小;
的大小;
(Ⅱ)设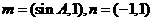 ,求
,求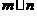 的最小值。
的最小值。
解:(I)由于弦定理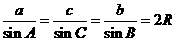 ,
,
有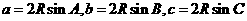
代入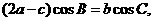 得
得 。
。
……………………………4分
即 。
。
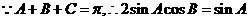 …………………………………6分
…………………………………6分
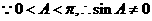
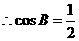 ……………………………………7分
……………………………………7分
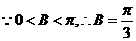 …………………………………8分
…………………………………8分
(Ⅱ)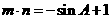 ,
………………………………10分
,
………………………………10分
由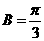 ,得
,得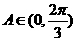 。
…………………………11分
。
…………………………11分
所以,当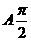 时,
时,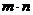 取得最小值为0, ………………………………12分
取得最小值为0, ………………………………12分
6.(2009上海青浦区)已知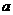 为实数,函数
为实数,函数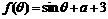 ,
,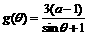 (
(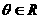 ).
).
(1)若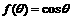 ,试求
,试求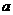 的取值范围;
的取值范围;
(2)若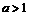 ,求函数
,求函数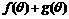 的最小值.
的最小值.
(1)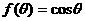 即
即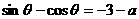 ,又
,又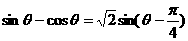 ,2分
,2分
所以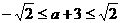 ,从而
,从而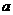 的取值范围是
的取值范围是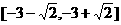 . ……5分
. ……5分
(2)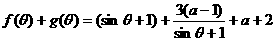 ,令
,令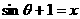 ,则
,则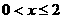 ,因为
,因为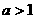 ,所以
,所以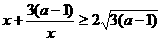 ,当且仅当
,当且仅当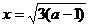 时,等号成立,8分
时,等号成立,8分
由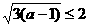 解得
解得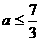 ,所以当
,所以当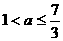 时,函数
时,函数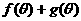 的最小值是
的最小值是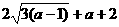 ;
……11分
;
……11分
下面求当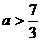 时,函数
时,函数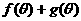 的最小值.
的最小值.
当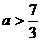 时,
时,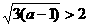 ,函数
,函数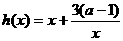 在
在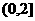 上为减函数.所以函数
上为减函数.所以函数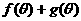 的最小值为
的最小值为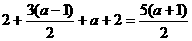 .
.
[当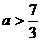 时,函数
时,函数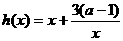 在
在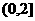 上为减函数的证明:任取
上为减函数的证明:任取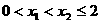 ,
,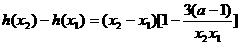 ,因为
,因为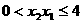 ,
,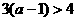 ,所以
,所以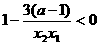 ,
,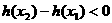 ,由单调性的定义函数
,由单调性的定义函数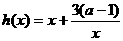 在
在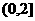 上为减函数.]
上为减函数.]
于是,当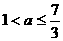 时,函数
时,函数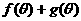 的最小值是
的最小值是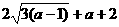 ;当
;当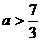 时,函数
时,函数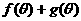 的最小值
的最小值 .
……15分
.
……15分
5.(2009闵行三中模拟)已知函数 是R上的奇函数,且最小正周期为π。
是R上的奇函数,且最小正周期为π。
(1)求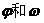 的值;
的值;
(2)求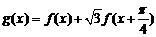 取最小值时的x的集合。
取最小值时的x的集合。
解:(1) 函数最小正周期为
函数最小正周期为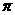 ,且
,且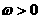 ,
,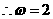 ………2分
………2分
又
 是奇函数,且
是奇函数,且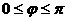 ,由f(0)=0得
,由f(0)=0得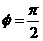 ……………5分
……………5分
(2) 由(1)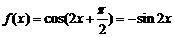 。 ………………………………………6分
。 ………………………………………6分
所以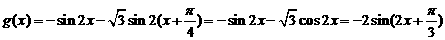 ,……10分
,……10分
当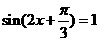 时,g(x)取得最小值,此时
时,g(x)取得最小值,此时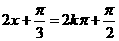 ,
,
解得 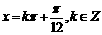 ……………………………………………12分
……………………………………………12分
所以,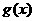 取得最小值时
取得最小值时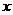 的集合为
的集合为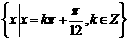 ………………14分
………………14分
4.(2009上海八校联考)已知函数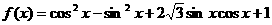 .
.
(1)求 的最小正周期,并求
的最小正周期,并求 的最小值;
的最小值;
(2)若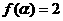 ,且
,且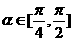 ,求
,求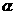 的值
的值
解:(1)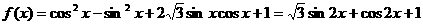
=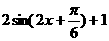 .
.  4分
4分
因此 的最小正周期为
的最小正周期为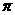 ,最小值为
,最小值为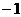 .
.  6分
6分
(2) 由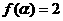 得
得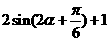 =2,即
=2,即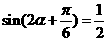 ,
,
而由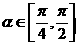 ,得
,得 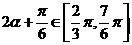 .
.  9分
9分
故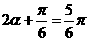 , 解得
, 解得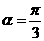 .
.  12分
12分
3.(2009茂名一模)设函数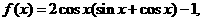 将函数
将函数 的图象向左平移
的图象向左平移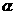 个单位,得到函数
个单位,得到函数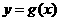 的图象。
的图象。
(1)求函数 的最小正周期;
的最小正周期;
(2)若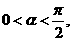 且
且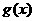 是偶函数,求
是偶函数,求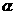 的值。
的值。
解:

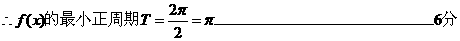
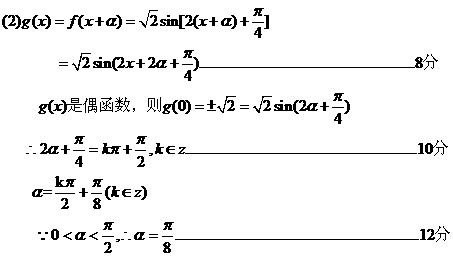
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com