
题目列表(包括答案和解析)
5.(2009四川卷理)已知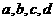 为实数,且
为实数,且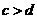 。则“
。则“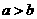 ”是“
”是“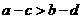 ”的
”的
A. 充分而不必要条件 B. 必要而不充分条件
C.充要条件 D. 既不充分也不必要条件
[考点定位]本小题考查不等式的性质、简单逻辑,基础题。(同文7)
答案 B
解析 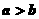 推不出
推不出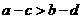 ;但
;但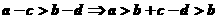 ,故选择B。
,故选择B。
解析2:令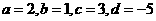 ,则
,则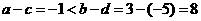 ;由
;由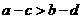 可得,
可得,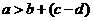 因为
因为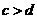 ,则
,则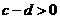 ,所以
,所以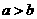 。故“
。故“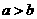 ”是“
”是“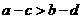 ”的必要而不充分条件。
”的必要而不充分条件。
4.(2009天津卷理)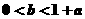 ,若关于x 的不等式
,若关于x 的不等式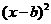 >
>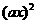 的解集中的整数恰有3个,则
的解集中的整数恰有3个,则
A. B.
B.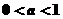 C.
C.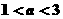 D.
D.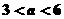
答案 C
3.(2009四川卷文)已知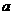 ,
,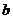 ,
,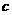 ,
,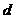 为实数,且
为实数,且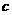 >
>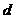 .则“
.则“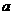 >
>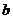 ”是“
”是“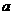 -
-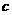 >
>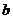 -
-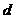 ”的
”的
A. 充分而不必要条件 B. 必要而不充分条件
C. 充要条件 D. 既不充分也不必要条件
答案 B
解析
显然,充分性不成立.又,若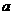 -
-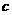 >
>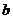 -
-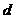 和
和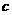 >
>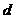 都成立,则同向不等式相加得
都成立,则同向不等式相加得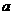 >
>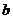
即由“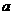 -
-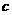 >
>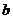 -
-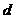 ”
” “
“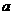 >
>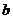 ”
”
2.(2009安徽卷文)“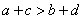 ”是“
”是“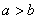 且
且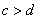 ”的
”的
A. 必要不充分条件 B. 充分不必要条件
C. 充分必要条件 D. 既不充分也不必要条件
答案 A
解析 易得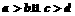 时必有
时必有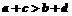 .若
.若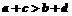 时,则可能有
时,则可能有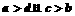 ,选A。
,选A。
1.(2009安徽卷理)下列选项中,p是q的必要不充分条件的是
A.p: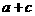 >b+d , q:
>b+d , q: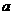 >b且c>d
>b且c>d
B.p:a>1,b>1 q: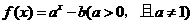 的图像不过第二象限
的图像不过第二象限
C.p: x=1, q: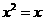
D.p:a>1,
q: 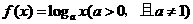 在
在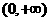 上为增函数
上为增函数
答案 A
解析 由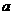 >b且c>d
>b且c>d
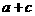 >b+d,而由
>b+d,而由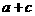 >b+d
>b+d 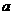 >b且c>d,可举反例。选A。
>b且c>d,可举反例。选A。
3.(2010湖北理) 15.设a>0,b>0,称
15.设a>0,b>0,称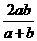 为a,b的调和平均数。如图,C为线段AB上的点,且AC=a,CB=b,O为AB中点,以AB为直径做半圆。过点C作AB的垂线交半圆于D。连结OD,AD,BD。过点C作OD的垂线,垂足为E。则图中线段OD的长度是a,b的算术平均数,线段 的长度是a,b的几何平均数,线段 的长度是a,b的调和平均数。
为a,b的调和平均数。如图,C为线段AB上的点,且AC=a,CB=b,O为AB中点,以AB为直径做半圆。过点C作AB的垂线交半圆于D。连结OD,AD,BD。过点C作OD的垂线,垂足为E。则图中线段OD的长度是a,b的算术平均数,线段 的长度是a,b的几何平均数,线段 的长度是a,b的调和平均数。
[答案]CD DE
[解析]在Rt△ADB中DC为高,则由射影定理可得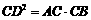 ,故
,故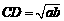 ,即CD长度为a,b的几何平均数,将OC=
,即CD长度为a,b的几何平均数,将OC=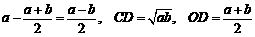 代入
代入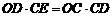 可得
可得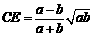 故
故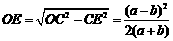 ,所以ED=OD-OE=
,所以ED=OD-OE=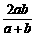 ,故DE的长度为a,b的调和平均数.
,故DE的长度为a,b的调和平均数.
2009年高考题
第一节 简单不等式及其解法
2.(2010广东文)19.(本题满分12分)
某营养师要求为某个儿童预订午餐和晚餐.已知一个单位的午餐含12个单位的碳水化合物,6个单位的蛋白质和6个单位的维生素C;一个单位的晚餐含8个单位的碳水化合物,6个单位的蛋白质和10个单位的维生素C.另外,该儿童这两餐需要的营状中至少含64个单位的碳水化合物和42个单位的蛋白质和54个单位的维生素C.
如果一个单位的午餐、晚餐的费用分别是2.5元和4元,那么要满足上述的营养要求,并且花费最少,应当为该儿童分别预订多少个单位的午餐和晚餐?
 解:设为该儿童分别预订
解:设为该儿童分别预订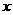 个单位的午餐和
个单位的午餐和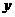 个单位的晚餐,设费用为F,则F
个单位的晚餐,设费用为F,则F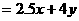 ,由题意知:
,由题意知:
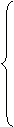
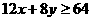
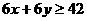
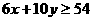
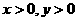
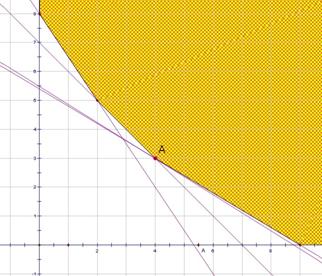
画出可行域:
变换目标函数: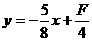

1.(2010广东理)19.(本小题满分12分)
某营养师要为某个儿童预定午餐和晚餐。已知一个单位的午餐含12个单位的碳水化合物6个单位蛋白质和6个单位的维生素C;一个单位的晚餐含8个单位的碳水化合物,6个单位的蛋白质和10个单位的维生素C.另外,该儿童这两餐需要的营养中至少含64个单位的碳水化合物,42个单位的蛋白质和54个单位的维生素C.
如果一个单位的午餐、晚餐的费用分别是2.5元和4元,那么要满足上述的营养要求,并且花费最少,应当为该儿童分别预定多少个单位的午餐和晚餐?
解:设该儿童分别预订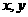 个单位的午餐和晚餐,共花费
个单位的午餐和晚餐,共花费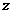 元,则
元,则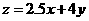 。
。
 可行域为
可行域为
 12 x+8 y ≥64
12 x+8 y ≥64
6 x+6 y ≥42
6 x+10 y ≥54
x≥0, x∈N
y≥0, y∈N
即
 3 x+2 y ≥16
3 x+2 y ≥16
x+ y ≥7
3 x+5 y ≥27
x≥0, x∈N
y≥0, y∈N
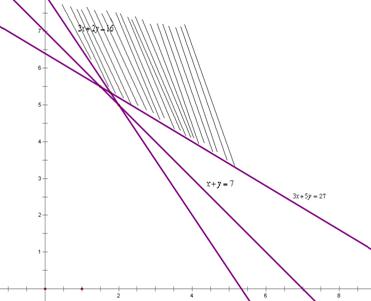
作出可行域如图所示:
经试验发现,当x=4,y=3
时,花费最少,为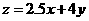 =2.5×4+4×3=22元.
=2.5×4+4×3=22元.
17.(2010江苏卷)12、设实数x,y满足3≤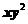 ≤8,4≤
≤8,4≤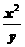 ≤9,则
≤9,则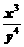 的最大值是 。。
的最大值是 。。
[答案] 27
[解析]考查不等式的基本性质,等价转化思想。
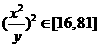 ,
,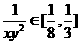 ,
,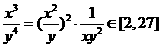 ,
,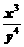 的最大值是27。
的最大值是27。
16.(2010湖北理) 15.设a>0,b>0,称
15.设a>0,b>0,称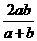 为a,b的调和平均数。如图,C为线段AB上的点,且AC=a,CB=b,O为AB中点,以AB为直径做半圆。过点C作AB的垂线交半圆于D。连结OD,AD,BD。过点C作OD的垂线,垂足为E。则图中线段OD的长度是a,b的算术平均数,线段 的长度是a,b的几何平均数,线段 的长度是a,b的调和平均数。
为a,b的调和平均数。如图,C为线段AB上的点,且AC=a,CB=b,O为AB中点,以AB为直径做半圆。过点C作AB的垂线交半圆于D。连结OD,AD,BD。过点C作OD的垂线,垂足为E。则图中线段OD的长度是a,b的算术平均数,线段 的长度是a,b的几何平均数,线段 的长度是a,b的调和平均数。
[答案]CD DE
[解析]在Rt△ADB中DC为高,则由射影定理可得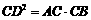 ,故
,故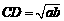 ,即CD长度为a,b的几何平均数,将OC=
,即CD长度为a,b的几何平均数,将OC=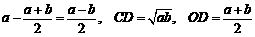 代入
代入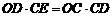 可得
可得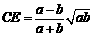 故
故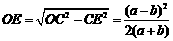 ,所以ED=OD-OE=
,所以ED=OD-OE=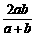 ,故DE的长度为a,b的调和平均数.
,故DE的长度为a,b的调和平均数.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com