
题目列表(包括答案和解析)
6.(2006上海)若关于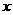 的不等式
的不等式 ≤
≤ +4的解集是M,则对任意实常数
+4的解集是M,则对任意实常数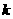 ,总
,总
有( )
A.2∈M,0∈M; B.2 M,0
M,0 M; C.2∈M,0
M; C.2∈M,0 M; D.2
M; D.2 M,0∈M.
M,0∈M.
答案 A
解析
方法1:代入判断法,将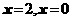 分别代入不等式中,判断关于
分别代入不等式中,判断关于 的不等式解集是否为
的不等式解集是否为 ;
;
方法2:求出不等式的解集: ≤
≤ +4
+4
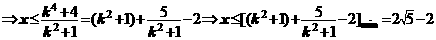 ;
;
5.(2006陕西)设x,y为正数, 则(x+y)( + )的最小值为( )
A. 6 B.9 C.12 D.15
答案 B
解析
x,y为正数,(x+y)( )≥
)≥ ≥9,选B.
≥9,选B.
4.(2006陕西)已知不等式(x+y)( + )≥9对任意正实数x,y恒成立,则正实数a的最小值为( )
A.2 B.4 C.6 D.8
答案 B
解析
不等式(x+y)( )≥9对任意正实数x,y恒成立,则
)≥9对任意正实数x,y恒成立,则 ≥
≥ ≥9,∴
≥9,∴  ≥2或
≥2或 ≤-4(舍去),所以正实数a的最小值为4,选B.
≤-4(舍去),所以正实数a的最小值为4,选B.
3.(2006江苏)设a、b、c是互不相等的正数,则下列等式中不恒成立的是
A. B.
B.
C.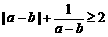 D.
D.
[思路点拨]本题主要考查.不等式恒成立的条件,由于给出的是不完全提干,必须结合选择支,才能得出正确的结论。
答案 C
解析 运用排除法,C选项 ,当a-b<0时不成立。
,当a-b<0时不成立。
[解后反思]运用公式一定要注意公式成立的条件
如果
如果a,b是正数,那么
2.(2007北京)如果正数 满足
满足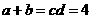 ,那么( A )
,那么( A )
A. ,且等号成立时
,且等号成立时 的取值唯一
的取值唯一
B. ,且等号成立时
,且等号成立时 的取值唯一
的取值唯一
C. ,且等号成立时
,且等号成立时 的取值不唯一
的取值不唯一
D. ,且等号成立时
,且等号成立时 的取值不唯一
的取值不唯一
答案 A
1.(2008陕西)“ ”是“对任意的正数
”是“对任意的正数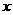 ,
, ”的( )
”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
答案 A
30.(2007湖北)已知m,n为正整数.
(Ⅰ)用数学归纳法证明:当x>-1时,(1+x)m≥1+mx;
(Ⅱ)对于n≥6,已知 ,求证
,求证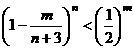 ,m=1,1,2…,n;
,m=1,1,2…,n;
(Ⅲ)求出满足等式3n+4m+…+(n+2)m=(n+3)n的所有正整数n.
解:(Ⅰ)证:当x=0或m=1时,原不等式中等号显然成立,下用数学归纳法证明:
当x>-1,且x≠0时,m≥2,(1+x)m>1+mx. 1
(i)当m=2时,左边=1+2x+x2,右边=1+2x,因为x≠0,所以x2>0,即左边>右边,不等式①成立;
(ii)假设当m=k(k≥2)时,不等式①成立,即(1+x)k>1+kx,则当m=k+1时,因为x>-1,所以1+x>0.又因为x≠0,k≥2,所以kx2>0.
于是在不等式(1+x)k>1+kx两边同乘以1+x得
(1+x)k·(1+x)>(1+kx)(1+x)=1+(k+1)x+kx2>1+(k+1)x,
所以(1+x)k+1>1+(k+1)x,即当m=k+1时,不等式①也成立.
综上所述,所证不等式成立.
(Ⅱ)证:当
而由(Ⅰ),

(Ⅲ)解:假设存在正整数 成立,
成立,
即有( )+
)+ =1. ②
=1. ②
又由(Ⅱ)可得
( )+
)+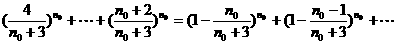
+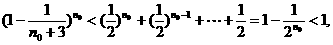 与②式矛盾,
与②式矛盾,
故当n≥6时,不存在满足该等式的正整数n.
故只需要讨论n=1,2,3,4,5的情形;
当n=1时,3≠4,等式不成立;
当n=2时,32+42=52,等式成立;
当n=3时,33+43+53=63,等式成立;
当n=4时,34+44+54+64为偶数,而74为奇数,故34+44+54+64≠74,等式不成立;
当n=5时,同n=4的情形可分析出,等式不成立.
综上,所求的n只有n=2,3.
第二节 基本不等式
29.(2007北京)记关于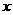 的不等式
的不等式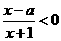 的解集为
的解集为 ,不等式
,不等式 的解集为
的解集为 .
.
(I)若 ,求
,求 ;
;
(II)若 ,求正数
,求正数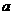 的取值范围.
的取值范围.
解:(I)由 ,得
,得 .
.
(II) .
.
由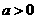 ,得
,得 ,又
,又 ,所以
,所以 ,
,
即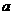 的取值范围是
的取值范围是 .
.
28.(2006上海)不等式 的解集是
.
的解集是
.
答案  .
.
解析 应用结论:  .不等式
.不等式
 等价于(1-2x)(x+1)>0,也就是
等价于(1-2x)(x+1)>0,也就是  ,所以
,所以
 ,从而应填
,从而应填
 .
.
27.(2006浙江)不等式 的解集是 。.
的解集是 。.
答案
 x<-1或x>2
x<-1或x>2
解析
 Û(x+1)(x-2)>0Ûx<-1或x>2.
Û(x+1)(x-2)>0Ûx<-1或x>2.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com