
题目列表(包括答案和解析)
2.(2009山东卷文)若函数f(x)=a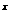 -x-a(a>0且a
-x-a(a>0且a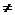 1)有两个零点,则实数a的取值范围是 .
1)有两个零点,则实数a的取值范围是 .
答案 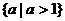
解析 设函数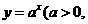 且
且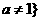 和函数
和函数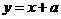 ,则函数f(x)=a
,则函数f(x)=a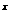 -x-a(a>0且a
-x-a(a>0且a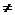 1)有两个零点, 就是函数
1)有两个零点, 就是函数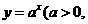 且
且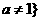 与函数
与函数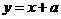 有两个交点,由图象可知当
有两个交点,由图象可知当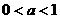 时两函数只有一个交点,不符合,当
时两函数只有一个交点,不符合,当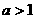 时,因为函数
时,因为函数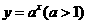 的图象过点(0,1),而直线
的图象过点(0,1),而直线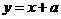 所过的点(0,a)一定在点(0,1)的上方,所以一定有两个交点.所以实数a的取值范围是
所过的点(0,a)一定在点(0,1)的上方,所以一定有两个交点.所以实数a的取值范围是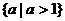 .
.
[命题立意]:本题考查了指数函数的图象与直线的位置关系,隐含着对指数函数的性质的考查,根据其底数的不同取值范围而分别画出函数的图象进行解答
1.(2009福建卷文)若函数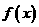 的零点与
的零点与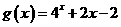 的零点之差的绝对值不超过0.25, 则
的零点之差的绝对值不超过0.25, 则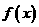 可以是
可以是
A. 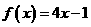 B.
B.
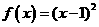
C. 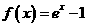 D.
D.
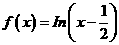
答案 A
解析 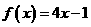 的零点为x=
的零点为x=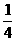 ,
,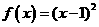 的零点为x=1,
的零点为x=1, 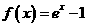 的零点为x=0,
的零点为x=0, 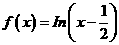 的零点为x=
的零点为x=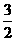 .现在我们来估算
.现在我们来估算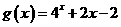 的零点,因为g(0)= -1,g(
的零点,因为g(0)= -1,g(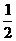 )=1,所以g(x)的零点x
)=1,所以g(x)的零点x (0,
(0,
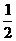 ),又函数
),又函数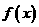 的零点与
的零点与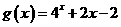 的零点之差的绝对值不超过0.25,只有
的零点之差的绝对值不超过0.25,只有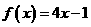 的零点适合,故选A。
的零点适合,故选A。
2.(2010湖北文)19.(本小题满分12分)
已知某地今年年初拥有居民住房的总面积为a(单位:m2),其中有部分旧住房需要拆除。当地有关部门决定每年以当年年初住房面积的10%建设新住房,同事也拆除面积为b(单位:m2)的旧住房。
(Ⅰ)分别写出第一年末和第二年末的实际住房面积的表达式:
(Ⅱ)如果第五年末该地的住房面积正好比今年年初的住房面积增加了30%,则每年拆除的旧住房面积b是多少?(计算时取1.15=1.6)

2009年高考题
1.(2010福建文)21.(本小题满分12分)
某港口 要将一件重要物品用小艇送到一艘正在航行的轮船上,在小艇出发时,轮船位于港口
要将一件重要物品用小艇送到一艘正在航行的轮船上,在小艇出发时,轮船位于港口 北偏西30°且与该港口相距20海里的
北偏西30°且与该港口相距20海里的 处,并正以30海里/小时的航行速度沿正东方向匀速行驶。假设该小艇沿直线方向以
处,并正以30海里/小时的航行速度沿正东方向匀速行驶。假设该小艇沿直线方向以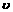 海里/小时的航行速度匀速行驶,经过
海里/小时的航行速度匀速行驶,经过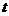 小时与轮船相遇。
小时与轮船相遇。
(Ⅰ)若希望相遇时小艇的航行距离最小,则小艇航行速度的大小应为多少?
(Ⅱ)为保证小艇在30分钟内(含30分钟)能与轮船相遇,试确定小艇航行速度的最小值;
(Ⅲ)是否存在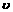 ,使得小艇以
,使得小艇以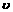 海里/小时的航行速度行驶,总能有两种不同的航行方向与轮船相遇?若存在,试确定
海里/小时的航行速度行驶,总能有两种不同的航行方向与轮船相遇?若存在,试确定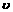 的取值范围;若不存在,请说明理由。
的取值范围;若不存在,请说明理由。


9.(2010江苏卷)11、已知函数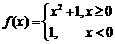 ,则满足不等式
,则满足不等式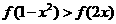 的x的范围是_____。
的x的范围是_____。
[解析] 考查分段函数的单调性。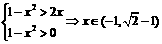
8.(2010广东文数)
7.(2010天津理数)(16)设函数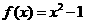 ,对任意
,对任意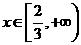 ,
,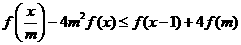 恒成立,则实数
恒成立,则实数 的取值范围是 .
的取值范围是 .
[解析]本题主要考查函数恒成立问题的基本解法,属于难题。
依据题意得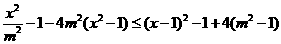 在
在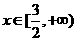 上恒定成立,即
上恒定成立,即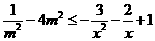 在
在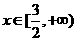 上恒成立。
上恒成立。
当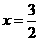 时函数
时函数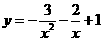 取得最小值
取得最小值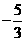 ,所以
,所以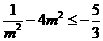 ,即
,即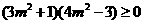 ,解得
,解得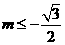 或
或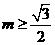
[温馨提示]本题是较为典型的恒成立问题,解决恒成立问题通常可以利用分离变量转化为最值的方法求解
6.(2010浙江文)(16) 某商家一月份至五月份累计销售额达3860万元,预测六月份销售额为500万元,七月份销售额比六月份递增x%,八月份销售额比七月份递增x%,九、十月份销售总额与七、八月份销售总额相等,若一月至十月份销售总额至少至少达7000万元,则,x 的最小值 。
答案 20
5.(2010天津文)(16)设函数f(x)=x-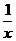 ,对任意x
,对任意x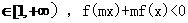 恒成立,则实数m的取值范围是________
恒成立,则实数m的取值范围是________
[答案]m<-1
[解析]本题主要考查了恒成立问题的基本解法及分类讨论思想,属于难题。
已知f(x)为增函数且m≠0
若m>0,由复合函数的单调性可知f(mx)和mf(x)均为增函数,此时不符合题意。
M<0,时有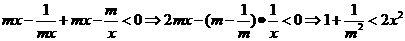 因为
因为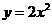 在
在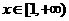 上的最小值为2,所以1+
上的最小值为2,所以1+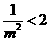 即
即 >1,解得m<-1.
>1,解得m<-1.
[温馨提示]本题是较为典型的恒成立问题,解决恒成立问题通常可以利用分离变量转化为最值的方法求解。
4.(2010重庆理)(15)已知函数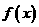 满足:
满足: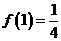 ,
,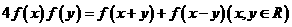 ,则
,则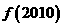 =_____________.
=_____________.
解析:取x=1 y=0得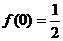
法一:通过计算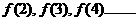 ,寻得周期为6
,寻得周期为6
法二:取x=n y=1,有f(n)=f(n+1)+f(n-1),同理f(n+1)=f(n+2)+f(n)
联立得f(n+2)= -f(n-1) 所以T=6
故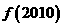 =f(0)=
=f(0)= 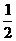
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com