
题目列表(包括答案和解析)
21.若函数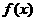 对定义域中任一
对定义域中任一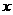 均满足
均满足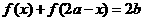 ,则函数
,则函数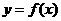 的图像关于点
的图像关于点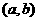 对称。
对称。
(1)已知函数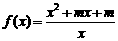 的图像关于点
的图像关于点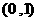 对称,求实数
对称,求实数 的值;
的值;
(2)已知函数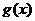 在
在 上的图像关于点
上的图像关于点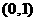 对称,且当
对称,且当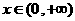 时,
时,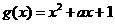 ,求函数
,求函数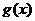 在
在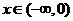 上的解析式;
上的解析式;
(3)在(1)、(2)的条件下,若对实数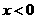 及
及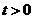 ,恒有
,恒有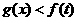 ,求实数
,求实数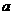 的取值范围。
的取值范围。
解:(1)由题设可得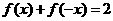 ,解得
,解得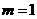 ;
;
(2)当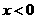 时,
时,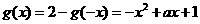 ;
;
(3)由(1)得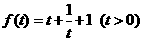 , 其最小值为
, 其最小值为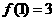 ,
, 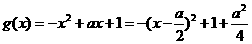 ,
,
当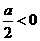 ,即
,即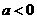 时,
时,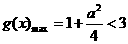 ,得
,得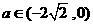 ,
,
① ②当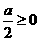 ,即
,即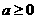 时,
时,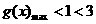 ,得
,得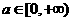 ,由①、②得
,由①、②得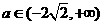 。
。
40.已知函数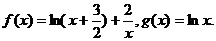
(1)求函数f(x)是单调区间;
(2)如果关于x的方程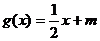 有实数根,求实数
有实数根,求实数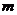 的取值集合;
的取值集合;
(3)是否存在正数k,使得关于x的方程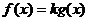 有两个不相等的实数根?如果存在,求k满足的条件;如果不存在,说明理由.
有两个不相等的实数根?如果存在,求k满足的条件;如果不存在,说明理由.
解:(1)函数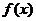 的定义域是
的定义域是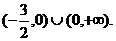
对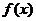 求导得
求导得
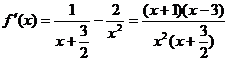 …………(2分)
…………(2分)
由
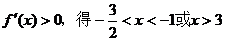
由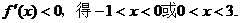
因此
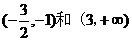 是函数
是函数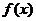 的增区间;
的增区间;
(-1,0)和(0,3)是函数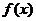 的减区间 ………………(5分)
的减区间 ………………(5分)
(2)[解法一]:因为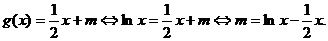
所以实数m的取值范围就是函数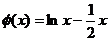 的值域 …………(6分)
的值域 …………(6分)
对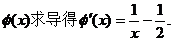
令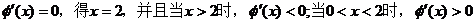
∴当x=2时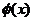 取得最大值,且
取得最大值,且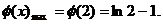
又当x无限趋近于0时,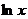 无限趋近于
无限趋近于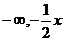 无限趋近于0,
无限趋近于0,
进而有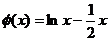 无限趋近于-∞.
无限趋近于-∞.
因此函数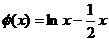 的值域是
的值域是 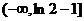
即实数m的取值范围是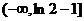 ………………(9分)
………………(9分)
[解法二]:方程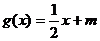 有实数根等价于直线
有实数根等价于直线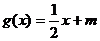 与曲线y=lnx有公共点,并且当直线
与曲线y=lnx有公共点,并且当直线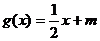 与曲线y=lnx相切时,m取得最大值. ……(6分)
与曲线y=lnx相切时,m取得最大值. ……(6分)
设直线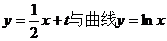 相切,切点为
相切,切点为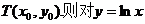 求导得
求导得
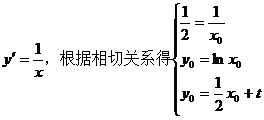
解得 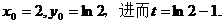
所以m的最大值是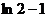 。而且易知当
。而且易知当 与曲线y=lnx总有公共点。
与曲线y=lnx总有公共点。
因此实数m的取值集合是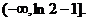 ………………(9分)
………………(9分)
(3)结论:这样的正数k不存在。 ………………(10分)
下面采用反证法来证明:假设存在正数k,使得关于x的方程
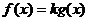 有
有 两个不相等的实数根
两个不相等的实数根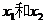 ,则
,则
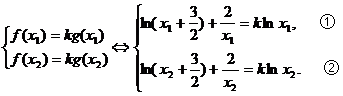 …………(11分)
…………(11分)
根据对数函数定义域知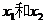 都是正数。
都是正数。
又由(1)可知,当
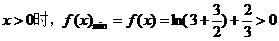
∴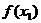 =
=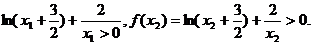
再由k>0,可得
由于 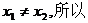 不妨设
不妨设 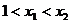
由①和②可得 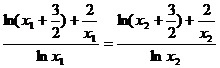
利用比例性质得 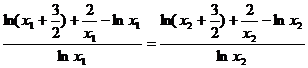
即 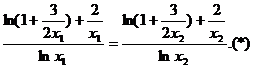 …………(13分)
…………(13分)
由于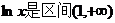 上的恒正增函数,且
上的恒正增函数,且 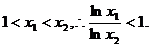
又由于 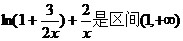 上的恒正减函数,且
上的恒正减函数,且 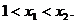
∴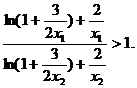
∴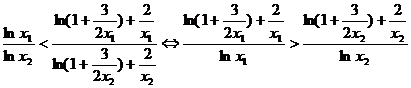
这与(*)式矛盾。
因此满足条件的正数k不存在 ……………………(14分)
39. 已知抛物线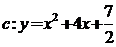 ,过C上点M,且与M处的切线垂直的直线称为C在点M的法线。
,过C上点M,且与M处的切线垂直的直线称为C在点M的法线。
⑴若C在点M的法线的斜率为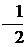 ,求点M的坐标(
,求点M的坐标(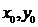 );
);
⑵设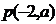 为C对称轴上的一点,在C上是否存在点,使得C在该点的法线通过点P?若有,求出这些点,以及C在这些点的法线方程;若没有,请说明理由。
为C对称轴上的一点,在C上是否存在点,使得C在该点的法线通过点P?若有,求出这些点,以及C在这些点的法线方程;若没有,请说明理由。
解(1)函数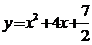 的导数
的导数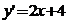 上点
上点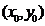 处切线的斜率
处切线的斜率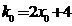 ,因为过点
,因为过点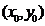 的法线斜率为
的法线斜率为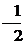 ,所以
,所以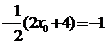 ,解得
,解得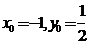 ,故点M的坐标为
,故点M的坐标为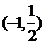 。
。
(2)设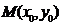 为C上一点,
为C上一点,
①若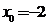 ,则C上点
,则C上点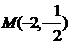 处的切线斜率
处的切线斜率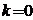 ,过点
,过点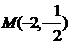 的法线方程为
的法线方程为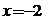 ,此法线过点
,此法线过点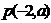 ;
;
②若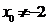 ,则过点
,则过点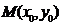 的法线方程为:
的法线方程为: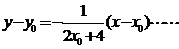 ①
①
若法线过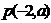 ,则
,则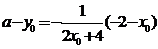 ,即
,即 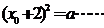 ②
②
若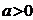 ,则
,则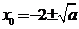 ,从而
,从而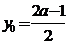 ,将上式代入①,
,将上式代入①,
化简得: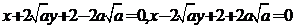 ,
,
若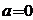 与
与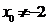 矛盾,若
矛盾,若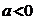 ,则②式无解。
,则②式无解。
综上,当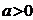 时,在C上有三点
时,在C上有三点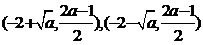 及
及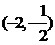 ,在这三点的法线过
,在这三点的法线过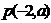 ,其方程分别是:
,其方程分别是:
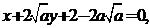
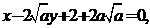
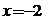 。
。
当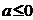 时,在C上有一点
时,在C上有一点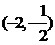 ,在这点的法线过点
,在这点的法线过点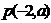 ,其方程为:
,其方程为: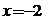 。
。
38.设无穷数列{an}具有以下性质:①a1=1;②当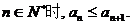
(Ⅰ)请给出一个具有这种性质的无穷数列,使得不等式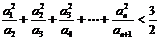 对于任意的
对于任意的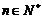 都成立,并对你给出的结果进行验证(或证明);
都成立,并对你给出的结果进行验证(或证明);
(Ⅱ)若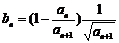 ,其中
,其中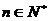 ,且记数列{bn}的前n项和Bn,证明:
,且记数列{bn}的前n项和Bn,证明: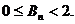
解:(Ⅰ)令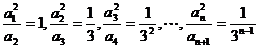 ,
,
则无穷数列{an}可由a1 =
1,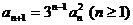 给出.
给出.
显然,该数列满足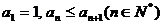 ,且
,且
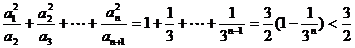 ……………………6分
……………………6分
(Ⅱ)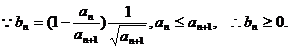
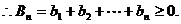 ………………………………………………8分
………………………………………………8分
又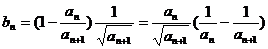
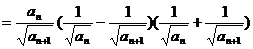
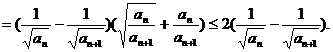
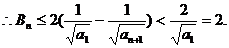
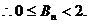
37.已知圆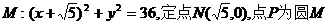 上的动点,点Q在NP上,点G在MP上,且满足
上的动点,点Q在NP上,点G在MP上,且满足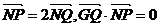 .
.
(1)求点G的轨迹C的方程;
(2)过点(2,0)作直线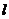 ,与曲线C交于A、B两点,O是坐标原点,设
,与曲线C交于A、B两点,O是坐标原点,设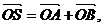 是否存在这样的直线
是否存在这样的直线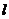 ,使四边形OASB的对角线相等(即|OS|=|AB|)?若存在,求出直线
,使四边形OASB的对角线相等(即|OS|=|AB|)?若存在,求出直线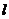 的方程;若不存在,试说明理由.
的方程;若不存在,试说明理由.
解:(1)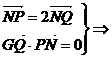 Q为PN的中点且GQ⊥PN
Q为PN的中点且GQ⊥PN
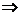 GQ为PN的中垂线
GQ为PN的中垂线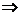 |PG|=|GN|
|PG|=|GN|
∴|GN|+|GM|=|MP|=6,故G点的轨迹是以M、N为焦点的椭圆,其长半轴长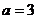 ,半焦距
,半焦距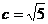 ,∴短半轴长b=2,∴点G的轨迹方程是
,∴短半轴长b=2,∴点G的轨迹方程是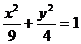
(2)因为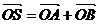 ,所以四边形OASB为平行四边形
,所以四边形OASB为平行四边形
若存在l使得|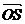 |=|
|=|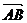 |,则四边形OASB为矩形
|,则四边形OASB为矩形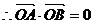
若l的斜率不存在,直线l的方程为x=2,由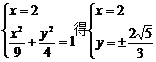
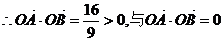 矛盾,故l的斜率存在.
矛盾,故l的斜率存在.
设l的方程为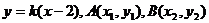
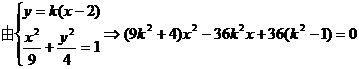
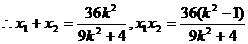 ①
①
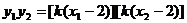
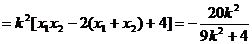 ②
②
把①、②代入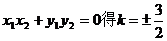
∴存在直线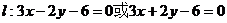 使得四边形OASB的对角线相等.
使得四边形OASB的对角线相等.
35.已知等差数列{an}的首项a1=1,公差d>0,且第二项、第五项、第十四项分别是一个等比数列的第二项、第三项、第四项.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设bn=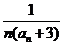 (n∈N*),Sn=b1+b2+…+bn,是否存在最大的整数t,使得任意的n均有Sn>
(n∈N*),Sn=b1+b2+…+bn,是否存在最大的整数t,使得任意的n均有Sn>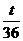 总成立?若存在,求出t;若不存在,请说明理由.
总成立?若存在,求出t;若不存在,请说明理由.
解:(Ⅰ)由题意得(a1+d)(a1+13d)=(a1+4d)2, ……………………… 2 分
整理得2a1d=d2.
∵a1=1,解得(d=0舍),d=2. ………………………………………… 4 分
∴an=2n-1(n∈N*). …………………………………………………… 6 分
(Ⅱ)bn=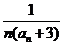 =
=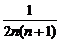 =
=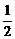 (
(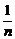 -
-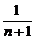 ),
),
∴Sn=b1+b2+…+bn=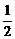 [(1-
[(1-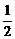 )+(
)+(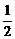 -
-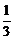 )+…+(
)+…+(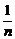 -
-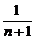 )]
)]
=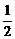 (1-
(1-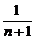 )=
)=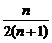 . …………………………………… 10 分
. …………………………………… 10 分
假设存在整数t满足Sn>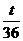 总成立.
总成立.
又Sn+1-Sn=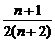 -
-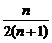 =
=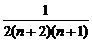 >0,
>0,
∴数列{Sn}是单调递增的. ……………………………………………… 12 分
∴S1=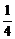 为Sn的最小值,故
为Sn的最小值,故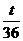 <
<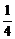 ,即t<9.
,即t<9.
又∵t∈N*,
∴适合条件的t的最大值为8. ………………………………………… 14 分
36 已知数列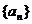 满足:
满足: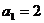 ,
,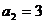 ,
,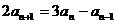
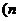 ≥
≥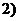 .
.
(Ⅰ)求数列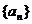 的通项公式
的通项公式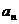 ;
;
(Ⅱ)求使不等式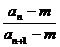 <
<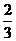 成立的所有正整数
成立的所有正整数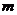 、
、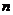 的值.
的值.
解 (Ⅰ)由2 an+1 = 3an-an-1(n≥2),得 2(an+1-an)= an-an-1,
∴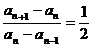 ,因此数列{ an-an-1 }是以a2-a1 = 1为首项,
,因此数列{ an-an-1 }是以a2-a1 = 1为首项,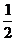 为公比的等比数列,
为公比的等比数列,
∴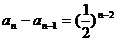 ,……………………………………………………………………………………4分
,……………………………………………………………………………………4分
于是 an =(an-an-1)+(an-1-an-2)+ … +(a2-a1)+ a1
=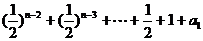 =
=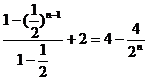 . ………………………………………6分
. ………………………………………6分
(Ⅱ)由不等式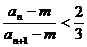 ,得
,得 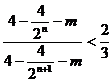 ,
,
∴ 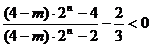 ,即
,即 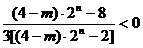 ,………………………………………………8分
,………………………………………………8分
所以 2<(4-m)· 2n <8. ∵ 2n为正偶数,4-m为整数,
∴ (4-m)· 2n = 4,或 (4-m)· 2n = 6,
∴ 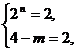 或
或 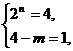 或
或 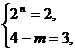 或
或 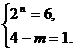
解得 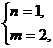 或
或 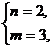 或
或 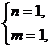 或
或 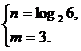
经检验使不等式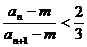 成立的所有正整数m、n的值为
成立的所有正整数m、n的值为
(m,n)=(1,1)或(2,1)或(3,2).………………………………………………………12分
说明 问题(1)的归纳做法是:由已知可得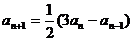 ,
,
∴ 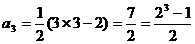 ,
,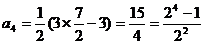 ,
,
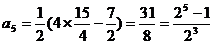 ,……,于是
,……,于是 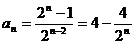 .
.
34.已知函数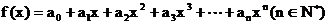 , 且
, 且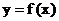
的图象经过点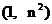 , 数列
, 数列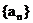 为等差数列.
为等差数列.
(1) 求数列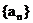 的通项公式
的通项公式
(2) 当n为奇数时, 设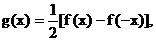
问: 是否存在自然数m和M, 使得不等式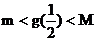 恒成立? 若存在, 求出
恒成立? 若存在, 求出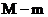 的最
的最
小值; 若不存在, 请说明理由.
解: (1)由题意得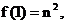 即
即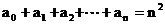 . 令
. 令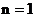 , 则
, 则 令
令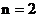 ,
,
则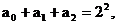
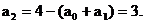 令
令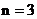 , 则
, 则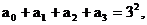
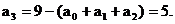 ……(3分)
……(3分)
设等差数列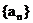 的公差为d, 则
的公差为d, 则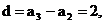
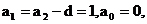 ……(5分)
……(5分)
∴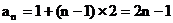 .……(6分)
.……(6分)
(2)由(1)知: 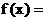
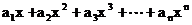 . n为奇数时,
. n为奇数时,
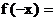
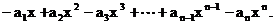 ……(7分)
……(7分)
∴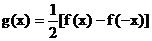
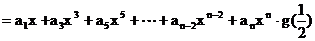
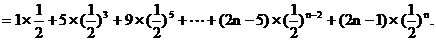 …………①
…………①
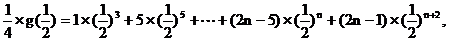 …………②……(9分)
…………②……(9分)
由①-②得: 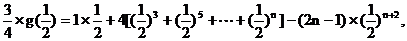
∴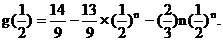 ……(10分)
……(10分)
设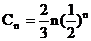 , ∵
, ∵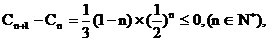
∴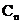 随n的增加而减小.又
随n的增加而减小.又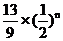 随n的增大而减小, ∴
随n的增大而减小, ∴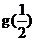 为n的增函数. ……(12分)
为n的增函数. ……(12分)
当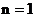 时,
时,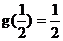 ,而
,而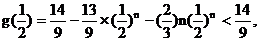 ∴
∴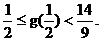 ……(13分)
……(13分)
由此易知: 使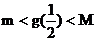 恒成立的m的最大值为0,
恒成立的m的最大值为0,
M的最小值为2, M-m的最小值为2. ……(14分)
33.已知数列{an}有a1=a,a2=p (常数p>0),对任意的正整数n,Sn=a1+a2+…+an,并有Sn满足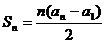 。
。
(1) 求a的值;
(2) 试确定数列{an}是否是等差数列,若是,求出其通项公式,若不是,说明理由;
(3) 对于数列{bn},假如存在一个常数b使得对任意的正整数n都有bn<b,且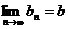 ,则称b为数列{bn}的“上渐进值”,令
,则称b为数列{bn}的“上渐进值”,令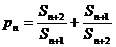 ,求数列{p1+p2+…+pn-2n}的“上渐进值”。
,求数列{p1+p2+…+pn-2n}的“上渐进值”。
解:(1)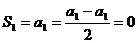 ,即
,即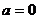
(2)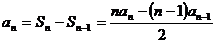
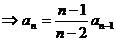
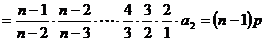
∴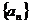 是一个以
是一个以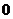 为首项,
为首项,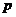 为公差的等差数列。
为公差的等差数列。
(3)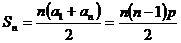 ,
,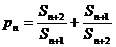
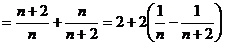
∴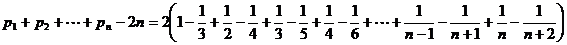
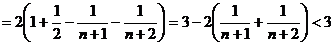
又∵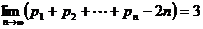 ,∴数列
,∴数列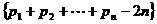 的“上渐近值”为
的“上渐近值”为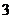 。
。
32.设函数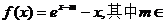 R.
R.
(I)求函数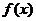 的最值;
的最值;
(Ⅱ)给出定理:如果函数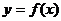 在区间[
在区间[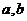 ]上连续,并且有
]上连续,并且有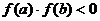 ,那么,函数
,那么,函数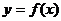 在区间
在区间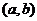 内有零点,即存在
内有零点,即存在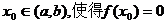 .
.
运用上述定理判断,当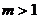 时,函数
时,函数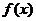 在区间
在区间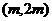 内是否存在零点.
内是否存在零点.
解:(I)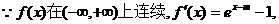
令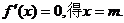 ……………………2分
……………………2分
|
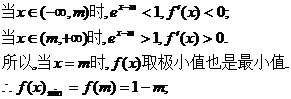
由①知f(x)无最大值. ……………………6分
(Ⅱ)函数f(x)在[m,2m]上连续.
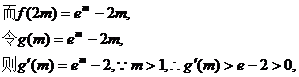
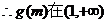 上递增. ……………………8分
上递增. ……………………8分
由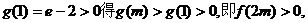 ……………………10分
……………………10分
又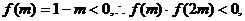
根据定理,可判断函数f(x)在区间(m,2m)上存在零点. ……………………12分
31.在平面直角坐标系中,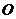 为坐标原点,已知两点
为坐标原点,已知两点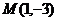 、
、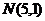 ,若点
,若点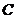 满足
满足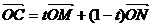 (
(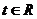 ),点
),点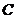 的轨迹与抛物线:
的轨迹与抛物线: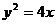 交于
交于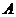 、
、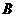 两点.
两点.
(Ⅰ)求证: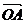 ⊥
⊥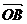 ;
;
(Ⅱ)在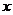 轴上是否存在一点
轴上是否存在一点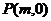 ,使得过点
,使得过点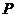 直线交抛物线于D、E两点,并以该弦DE为直径的圆都过原点。若存在,请求出
直线交抛物线于D、E两点,并以该弦DE为直径的圆都过原点。若存在,请求出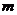 的值及圆心的轨迹方程;若不存在,请说明理由.
的值及圆心的轨迹方程;若不存在,请说明理由.
解:1)解:由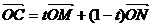 (
(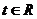 )知点
)知点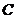 的轨迹是
的轨迹是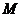 、
、 两点所在的直线,故 点
两点所在的直线,故 点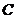 的轨迹方程是:
的轨迹方程是: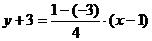 即
即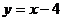 ………… ….2分
………… ….2分
由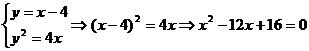
∴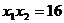
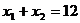
∴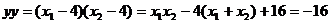
∴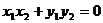 故
故 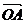 ⊥
⊥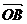 . ……………………………………6分
. ……………………………………6分
2)解:存在点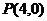 ,使得过点
,使得过点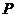 任作抛物线的一条弦,以该弦为直径的圆都过原点
任作抛物线的一条弦,以该弦为直径的圆都过原点
由题意知:弦所在的直线的斜率不为零 …………………………………7分
故 设弦所在的直线方程为: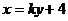 代入
代入 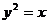 得
得 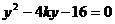
∴ 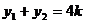
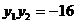
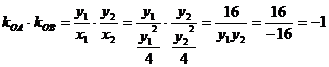
∴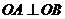 故以
故以 为直径的圆都过原点 …………………………..10分
为直径的圆都过原点 …………………………..10分
设弦 的中点为
的中点为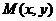 则
则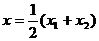
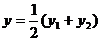
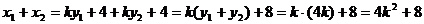
∴弦 的中点
的中点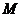 的轨迹方程为:
的轨迹方程为:
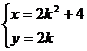 消去
消去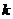 得
得 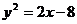 . ……………………14分
. ……………………14分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com