
题目列表(包括答案和解析)
18. (天津十二区县重点中学2010年高三联考一理)(本小题满分12分)
某射击游戏规定:每位选手最多射击3次;射击过程中若击中目标,方可进行下一次射击,否则停止射击;同时规定第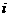
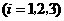 次射击时击中目标得
次射击时击中目标得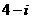 分,否则该次射击得
分,否则该次射击得 分。已知选手甲每次射击击中目标的概率为
分。已知选手甲每次射击击中目标的概率为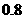 ,且其各次射击结果互不影响.
,且其各次射击结果互不影响.
(Ⅰ)求甲恰好射击两次的概率;
(Ⅱ)设该选手甲停止射击时的得分总和为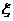 ,求随机变量
,求随机变量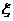 的分布列及数学期望.
的分布列及数学期望.
20. 解:(1)当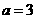 时,
时,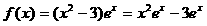 ,
,
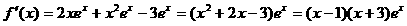 ,
,
令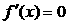 ,得
,得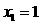 或
或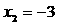 ,
,
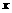 |
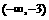 |
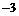 |
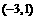 |
1 |
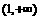 |
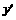 |
+ |
0 |
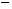 |
0 |
+ |
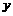 |
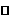 |
极大值 |
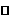 |
极小值 |
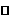 |
所以,函数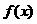 在
在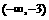 单调增,在
单调增,在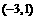 单调减,在
单调减,在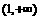 单调增.
单调增.
当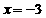 时,
时,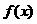 的极大值为
的极大值为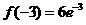 ;
;
当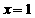 时,
时,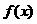 的极小值为
的极小值为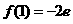 .
.
(2)由题设知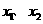 为
为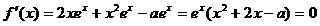 的两个根,
的两个根,
则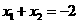 ,
,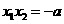 ,由
,由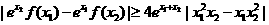 ,
,
得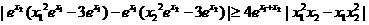 ,
,
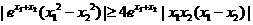 ,
,
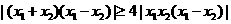 ,
,
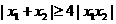 ,即
,即 ,所以,
,所以,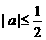 ,
,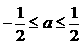 .
.
又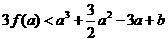 恒成立,
恒成立,
所以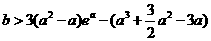 恒成立,
恒成立,
令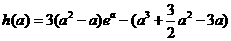 ,
,
则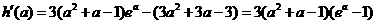 ,
,
当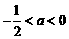 时,
时,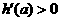
 ,
,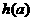 为增函数,
为增函数,
当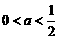 时,
时,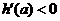
 ,
,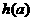 为减函数,
为减函数,
所以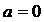 时,函数
时,函数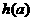 的极大值为
的极大值为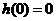 ,当
,当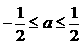 ,函数
,函数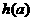 的最大值为0,所以
的最大值为0,所以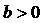 .
.
20.(天津市天津一中2010届高三第四次月考文科)设函数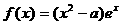 .
.
(1)若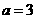 ,求
,求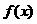 的单调区间和极值;
的单调区间和极值;
(2)若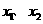 为
为
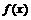 的两个不同的极值点,且
的两个不同的极值点,且
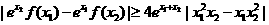 ,
,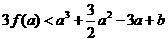 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
20、解:(1)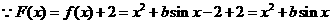 ,
,
依题意,对任意实数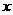 ,恒有
,恒有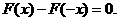
即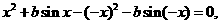
即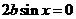
所以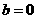 ,……………………(1分)
,……………………(1分)
所以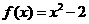 …………………… (2分)
…………………… (2分)
(2)
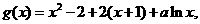
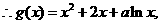
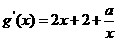 ……………………(3分)
……………………(3分)
 函数
函数 在(0,1)上单调递减,
在(0,1)上单调递减,
 在区间(0,1)
在区间(0,1)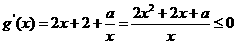 恒成立……………………(4分)
恒成立……………………(4分)

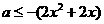 在(0,1)上恒成立
在(0,1)上恒成立
 而
而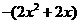 在(0,1)上单调递减
在(0,1)上单调递减
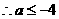 为所求。……………………(6分)
为所求。……………………(6分)
(3)
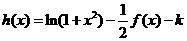 =
=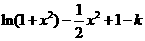 [来源:]
[来源:]
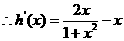
令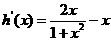 =0,解得
=0,解得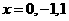
 当
当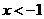 时,
时,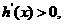 当
当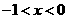 时,
时,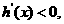
当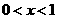 时,
时,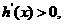 当
当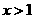 时,
时,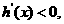
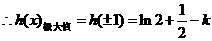 ……………………(7分)
……………………(7分)
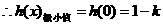 ……………………(8分)
……………………(8分)
所以①当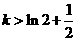 时,函数没有零点;……………………(9分)
时,函数没有零点;……………………(9分)
②当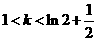 时,函数有四个零点;……………………(10分)
时,函数有四个零点;……………………(10分)
③当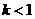 或
或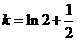 时,函数有两个零点;……………………(11分)
时,函数有两个零点;……………………(11分)
④当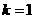 时,函数有三个零点;……………………(12分)
时,函数有三个零点;……………………(12分)
20.(天津市天津一中2010届高三第四次月考理科)已知函数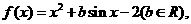
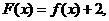 且对于任意实数
且对于任意实数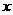 ,恒有
,恒有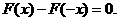
(1)求函数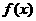 的解析式;
的解析式;
(2)已知函数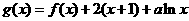 在区间
在区间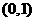 上单调递减,求实数
上单调递减,求实数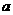 的取值范围;
的取值范围;
(3)函数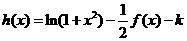 有几个零点?
有几个零点?
21.解:(1)①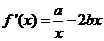
 函数
函数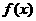 在
在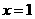 处与直线
处与直线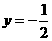 相切
相切
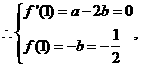
解得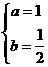 …………3分
…………3分
②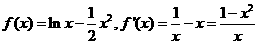
当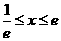 时,令
时,令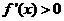 得
得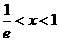 ;
;
令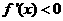 ,得
,得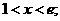
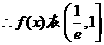 上单调递增,在[1,e]上单调递减,
上单调递增,在[1,e]上单调递减,
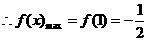 …………8分
…………8分
(2)当b=0时,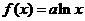
若不等式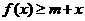 对所有的
对所有的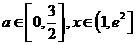 都成立,
都成立,
则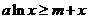 对所有的
对所有的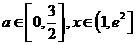 都成立,
都成立,
即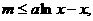 对所有的
对所有的 都成立,
都成立,
令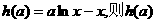 为一次函数,
为一次函数,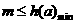
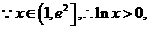
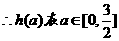 上单调递增
上单调递增
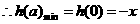 ,
,
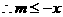 对所有的
对所有的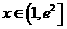 都成立
都成立
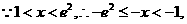
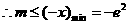 …………14分
…………14分
(注:也可令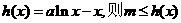 所有的
所有的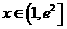 都成立,分类讨论得
都成立,分类讨论得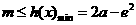 对所有的
对所有的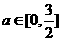 都成立,
都成立,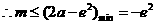 ,请根据过程酌情给分)
,请根据过程酌情给分)
21.(天津市六校2010届高三第三次联考文科)(本小题满分14分)
设函数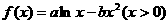
(1)若函数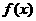 在x=1处与直线
在x=1处与直线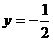 相切
相切
①求实数a,b的值;
②求函数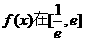 上的最大值.
上的最大值.
(2)当b=0时,若不等式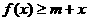 对所有的
对所有的 都成立,求实数m的取值范围.
都成立,求实数m的取值范围.
22.解:(I)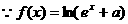 是奇函数,
是奇函数,
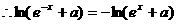 …………1分
…………1分
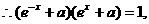
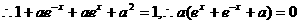 故a=0 …………3分
故a=0 …………3分
(II)由(I)知: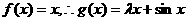 ,
,
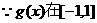 上单调递减,
上单调递减,
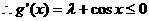
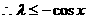 在[-1,1]上恒成立,
在[-1,1]上恒成立,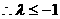 …………5分
…………5分
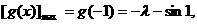
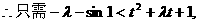
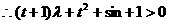 (其中
(其中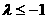 ),恒成立,
),恒成立,
令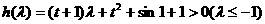 ,
,
则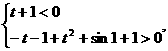
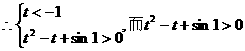 恒成立,
恒成立,
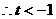 …………8分
…………8分
(III)由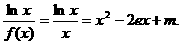 …………9分
…………9分
令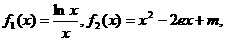
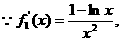
当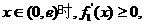
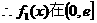 上为增函数;
上为增函数;
当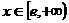 时,
时,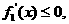
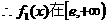 为减函数;
为减函数;
当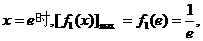
而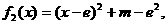 …………11分
…………11分
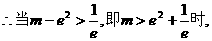 方程无解;
方程无解;
当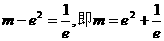 时,方程有一个根;
时,方程有一个根;
当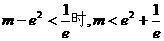 时,方程有两个根. …………14分
时,方程有两个根. …………14分
22.(天津市六校2010届高三第三次联考理科)(本小题14分)
已知函数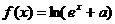 (a为常数)是R上的奇函数,函数
(a为常数)是R上的奇函数,函数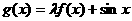
是区间[-1,1]上的减函数.
(I)求a的值;
(II)若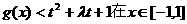 上恒成立,求t的取值范围;
上恒成立,求t的取值范围;
(III)讨论关于x的方程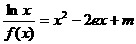 的根的个数.
的根的个数.
19.(天津市武清区2009-2010学年高三下学期第一次模拟文)(本小题满分12分)
已知三次函数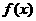 =
=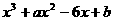 ,
,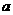 、
、 为实数,
为实数, ,曲线
,曲线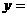
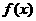 在点(1,
在点(1,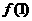 )处切线的斜率为-6。
)处切线的斜率为-6。
(1)求函数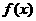 的解析式;
的解析式;
(2)若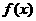
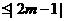 对任意的
对任意的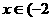 ,2)恒成立,求实数
,2)恒成立,求实数 的取值范围。
的取值范围。
解:(1)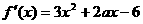 ……………1分
……………1分
由导数的几何意义,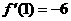 ∴
∴ 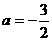 ……………2分
……………2分
∵  ∴
∴ 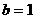 …………………3分
…………………3分
∴ 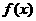 =
=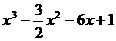 ………………4分
………………4分
(2)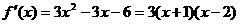
令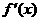 =0得
=0得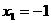 ,
,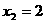 …………………5分
…………………5分
当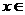 (-2,-1)时,
(-2,-1)时,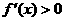 ,
,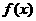 递增;
递增;
当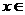 (-1,2)时,
(-1,2)时,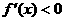 ,
,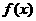 递减。……………7分
递减。……………7分
∴ 在区间(-2,2)内,函数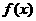 的最大值为
的最大值为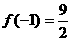 ………………8分
………………8分
∵ 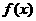
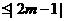 对任意的
对任意的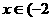 ,2)恒成立
,2)恒成立
∴
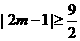 ………………10分
………………10分
∴ 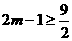 或
或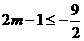
∴ 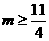 或
或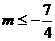 ………………………12分
………………………12分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com