
题目列表(包括答案和解析)
88. 已知:直线a∥平面 .求证:经过a和平面
.求证:经过a和平面 平行的平面有且仅有一个.
平行的平面有且仅有一个.
证:过a作平面与 交于
交于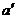 ,在
,在 内作直线
内作直线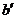 与
与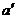 相交,在a上任取一点P,在
相交,在a上任取一点P,在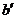 和P确定的平面内,过P作b∥
和P确定的平面内,过P作b∥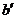 .b在
.b在 外,
外,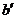 在
在 内,
内,
∴ b∥
而a∥
∴ a,b确定的平面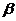 过a且平行于
过a且平行于 .
.
∵ 过a,b的平面只有一个,
∴ 过a平行于平面 的平面也只有一个
的平面也只有一个
87. 已知正三棱柱ABC-A1B1C1,底面边长为8,对角线B1C=10,D为AC的中点.
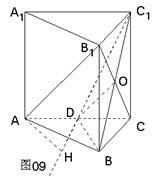 (1) 求证AB1∥平面C1BD;
(1) 求证AB1∥平面C1BD;
(2) 求直线AB1到平面C1BD的距离.
证明:(1) 设B1C∩BC1=O.
连DO,则O是B1C的中点.
在△ACB1中,D是AC中点,O是B1C中点.
∴ DO∥AB1,
又DO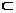 平面C1BD,AB1
平面C1BD,AB1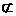 平面C1BD,
平面C1BD,
∴ AB1∥平面C1BD.
解:(2) 由于三棱柱ABC-A1B1C1是正三棱柱,D是AC中点,
∴ BD⊥AC,且BD⊥CC1,
∴ BD⊥平面AC1,
平面C1BD⊥平面AC1,C1D是交线.
在平面AC1内作AH⊥C1D,垂足是H,
∴ AH⊥平面C1BD,
又AB1∥平面C1BD,故AH的长是直线AB1到平面C1BD的距离.
由BC=8,B1C=10,得CC1=6,
在Rt△C1DC中,DC=4,CC1=6,
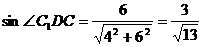
在Rt△DAH中,∠ADH=∠C1DC
∴ 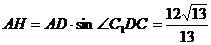 .
.
即AB1到平面C1BD的距离是 .
.
评述:证明线面平行的关键是在平面内找出与已知直线平行的直线,如本题的DO.本题的第(2)问,实质上进行了“平移变换”,利用AB1∥平面C1BD,把求直线到平面的距离变换为求点A到平面的距离.
86. 已知:正方体ABCD-A1B1C1D1棱长为a.
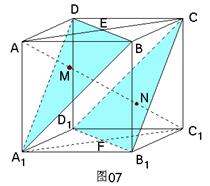 (1) 求证:平面A1BD∥平面B1D1C;
(1) 求证:平面A1BD∥平面B1D1C;
(2) 求平面A1BD和平面B1D1C的距离.
证明:(1) 在正方体ABCD-A1B1C1D1中,
∵ BB1平行且等于DD1,
∴ 四边形BB1D1D是平行四边形,
∴ BD∥B1D1,
∴ BD∥平面B1D1C.
同理 A1B∥平面B1D1C,
又A1B∩BD=B,
∴ 平面A1BD∥平面B1D1C
解:(2) 连AC1交平面A1BD于M,交平面B1D1C于N.
 AC是AC1在平面AC上的射影,又AC⊥BD,
AC是AC1在平面AC上的射影,又AC⊥BD,
∴ AC1⊥BD,
同理可证,AC1⊥A1B,
∴ AC1⊥平面A1BD,即MN⊥平面A1BD,
同理可证MN⊥平面B1D1C.
∴ MN的长是平面A1BD到平面B1D1C的距离,
设AC、BD交于E,则平面A1BD与平面A1C交于直线A1E.
∵ M∈平面A1BD,M∈AC1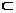 平面A1C,
平面A1C,
∴ M∈A1E.
同理N∈CF.
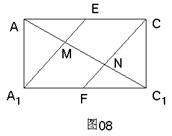
在矩形AA1C1C中,见图9-21(2),由平面几何知识得
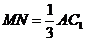 ,
,
∴ 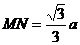 .
.
评述:当空间图形较为复杂时,可以分解图形,把其中的平面图形折出分析,利于清楚地观察出平面上各种线面的位置关系.证明面面平行,主要是在其中一个平面内找出两条与另一个平面平行的相交直线,或者使用反证法.
85.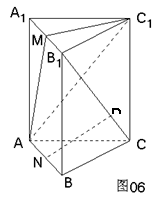 已知直三棱柱ABC-A1B1C1中,AC=BC,M、N分别是A1B1,AB的中点,P点在线段B1C上,则NP与平面AMC1的位置关系是 ( )
已知直三棱柱ABC-A1B1C1中,AC=BC,M、N分别是A1B1,AB的中点,P点在线段B1C上,则NP与平面AMC1的位置关系是 ( )
(A) 垂直
(B) 平行
(C) 相交但不垂直
(D) 要依P点的位置而定
解析:由题设知B1M∥AN且B1M=AN,
四边形ANB1M是平行四边形,
故B1N∥AM,B1N∥AMC1平面.
又C1M∥CN,得CN∥平面AMC1,则平面B1NC∥AMC1,NP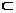 平面B1NC,
平面B1NC,
∴ NP∥平面AMC1.
答案选B.
84. 已知a、b、c是三条不重合的直线,α、β、r是三个不重合的平面,下面六个命题:
①a∥c,b∥c a∥b;
a∥b;
②a∥r,b∥r a∥b;
a∥b;
③α∥c,β∥c α∥β;
α∥β;
④α∥r,β∥r α∥β;
α∥β;
⑤a∥c,α∥c a∥α;
a∥α;
⑥a∥r,α∥r a∥α.
a∥α.
其中正确的命题是 ( )
(A) ①④ (B) ①④⑤
(C) ①②③ (D) ①⑤⑥
解析:由公理4“平行于同一条直线的两条直线互相平行”可知命题①正确;若两条不重合的直线同平行于一个平面,它们可能平行,也可能异面还可能相交,因此命题②错误;平行于同一条直线的两个不重合的平面可能平行,也可能相交,命题③错误;平行于同一平面的两个不重合的平面一定平行,命题④正确;若一条直线和一个平面分别平行于同一条直线或同一个平面,那么这条直线与这个平面或平行,或直线在该平面内,因此命题⑤、⑥都是错的,答案选A.
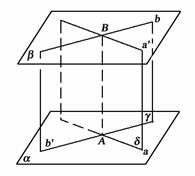
83. 已知:a、b是异面直线,a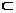 平面,b
平面,b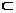 平面,a∥,b∥.
平面,a∥,b∥.
 求证:∥.
求证:∥.
证法1:在a上任取点P,
 显然P∈b.
显然P∈b.
 于是b和点P确定平面.
于是b和点P确定平面.
且与有公共点P
∴ ∩=b′
且b′和a交于P,
∵ b∥,
∴ b∥b′
∴ b′∥
而a∥
这样内相交直线a和b′都平行于
∴ ∥.
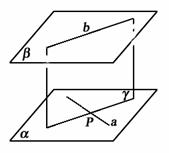
 证法2:设AB是a、b的公垂线段,
证法2:设AB是a、b的公垂线段,
过AB和b作平面,
∩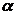 =b′,
=b′,
过AB和a作平面,
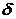 ∩=a′.
∩=a′.
a∥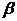
 a∥a′
a∥a′
b∥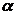
 b∥b′
b∥b′
∴AB⊥a AB⊥a′,AB⊥b
AB⊥a′,AB⊥b AB⊥b′
AB⊥b′
于是AB⊥且AB⊥,∴ ∥.
82. 两个平面同时垂直于一条直线,则两个平面平行.
已知:、是两个平面,直线l⊥,l⊥,垂足分别为A、B.
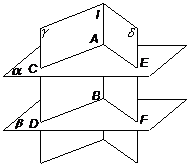 求证:∥思路1:根据判定定理证.
求证:∥思路1:根据判定定理证.
证法1:过l作平面,
∩=AC,∩=BD,
过l作平面,
∩=AE,∩=BF,
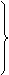 l⊥
l⊥ l⊥AC
l⊥AC
l⊥ l⊥BD
l⊥BD  AC∥BD
AC∥BD AC∥,
AC∥,
l、AC、BD共面
同理AE∥,AC∩AE≠,AC,AE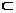 ,故∥.
,故∥.
思路2:根据面面平行的定义,用反证法.
证法2:设、有公共点P
则l与P确定平面,
且∩=AP,∩=BP.
l⊥ l⊥AP
l⊥AP
l⊥ l⊥BP
l⊥BP
l、AP、BP共面,于是在同一平面内过一点有两条直线AP、BP都与l垂直,这是不可能的.
故、不能有公共点,∴ ∥.
81. 有三个几何事实(a,b表示直线, 表示平面),① a∥b,②
a∥
表示平面),① a∥b,②
a∥ ,③
b∥
,③
b∥ .其中,a,b在面
.其中,a,b在面 外.
外.
用其中两个事实作为条件,另一个事实作为结论,可以构造几个命题?请用文字语言叙述这些命题,并判断真伪.正确的给出证明,错误的举出反例.
解析:Ⅰ: a∥b
a∥
 b∥
b∥
b在 外
外
Ⅱ:a∥b
b∥
 a∥
a∥
a在 外
外
Ⅰ、Ⅱ是同一个命题:两条平行直线都在一个平面外,若其中一条与平面平行,则另一条也与该平面平行.
证明:过a作平面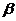 与
与 交于
交于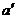
∵ a∥
∵ a∥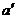
而a∥b
∴ b∥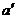 且b在
且b在 外,
外,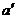 在
在 内
内
∴ b∥ .
.
 Ⅲ:a∥
Ⅲ:a∥
 a∥b
a∥b
b∥
命题:平行于同一个平面的两条直线平行,
这是错的,如右图
20. 已知f(x)是定义域为(0,+∞)的函数,当x∈(0,1)时f(x)<0.现针对任意正实数x、y,给出下列四个等式:
① f(xy)=f(x) f(y) ;② f(xy)=f(x)+f(y) ;③ f(x+y)=f(x)+f(y) ; ④ f(x+y)=f(x) f(y) .
请选择其中的一个等式作为条件,使得f(x)在(0,+∞)上为增函数;并证明你的结论.
解:你所选择的等式代号是 .
19.已知二次函数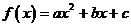 .
.
(1)若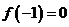 ,试判断函数
,试判断函数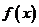 零点个数;
零点个数;
(2)若对任意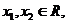 且
且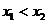 ,
,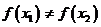 ,试证明存在
,试证明存在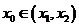 ,
,
使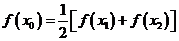 成立.
成立.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com