
题目列表(包括答案和解析)
例2
求过定点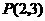 ,且在两坐标轴上的截距相等的直线方程.
,且在两坐标轴上的截距相等的直线方程.
误:设直线在两坐标轴上的截距为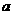 ,故所求的直线方程为
,故所求的直线方程为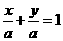 ,即
,即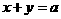 .
.
将点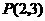 代入,得
代入,得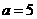 .
.
故所求直线方程为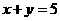 .
.
析:本题由于忽视了“零截距”而导致错误.事实上,当两截距均为零时也满足条件,所以应增加截距均为零的情况.当直线在两坐标轴上的截距为零时,设所求的直线方程为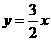 ,即
,即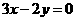 .所以,所求直线方程为
.所以,所求直线方程为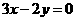 或
或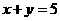 .
.
事实上,当题中出现“截距相等”、“截距的绝对值相等”、“截距互为相反数”,“在一坐标轴上的截距是另一坐标轴上的截距的 倍(
倍(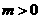 )”等条件时,若采用截距式求直线方程,都要考虑“零截距”的情况.当然本题可设直线方程为
)”等条件时,若采用截距式求直线方程,都要考虑“零截距”的情况.当然本题可设直线方程为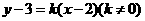 ,分别令
,分别令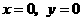 解得直线在两坐标轴上的截距,由其相等解得
解得直线在两坐标轴上的截距,由其相等解得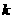 ,从而得到直线方程.
,从而得到直线方程.
例1
求过定点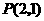 且与坐标轴围成的三角形的面积为4的直线方程.
且与坐标轴围成的三角形的面积为4的直线方程.
误:设所求的直线方程为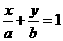 .
.
 直线过点
直线过点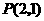 ,
,
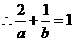 ,即
,即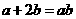 , ①
, ①
又由已知,可得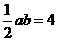 ,即
,即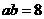 , ②
, ②
由①,②可得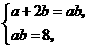 解得
解得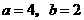 .
.
故所求直线方程为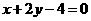 .
.
析:本题由于对截距的概念不清,混淆了“距离”与“截距”的概念,误将直线在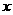 轴和
轴和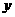 轴上的截距作为距离使用而导致错误.事实上,直线与两坐标轴围成的三角形的面积为
轴上的截距作为距离使用而导致错误.事实上,直线与两坐标轴围成的三角形的面积为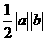 而不是
而不是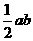 .故应有
.故应有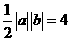 ③,由①,③易得所求直线方程为
③,由①,③易得所求直线方程为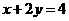 ,或
,或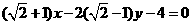 ,或
,或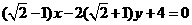 .
.
1.2万件、1.3万件、1.37万件.由于产品质量好服装款式新颖,因此前几个月的产品销售情况良好.为了使推销员在推销产品时,接收订单不至于过多或过少,需要估测以后几个月的产量,假如你是厂长,将采用什么方法?
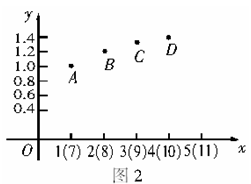
分析:首先建立直角坐标系,画出散点图(如图2所示),其次根据散点图,我们可以设想函数模型.可能为一次函数型: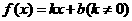 ;
;
二次函数型: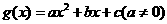 ;
;
幂函数型: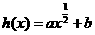 ;指数函数型:
;指数函数型: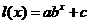 ,
,
最后用待定系数法求出各解析式,并验证,选出合适的函数.
解:设月产量为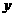 万件,月份数为
万件,月份数为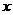 ,建立直角坐标系,
,建立直角坐标系,
可得 .
.
(1)
对于直线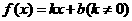 ,将
,将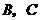 两点的坐标代入,有
两点的坐标代入,有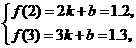 解得
解得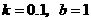 ,故
,故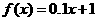 .
.
将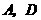 两点的坐标代入,得
两点的坐标代入,得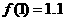 ,与实际误差为0.1;
,与实际误差为0.1;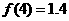 ,与实际误差为0.03.
,与实际误差为0.03.
(2)
对于二次函数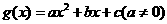 ,将
,将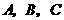 三点的坐标代入,
三点的坐标代入,
有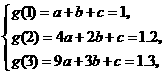 解得
解得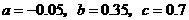 ,
,
故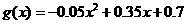 .
.
将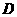 点的坐标代入,得
点的坐标代入,得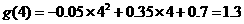 ,与实际误差为0.07.
,与实际误差为0.07.
(3)
对于幂函数型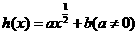 ,将
,将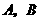 两点的坐标代入,
两点的坐标代入,
得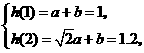
解得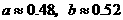 ,
,
故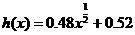 .
.
将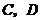 两点的坐标代入,得
两点的坐标代入,得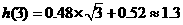 ,与实际误差为0.05;
,与实际误差为0.05;
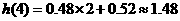 ,与实际误差为0.11.
,与实际误差为0.11.
(4)
对于指数函数型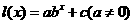 ,将
,将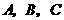 三点的坐标代入,
三点的坐标代入,
有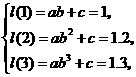
解得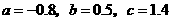 .
.
故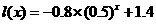 .
.
将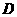 点的坐标代入,得
点的坐标代入,得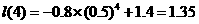 ,与实际误差为0.02.
,与实际误差为0.02.
比较上述4个模拟函数的优劣,既要考虑到与实际误差最小,又要考虑到生产的实际问题,比如增产的趋势和可能性.所以可以认为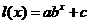 最佳,一是误码差最小,二是由于新建厂,开始随着技术、管理效益逐渐提高,一段时间内产量明显上升,但到一定时间后,设备不更新,那么产量必然要趋于稳定,而
最佳,一是误码差最小,二是由于新建厂,开始随着技术、管理效益逐渐提高,一段时间内产量明显上升,但到一定时间后,设备不更新,那么产量必然要趋于稳定,而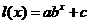 恰好反映了这种趋势,因此选用
恰好反映了这种趋势,因此选用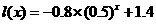 比较接近客观实际.
比较接近客观实际.
例2 三个平面可以将空间分成几个部分?
解析:(1)三个平面平行,画成如图3,得知分成4个部分;
(2)两个平面平行时,画成如图4,得知分成6个部分;
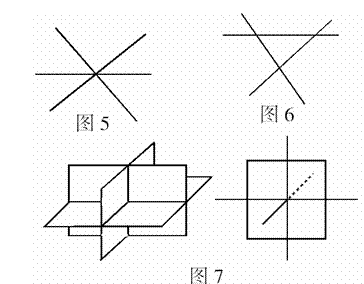
(3)三个平面交于同一条直线,画成如图5,得知分成6人部
分;
(4)三个平面交于三条直线,画成如图6和图7,得知分成7
个或8个部分.
例1
画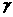 平面和两个平行平面
平面和两个平行平面 相交的
相交的
立体图形,如图1.
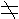 画图步骤:首先画出图1中的“
画图步骤:首先画出图1中的“ ”图,再从两个交点处出发,画出两条平行等长线段,画出两条平行等长线段,继而画出6条同方向的平行等长线段,连结成三个平面,最后把被前面的平面遮住的线段改成虚线,过程如图2所示.
”图,再从两个交点处出发,画出两条平行等长线段,画出两条平行等长线段,继而画出6条同方向的平行等长线段,连结成三个平面,最后把被前面的平面遮住的线段改成虚线,过程如图2所示.

例3 方程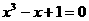 在区间
在区间 (
(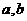 是整数,且
是整数,且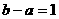 )上有一个根,则
)上有一个根,则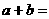 .
.
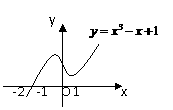 解 令
解 令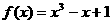 ,作出函数图象.
,作出函数图象.
∵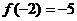 ,
,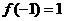 ,
,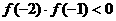 ,
,
∴方程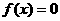 在区间
在区间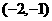 内有一根.
内有一根.
∵函数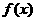 在
在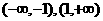 上都是增函数;又当
上都是增函数;又当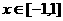 时,
时,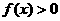 恒成立.
恒成立.
故方程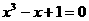 在
在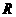 上只有一解,又
上只有一解,又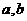 是整数,且
是整数,且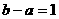 ,∴
,∴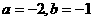 ,故
,故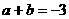 .
.
点评:一般解决此类逆向问题的三步曲是:①先通过观察函数图象再估算出根所在的区间;②根据方程根的存在性定理证明根是存在的;③最后根据函数的性质证明根是唯一的.
例2 若方程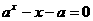 有两个解,则
有两个解,则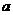 的取值范围是( )
的取值范围是( )
(A)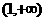 (B)
(B)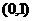 (C)
(C)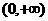 (D)
(D)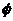
解 原方程移项得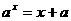 ,令
,令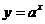 ,
,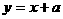 .
.
 当
当 时,在同一直角坐标系内作出
时,在同一直角坐标系内作出
函数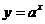 ,
,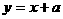 的图象,由图观察得
的图象,由图观察得
原方程有两个解,从而排除(B)(D);
又当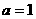 时,原方程为
时,原方程为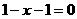 ,解
,解
得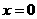 ,只有一解,从而排除(C),故选(A).
,只有一解,从而排除(C),故选(A).
点评:若令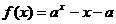 ,则很难作出该函数的图象. 一般解决此类逆向问题的三步曲是:①先移项使之分解为两个简单函数;②在同一坐标系内作出这两个函数图象;③数它们交点的个数即为方程根的个数.
,则很难作出该函数的图象. 一般解决此类逆向问题的三步曲是:①先移项使之分解为两个简单函数;②在同一坐标系内作出这两个函数图象;③数它们交点的个数即为方程根的个数.
例1 方程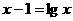 必有一个根的区间是( )
必有一个根的区间是( )
(A)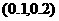 (B)
(B)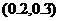 (C)
(C)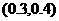 (D)
(D)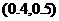
解 原方程移项得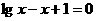 ,令
,令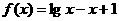 ,∵
,∵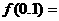
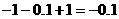 ,
,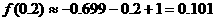 ,即
,即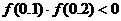 ,∴方程
,∴方程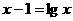 必有一个根在区间
必有一个根在区间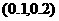 内,故选(A).
内,故选(A).
点评:利用方程根的存在性定理求解三步曲是:①先移项使方程右边为零,再令方程左边为函数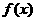 ;②求区间
;②求区间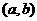 两端点的函数值
两端点的函数值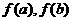 ;③若函数在该区间上连续且
;③若函数在该区间上连续且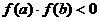 ,则方程在该区间内必有根.
,则方程在该区间内必有根.
3. 多转化――生熟变通
条件给出的内容,有时具有很强的隐蔽性,我们时常会感到很生疏.为揭示其隐蔽性,需对条件进行转化,经过几次转化后生疏的变为熟悉的,解法自然也就产生了.
例3
对于函数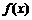 ,若
,若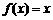 ,则称
,则称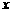 为函数
为函数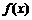 的“不动点”;若
的“不动点”;若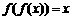 ,称
,称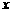 为函数
为函数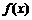 的“稳定点”.函数
的“稳定点”.函数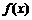 的“不动点”和“稳定点”的集合分别记为
的“不动点”和“稳定点”的集合分别记为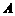 和
和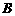 .
.
(1) 求证: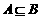 ;
;
(2) 若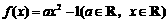 ,且
,且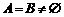 ,求实数
,求实数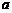 的取值范围.
的取值范围.
解析:本题中的条件有三个:①若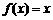 ,则称
,则称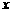 为函数
为函数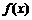 的“不动点”;②若
的“不动点”;②若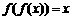 ,则称
,则称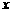 为函数
为函数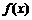 的“稳定点”;③“不动点”和“稳定点”的集合分别记为
的“稳定点”;③“不动点”和“稳定点”的集合分别记为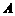 和
和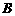 .把条件转化一下,就是
.把条件转化一下,就是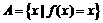 ,
,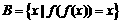 ,因此
,因此
(1) 若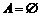 ,则
,则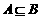 成立;
成立;
若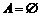 ,设
,设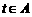 ,则
,则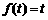 ,显然
,显然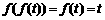 ,即
,即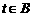 ,那么
,那么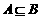 ;
;
(2) 由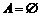 ,得方程
,得方程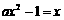 有实根,
有实根,
故有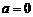 ,或
,或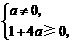 解得
解得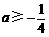 .
.
由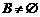 ,得方程
,得方程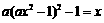 ,即
,即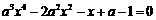 有实根,又由
有实根,又由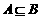 可知,方程左边必含有
可知,方程左边必含有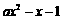 ,于是
,于是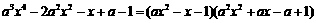 , 由于
, 由于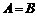 ,因此方程
,因此方程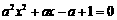 要么没有实根,要么实根是方程
要么没有实根,要么实根是方程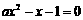 的根.
的根.
若方程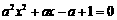 没有实根,则
没有实根,则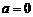 ,或
,或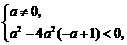 得
得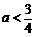 ;
;
若方程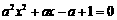 有实根
有实根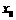 ,
,
则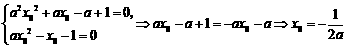 ,
,
那么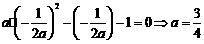 .
.
故实数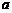 的取值范围为
的取值范围为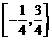 .
.
点评:“不动点”、“稳定点”及这些点构成的集合,这么多的新东西,其实是变相的告诉你两个集合.当你完成对条件的转化后,求解就变得简单多了.
2. 抓特征――诱发联想
特征是题目的“个性”,是“此类题”区别于“彼类题”的关键.抓住特征,可以诱发
联想.通过对往日解题经验的回顾,达到求解的目的.
例2
设函数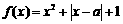 ,求
,求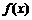 最小值
最小值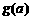 的最小值.
的最小值.
解析:本题的特征是:①含绝对值;②最小值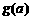 的最最小值.抓住这两个特征我们会想到首先去绝对值符号,由于去绝对值符号时要分
的最最小值.抓住这两个特征我们会想到首先去绝对值符号,由于去绝对值符号时要分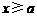 与
与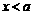 两种情况,所以
两种情况,所以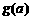 应该是分段函数.于是:
应该是分段函数.于是:
(1) 若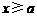 ,则
,则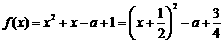 .
.
当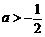 时,
时,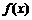 在
在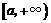 上是增函数,那么
上是增函数,那么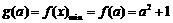 ;
;
当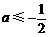 时,
时,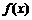 在
在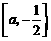 上是减函数,在
上是减函数,在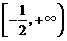 上是增函数,
上是增函数,
那么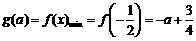 .
.
(2)若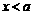 ,则
,则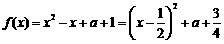 .
.
当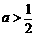 时,
时,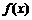 在
在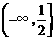 上是减函数,在
上是减函数,在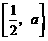 上是增函数,
上是增函数,
那么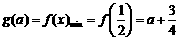 .
.
当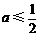 时,
时,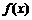 在
在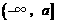 上是减函数,那么
上是减函数,那么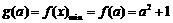 .
.
由(1),(2)得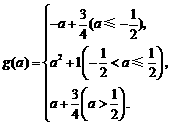
结合图形可知,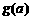 的最小值为1.
的最小值为1.
点评:本题表面上看好象较"温柔",其实"柔中有刚".当我们抓住特征去掉绝对值以后,求解的关键变成了对二次函数在部分区间上的单调性的判断.由于含有参变量,因此必须小心谨慎才行.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com