涉及到与函数有关的问题内容非常广泛，但限于我们目前所学的知识有限，只能举一些简单方面的应用，以后随着新知识的增加，可再深入到一些其它方面的应用.

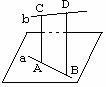
例1、如图，已知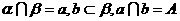，且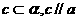，求证：b，c为异面

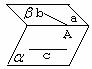直线。

证明：(1)因为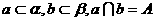，所以b与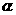只有一个公共点，而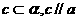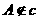，，所以c与b无公共点。

(2)因为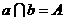，b上只有一个点在平面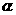内，又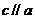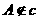，，所以c，b不在同一平面内。

结合(1)、(2)知，b，c是异面直线。

点评：“异面直线”与“分别在某两个平面内的两条直线”含义不同，前者是指不可能找到一个平面同时包含这两条直线，后者的两条直线只是位于两个平面内，他们有可能同时在第三个平面内，利用定义重在证明无公共点又不在同一平面内。

例2、如图，已知直线a、b是异面直线，A、B是a上相异两点，C、D是b上相异两点，求证：AC、BD是异面直线。

分析：利用反证法

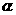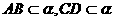证明：假设直线AC、BD不是异面直线，则它们必共面，所以A、B、C、D在同一平面内，所以即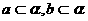，这与a、b是异面直线矛盾，所以AC、BD是异面直线。

点评：反证法是证明否定命题的基本方法，在立体几何中，下面三类问题常用反证法：

(1)直接利用公理、定义证题，即在尚未建立有关定理作为依据的情况下证题；

(2)证明某些唯一性结论的命题；

(3)所证结论是一种否定性的命题。

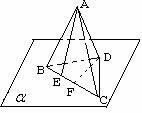
例3、如图，空间四边形ABCD中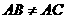，，AE是▲ABC的边BC上的高，DF为▲DBC的边BC上的中线，求证：AE和DF是异面直线。

证明：由题设条件可知点E、F不重合，设▲BCD所在平面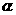为，因为

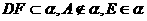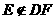，，所以AE和DF是异面直线。

点评：利用判定定理时必须阐述出定理满足的条件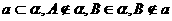：，然后可以推出直线a与AB是异面直线。

3、反证法：反证法是立体几何中证明的一种重要方法，反证法证题的步骤是：(1)提

出与结论相反的假设；(2)由此假设推出与已知条件或某一公理、定理或某一已被证明是正确的命题相矛盾的结果；(3)推翻假设，从而肯定与假设相反的结论，即命题的结论。

2、过平面外一点与平面内一点的直线，和平面内不过该点的直线是异面直线。

1、由定义判定两直线不可能在同一平面内；

异面直线定义中“不同在任何一个平面内”是指这两条直线“不能确定一个平面”，其

中的“任何”是异面直线不可缺少的前提条件。

不能把“不同在任何一个平面内”误解为“不同在某一个平面内”，如图1，直线

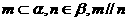，不能由m，n不同在平面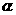上就误认为m，n异面，实际上，因可知，m与n共面，它们不是异面直线。也不能误解为“分别在某两个平面内的两条直线”，前者是说不可能找到一个同时包含这两条直线的平面，而后者的直线只是画在某两个平面内，并不能确定这两条直线异面，它们可以是平行直线，也可以是相交直线，如图2所示。

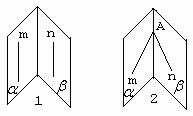
不同在任何一个平面内的两条直线叫做异面直线。

分割法也是体积计算中的一种常用方法，在求一些不规则的几何体的体积以及求两个几何体的体积之比时经常要用到分割法．

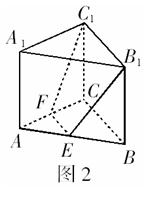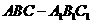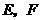例2　如图2，在三棱柱中，分别为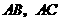的中点，平面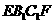将三棱柱分成两部分，求这两部分的体积之比．

分析：截面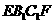将三棱柱分成两部分，一部分是三棱台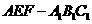；另一部分是一个不规则几何体，其体积可以利用棱柱的体积减去棱台的体积求得．

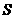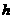解：设棱柱的底面积为，高为，其体积．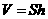

则三角形的面积为．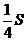

由于，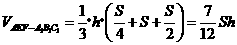

则剩余不规则几何体的体积为，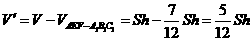

所以两部分的体积之比为．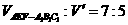

评注：在求一个几何体被分成的两部分体积之比时，若有一部分为不规则几何体，则可用整个几何体的体积减去规则几何体的体积求出其体积，再进行计算．