
题目列表(包括答案和解析)
4、已知向量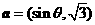 ,
,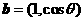 ,
,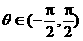 ,则
,则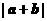 的最大值为 .
的最大值为 .
3、已知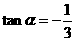 ,
,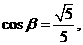
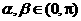 ,则
,则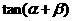 的值等于 .
的值等于 .
2、设动直线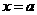 与函数
与函数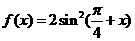 和
和
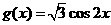 的图象分别交于
的图象分别交于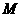 、
、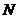 两点,则
两点,则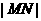 的最大值为( )
的最大值为( )
A.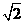 B.
B.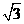 C.2
D.3高考
C.2
D.3高考
1、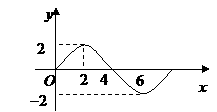 函数
函数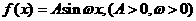 的部分图象如图
的部分图象如图
所示,则函数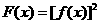 是 ( )
是 ( )
A.周期为4的偶函数 B.周期为4的奇函数
C.周期为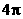 的偶函数 D.周期为
的偶函数 D.周期为 的奇函数
的奇函数
3.2简单的三角恒等变换
抽象函数的性质所对应的一些具体特殊函数模型:
①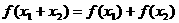
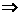 正比例函数
正比例函数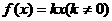
②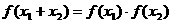 ;
;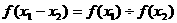
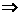 ;
;
③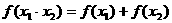 ;
;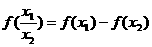
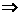 ;
;
④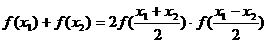
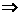 ;
;
定义域: ;值域: ; 奇偶性: ; 单调性: 是增函数; 是减函数。
(1)一元一次函数: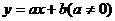 ,当
,当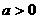 时,是增函数;当
时,是增函数;当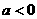 时,是减函数;
时,是减函数;
(2)一元二次函数:
一般式: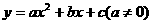 ;对称轴方程是
;顶点为
;
;对称轴方程是
;顶点为
;
两点式: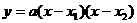 ;对称轴方程是
;与
;对称轴方程是
;与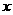 轴的交点为
;
轴的交点为
;
顶点式: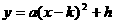 ;对称轴方程是
;顶点为
;
;对称轴方程是
;顶点为
;
①一元二次函数的单调性:
当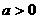 时:
为增函数; 为减函数;当
时:
为增函数; 为减函数;当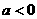 时:
为增函数; 为减函数;
时:
为增函数; 为减函数;
②二次函数求最值问题:首先要采用配方法,化为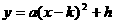 的形式,
的形式,
Ⅰ、若顶点的横坐标在给定的区间上,则
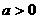 时:在顶点处取得最小值,最大值在距离对称轴较远的端点处取得;
时:在顶点处取得最小值,最大值在距离对称轴较远的端点处取得;
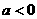 时:在顶点处取得最大值,最小值在距离对称轴较远的端点处取得;
时:在顶点处取得最大值,最小值在距离对称轴较远的端点处取得;
Ⅱ、若顶点的横坐标不在给定的区间上,则
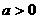 时:最小值在距离对称轴较近的端点处取得,最大值在距离对称轴较远的端点处取得;
时:最小值在距离对称轴较近的端点处取得,最大值在距离对称轴较远的端点处取得;
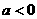 时:最大值在距离对称轴较近的端点处取得,最小值在距离对称轴较远的端点处取得;
时:最大值在距离对称轴较近的端点处取得,最小值在距离对称轴较远的端点处取得;
有三个类型题型:
(1)顶点固定,区间也固定。如: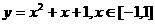
(2)顶点含参数(即顶点变动),区间固定,这时要讨论顶点横坐标何时在区间之内,何时在区间之外。
(3)顶点固定,区间变动,这时要讨论区间中的参数.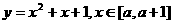
③二次方程实数根的分布问题: 设实系数一元二次方程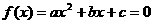 的两根为
的两根为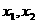 ;则:
;则:
|
根的情况 |
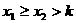 |
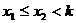 |
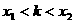 |
|
等价命题 |
在区间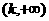 上有两根 上有两根 |
在区间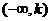 上有两根 上有两根 |
在区间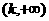 或 或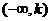 上有一根 上有一根 |
|
充要条件 |
|
|
|
注意:若在闭区间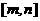 讨论方程
讨论方程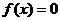 有实数解的情况,可先利用在开区间
有实数解的情况,可先利用在开区间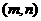 上实根分布的情况,得出结果,在令
上实根分布的情况,得出结果,在令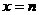 和
和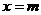 检查端点的情况。
检查端点的情况。
(3)反比例函数: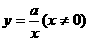
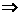
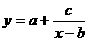
(4)指数函数: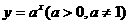
指数运算法则: ; ; 。
指数函数:y=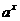 (a>o,a≠1),图象恒过点(0,1),单调性与a的值有关,在解题中,往往要对a分a>1和0<a<1两种情况进行讨论,要能够画出函数图象的简图。
(a>o,a≠1),图象恒过点(0,1),单调性与a的值有关,在解题中,往往要对a分a>1和0<a<1两种情况进行讨论,要能够画出函数图象的简图。
(5)对数函数: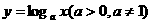
指数运算法则: ; ; ;
对数函数:y=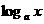 (a>o,a≠1) 图象恒过点(1,0),单调性与a的值有关,在解题中,往往要对a分a>1和0<a<1两种情况进行讨论,要能够画出函数图象的简图。
(a>o,a≠1) 图象恒过点(1,0),单调性与a的值有关,在解题中,往往要对a分a>1和0<a<1两种情况进行讨论,要能够画出函数图象的简图。
注意:(1)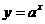 与
与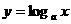 的图象关系是
;
的图象关系是
;
(2)比较两个指数或对数的大小的基本方法是构造相应的指数或对数函数,若底数不相同时转化为同底数的指数或对数,还要注意与1比较或与0比较。
(3)已知函数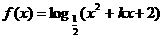 的定义域为
的定义域为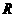 ,求
,求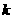 的取值范围。
的取值范围。
已知函数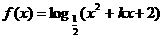 的值域为
的值域为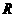 ,求
,求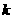 的取值范围。
的取值范围。
(1)定义:
(2)函数存在反函数的条件: ;
(3)互为反函数的定义域与值域的关系: ;
(4)求反函数的步骤:①将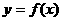 看成关于
看成关于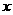 的方程,解出
的方程,解出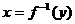 ,若有两解,要注意解的选择;②将
,若有两解,要注意解的选择;②将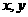 互换,得
互换,得 ;③写出反函数的定义域(即
;③写出反函数的定义域(即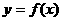 的值域)。
的值域)。
(5)互为反函数的图象间的关系: ;
(6)原函数与反函数具有相同的单调性;
(7)原函数为奇函数,则其反函数仍为奇函数;原函数为偶函数,它一定不存在反函数。
如:求下列函数的反函数: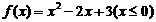 ;
;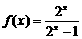 ;
;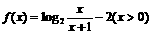
常见图像变化规律:(注意平移变化能够用向量的语言解释,和按向量平移联系起来思考)
平移变换 y=f(x)→y=f(x+a),y=f(x)+b
注意:(ⅰ)有系数,要先提取系数。如:把函数y=f(2x)经过 平移得到函数y=f(2x+4)的图象。
(ⅱ)会结合向量的平移,理解按照向量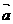 (m,n)平移的意义。
(m,n)平移的意义。
对称变换 y=f(x)→y=f(-x),关于y轴对称
y=f(x)→y=-f(x) ,关于x轴对称
y=f(x)→y=f|x|,把x轴上方的图象保留,x轴下方的图象关于x轴对称
y=f(x)→y=|f(x)|把y轴右边的图象保留,然后将y轴右边部分关于y轴对称。(注意:它是一个偶函数)
伸缩变换:y=f(x)→y=f(ωx),
y=f(x)→y=Af(ωx+φ)具体参照三角函数的图象变换。
一个重要结论:若f(a-x)=f(a+x),则函数y=f(x)的图像关于直线x=a对称;
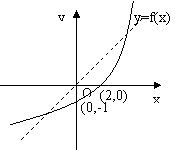 如:
如: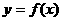 的图象如图,作出下列函数图象:
的图象如图,作出下列函数图象:
(1)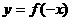 ;(2)
;(2)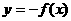 ;
;
(3)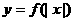 ;(4)
;(4)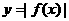 ;
;
(5)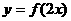 ;(6)
;(6)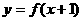 ;
;
(7)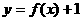 ;(8)
;(8)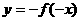 ;
;
(9) 。
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com