
题目列表(包括答案和解析)
4.汽车在行驶中,汽油平均消耗率g(即每小时的汽油消耗量,单位:L/h)与汽车行驶的平均速度v(单位:km/h)之间有函数关系:g=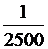 (v-50)2+5
(0<v<150).
(v-50)2+5
(0<v<150).
“汽油的使用率最高”为每千米汽油平均消耗量最小(单位:L/km),则汽油的使用率最高时,汽车速度是 (km/h).
3. 函数f(x)=log ax (a>0,a≠1),若f(x1)-f(x2)=1,则f(x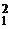 )-f(x
)-f(x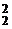 )等于
( )
)等于
( )
A.2
B.1
C.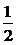 D.log a2
D.log a2
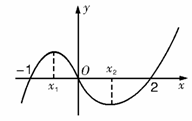
2. 如图是函数f(x)=x3+bx2+cx+d的大致图象,则x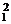 +x
+x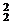 等于
( )
等于
( )
 A.
A.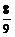
B. 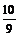
C.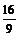
D.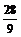
1.已知映射f:A→B,其中A=B=R,对应法则f:x→y=x2-2x+2.若对实数k∈B,在集合A中不存在原象,则k的取值范围是 ( )
A.k≤1 B.k<1 C.k≥1 D.k>1
3.已知集合A={(x,y,z)|x,y,z∈S,且x<z,y<z},S=(1,2,…,n+1}(n∈N*).
(1)当z=k+1(1≤k≤n)时,求集合A的元素个数;
(2)当x<y<z时,求集合A的元素个数;
(3)由(1)、(2)能得到一个关于自然数的恒等式,试证明你的结论.
讲解 :(1)z=k+1(1≤k≤n)时,由分步计数原理知此集合中A中有k2个元素.
(2)当x<y<z时,集合A中的元素个数等于k+1个不同的元素中取出三个不同的元素的组合数,故有?C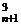 =
=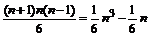 个.
个.
(3)计算A中元素个数有两种方法.
方法一:按z值分类,按(1)的结论知有12+22+32+…+n2个元素.
方法二:按x、y的大小分类:
当x<y<z时,有C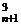 ;同理y<x<z时,有C
;同理y<x<z时,有C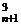 个,而x=y<z时,有C
个,而x=y<z时,有C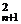 个.
个.
故2C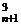 +C
+C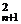 =12+22+32+…+n2,即12+22+…+n2=
=12+22+32+…+n2,即12+22+…+n2=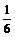 n(n+1)(2n+1).
n(n+1)(2n+1).
2.设A、B是非空集合,定义A×B={x|x∈A∪B且x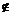 A∩B}.已知A={x|y=
A∩B}.已知A={x|y=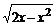 },B={y|y=2x,x>0},则A×B等于
( )
},B={y|y=2x,x>0},则A×B等于
( )
?A.[0,1)∪(2,+∞) ?B.[0,1]∪[2,+∞) ?C.[0,1] D.[0,2]
讲解:A.?∵A=[0,2],B=(1,+∞),∴A×B={x|x∈A∪B且x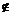 A∩B}=[0,1)∪(2,+∞).
A∩B}=[0,1)∪(2,+∞).
1.已知集合S={x||2x-1|<1},则使(S∩T)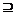 (S∪T)的集合T=
( )
(S∪T)的集合T=
( )
?A.{x|0<x<1}
B.{x|0<x<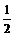 } C.{x|x<
} C.{x|x<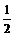 } D.{x|
} D.{x|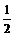 <x<1}
<x<1}
讲解:A.?由(S∩T) (S∪T)可得T=S={x||2x-1|<1}={x|0<x<1},故应选A.
(S∪T)可得T=S={x||2x-1|<1}={x|0<x<1},故应选A.
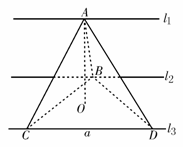
5.不共面的三条定直线l1,l2,l3互相平行,点A在l1上,点B在l2上,C、D两点在l3上,若CD=a(定值),则三棱锥A-BCD的体积 ( )
A.由A点的变化而变化 B.由B点的变化而变化
 C.有最大值,无最小值
D.为定值
C.有最大值,无最小值
D.为定值
讲解:D。如图,把△BCD当作三棱锥的底面,AO⊥面BCD于
O,∵l2∥l3,∴无论B点在l2上什么位置,△BCD的面积总
不变.又∵l2∥l3,∴l2、l3确定一个平面α,∵l1∥l2,且A不在l2、
l3确定的平面α上,∴l1平行于l2、l3确定的平面α,从而不论
A在l1的什么位置,高AO的长总不变.
又V=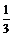 ×高×底面积,故无论A、B在什么位置时,其体积
×高×底面积,故无论A、B在什么位置时,其体积
不变.
4. 空间 (填:“存在”或“不存在”)这样的四个点A、B、C、D,使得AB=CD=8 cm,AC=BD=10cm,AD=BC=13cm.
 讲解: 要去寻找这样的点是很难叙述的.但我们可以虚拟
讲解: 要去寻找这样的点是很难叙述的.但我们可以虚拟
一些特殊的图形去模拟运动,判断结果.细看题目有四
个点,显然可以从四边形旋转所构成的三棱锥模型结构
看一下这些长度关系是否合理,来得出需要的结论.
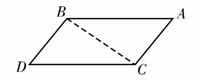
在空间中,分别以8、10、13为边长,作如图所示平面
四边形,它由△ABC和△BCD组成,公共边为BC=13 cm,AC=BD=10cm,AB=CD=8 cm,固定△ABC所在的平面,令△BCD绕着边BC旋转.显然当D位于△ABC所在的平面时,AD最大.由BC=13cm,AC=10cm,AB=8cm,可得cosBAC=-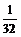 ,即可知∠BAC是钝角,故对于平行四边形(即D在平面ABC内时)ABDC,对角线AD的长小于对角线BC的长,即AD<BC=13cm.
,即可知∠BAC是钝角,故对于平行四边形(即D在平面ABC内时)ABDC,对角线AD的长小于对角线BC的长,即AD<BC=13cm.
显然,当点D不在面ABC内时都有AD<BC=13cm.因此按题目要求分布的四个点是不可能的,故知题目要求的四个点不存在.
3.已知平面α∥平面β,直线l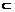 α,点P∈l,平面α、β间的距离为8,则在β内到点P的距离为10且到直线l的距离为9的点的轨迹是
( )
α,点P∈l,平面α、β间的距离为8,则在β内到点P的距离为10且到直线l的距离为9的点的轨迹是
( )
A.一个圆 B.两条直线 C.四个点 D.两个点
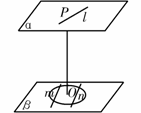 讲解:C。如图,设点P在平面β上的射影是O,则OP是平面α、β
讲解:C。如图,设点P在平面β上的射影是O,则OP是平面α、β
的公垂线段,OP=8.在β内,到点P的距离等于10的点到点O的
距离等于6,故点的集合是以O为圆心,以6为半径的圆.在β内,
到直线l的距离等于9的点的集合是两条平行直线m、n,它们到点
O的距离都等于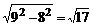 <6,所以直线m、n与这个圆均相交,
<6,所以直线m、n与这个圆均相交,
共有四个交点,因此所求的点的轨迹是四个点,故应C.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com