4.已知平面上两点M(-5，0)和N(5，0)，若直线上存在点P使|PM|-|PN|=6，则称该直线为“单曲型直线”，下列直线中是“单曲型直线”的是　　　　　 (　 )

①y=x+1;②y=2;③y=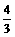x;④y=2x+1.

A.①③　　　　　 B.①②　　　　　 C.②③　　　　　 D.③④

3.A因为A构造的图形是以(1，0)为圆心，5为

半径的圆，B构造的图形是以(-1，0)为圆心，5

为半径的圆，C_t是以E(t,t)，F(t,-t),G(-t,-t),H(-t,t)为

顶点的正方形，如图所示，要使t最大，只需正方形

内接于A∩B图形，这时，由E(t,t)在(x+1)²+y²=25上

得t=3.所以满足条件的t的最大值为3.故应选A.

3.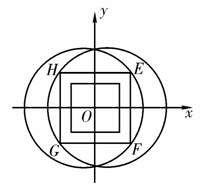设A={(x,y)|(x-1)²+y²≤25},B={(x,y)|(x+1)²+y²≤25},C_t={(x,y)||x|≤t,|y|≤t,t>0},则满足C_tA∩B时，t的最大值是　　　　　　　　 (　 )

A.3　　　　 B.4　　　　　　 C.5　　　　　 D.6

2.A　 由已知可得k=f′(-1)=3×(-1)²+2×(-1)+1=2,又由切点为(-1，2)得其切线方程为y-2=2(x+1),即y=2x+4.设此直线与抛物线切于点(x₀,2px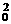),则k=4px₀=2,得px₀=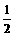,又2x₀+4=2px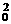,解得x₀=-4,p=-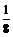,由此可得抛物线的方程为x²=-4y,其过焦点且垂直于对称轴的直线与抛物线相交得的线段长度为4，故应选A.

2．已知曲线f(x)=x³+x²+x+3在x= -1处的切线恰好与抛物线y=2px²相切，则过该抛物线的焦点且垂直于对称轴的直线与抛物线相交得的线段长度为　　　　　　 (　　 )

A.4　　　　　 B.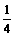　　　　　 C.8　 　　　　D.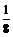

1．C方程m(x²+y²+2y+1)=(x-2y+3)²可以变形为m=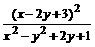,即得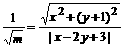,∴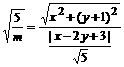其表示双曲线上一点(x,y)到定点(0,-1)与定直线x-2y+3=0之比为常数e=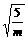,又由e>1,可得0<m<5,故应选C.

1．在直角坐标系中，若方程m(x²+y²+2y+1)=(x-2y+3)²表示的曲线是双曲线，则m的取值范围为　　　　　　　　　　　　　　　 (　　 )

A.(0，1)　　　　　 B.(1，+∞)　　　 C.(0,5)　　　 D.(5,+∞)

15. (10分)对于函数f (x)= a-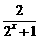(aÎR)：

(1)探索函数的单调性；(2)是否存在实数a使函数f (x)为奇函数？

14．在极坐标系中，已知点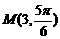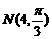，，则线段MN为长度为　　　　　 .

13．如图在杨辉三角中从上往下数共有n行，在这些数中非1的数字之和为_　　　　 _.

　　　　　　　　　 1

　　　　　　　　 1　 1

　　　　　　　 1　 2　 1

　　　　　　 1　 3　 3　 1

　　　　　 1　 4　 6　 4　 1